前两天忘发出来了,补一下QAQ
题目链接
题意简述
给定一个长度为 \(n\) 且只包含 \(\texttt{o}\) 和 \(\texttt{x}\) 的字符串 \(s\) 以及正整数 \(n\) \(m\) \(k\),令字符串 \(T=s^{m}\),求将 \(T\) 中的 \(k\) 个 \(\texttt{x}\) 变成 \(\texttt{o}\) 之后,\(T\) 中连续 \(\texttt{o}\) 的最长长度。
- \(1\leq n\leq 3\times 10^5\)
- \(1\leq m\leq 10^9\)
- 保证 \(k\) 不超过 \(T\) 中 \(\texttt{x}\) 的数量
题目分析
设 \(l,r\) 分别是修改 \(k\) 个 \(\texttt{x}\) 后最长全是 \(\texttt{o}\) 的子串的左右端点在 \(T\) 中的下标(下文默认从1开始)。
由于字符串 \(T\) 由 \(m\) 个相同的字符串 \(s\) 拼成,左端点在第一个 \(s\) 内部时一定能取到最优答案,即 \(1\leq l\leq n\)。
于是,我们只需要对每个可行的 \(l\),计算在 \(k\) 的限制内,可取到的最右边的 \(r\),答案就为 \(\max\{r-l+1\}\)。
当 \(l\) 已经确定时,我们分两种情况计算 \(r\):
-
当修改 \(k\) 个 \(\texttt{x}\) 不足以把 \(T_{l,n}\) 全变为 \(\texttt{o}\) 时,直接在 \([l,n]\) 的范围内计算 \(r\)。具体实现可以前缀和以及预处理,见参考代码。
-
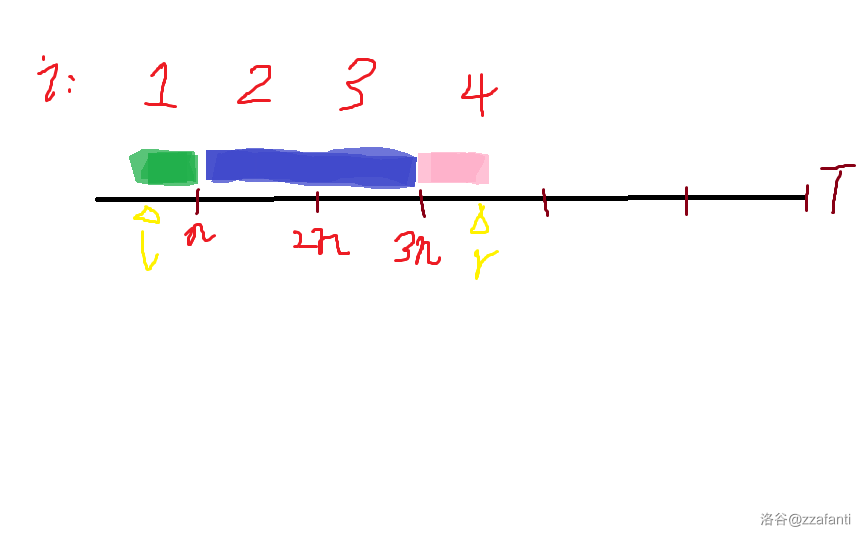
其他情况下,\(r\) 一定大于 \(n\),设 \(r\) 在第 \(i\) 段字符串 \(s\) 中,我们将最终选出的子串分为三部分:
左侧的边角块,即 \([l,n]\);
若 \(i\neq 2\),中间的整块 \([n+1,(i-1)\times n]\);
右侧的边角块,即 \([(i-1)\times n+1,r]\)。
分别对应图中绿色、蓝色、粉色部分。
对每一块分别计算即可。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N=300010;
typedef long long ll;
ll n,m,k,K,len,cst1[N],cst2[N],maxv[N],ans;
string s;
void solve(){
for(int i=1; i<=n; i++){
if(k-cst2[i]<0){
ans=max(ans,maxv[k+cst1[i-1]]-i+1);
continue;
}
ans=max(ans,n-i+1+min((k-cst2[i])/len,m-1)*n+(((1+(k-cst2[i])/len)<m)?maxv[(k-cst2[i])%len]:0));
}
cout<<ans<<endl;
}
int main(){
cin>>n>>m>>k>>s;
for(auto c:s) len+=(c=='x');
for(int i=0,cc=0; i<n; i++){
if(s[i]=='x') cc++;
cst1[i+1]=cc;
maxv[cc]=max(maxv[cc],(ll)i+1);
}
for(int cc=0,i=n-1; ~i; i--){
if(s[i]=='x') cc++;
cst2[i+1]=cc;
}
solve();
return 0;
}