基于 transformer 的编码器-解码器模型是 表征学习 和 模型架构 这两个领域多年研究成果的结晶。本文简要介绍了神经编码器-解码器模型的历史,更多背景知识,建议读者阅读由 Sebastion Ruder 撰写的这篇精彩 博文。此外,建议读者对 自注意力 (self-attention) 架构 有一个基本了解,可以阅读 Jay Alammar 的 这篇博文 复习一下原始 transformer 模型。
本文分 4 个部分:
- 背景 - 简要回顾了神经编码器-解码器模型的历史,重点关注基于 RNN 的模型。
- 编码器-解码器 - 阐述基于 transformer 的编码器-解码器模型,并阐述如何使用该模型进行推理。
- 编码器 - 阐述模型的编码器部分。
- 解码器 - 阐述模型的解码器部分。
每个部分都建立在前一部分的基础上,但也可以单独阅读。这篇分享是第三部分 编码器。
编码器
如前一节所述, 基于 transformer 的编码器将输入序列映射到上下文相关的编码序列:
\[f_{\theta_{\text{enc}}}: \mathbf{X}_{1:n} \to \mathbf{\overline{X}}_{1:n} \]仔细观察架构,基于 transformer 的编码器由许多 残差注意力模块 堆叠而成。每个编码器模块都包含一个 双向 自注意力层,其后跟着两个前馈层。这里,为简单起见,我们忽略归一化层 (normalization layer)。此外,我们不会深入讨论两个前馈层的作用,仅将其视为每个编码器模块 \({}^1\) 的输出映射层。双向自注意层将每个输入向量 \(\mathbf{x'}_j, \forall j \in {1, \ldots, n}\) 与全部输入向量 \(\mathbf{x'}_1, \ldots, \mathbf{x'}_n\) 相关联并通过该机制将每个输入向量 \(\mathbf{x'}_j\) 提炼为与其自身上下文相关的表征: \(\mathbf{x''}_j\)。因此,第一个编码器块将输入序列 \(\mathbf{X}_{1:n}\) (如下图浅绿色所示) 中的每个输入向量从 上下文无关 的向量表征转换为 上下文相关 的向量表征,后面每一个编码器模块都会进一步细化这个上下文表征,直到最后一个编码器模块输出最终的上下文相关编码 \(\mathbf{\overline{X}}_{1:n}\) (如下图深绿色所示)。
我们对 编码器如何将输入序列 "I want to buy a car EOS" 变换为上下文编码序列这一过程进行一下可视化。与基于 RNN 的编码器类似,基于 transformer 的编码器也在输入序列最后添加了一个 EOS,以提示模型输入向量序列已结束 \({}^2\)。
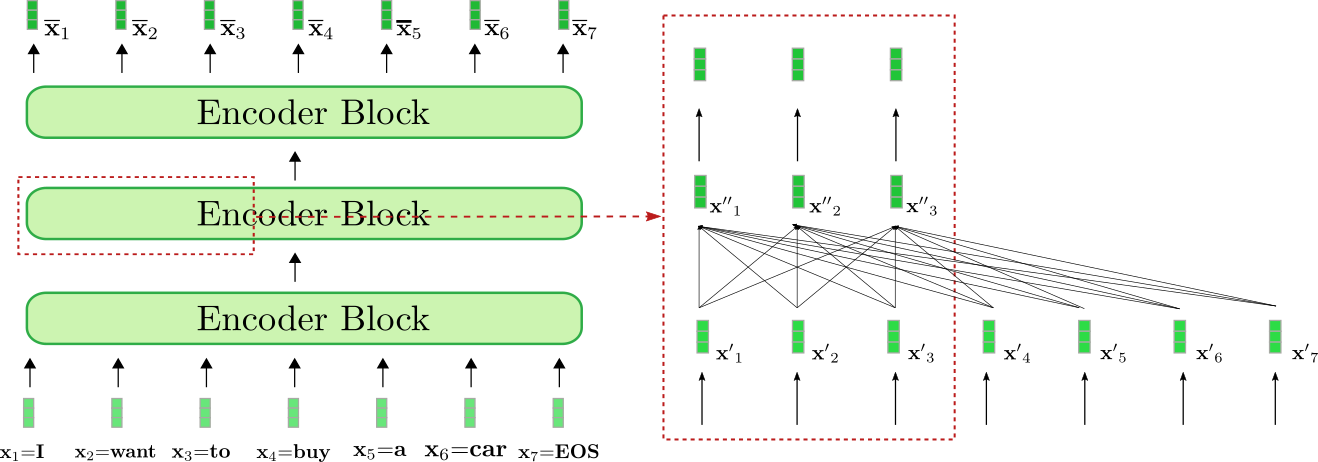
上图中的 基于 transformer 的编码器由三个编码器模块组成。我们在右侧的红框中详细列出了第二个编码器模块的前三个输入向量: \(\mathbf{x}_1\),\(\mathbf {x}_2\) 及 \(\mathbf{x}_3\)。红框下部的全连接图描述了双向自注意力机制,上面是两个前馈层。如前所述,我们主要关注双向自注意力机制。
可以看出,自注意力层的每个输出向量 \(\mathbf{x''}_i, \forall i \in {1, \ldots, 7}\) 都 直接 依赖于 所有 输入向量 \(\mathbf{x'}_1, \ldots, \mathbf{x'}_7\)。这意味着,单词 “want” 的输入向量表示 \(\mathbf{x'}_2\) 与单词 “buy” (即 \(\mathbf{x'}_4\)) 和单词 “I” (即 \(\mathbf{x'}_1\)) 直接相关。 因此,“want” 的输出向量表征, 即 \(\mathbf{x''}_2\),是一个融合了其上下文信息的更精细的表征。
我们更深入了解一下双向自注意力的工作原理。编码器模块的输入序列 \(\mathbf{X'}_{1:n}\) 中的每个输入向量 \(\mathbf{x'}_i\) 通过三个可训练的权重矩阵 \(\mathbf{W}_q\),\(\mathbf{W}_v\),\(\mathbf{W}_k\) 分别投影至 key 向量 \(\mathbf{k}_i\)、value 向量 \(\mathbf{v}_i\) 和 query 向量 \(\mathbf{q}_i\) (下图分别以橙色、蓝色和紫色表示):
请注意,对每个输入向量 \(\mathbf{x}_i (\forall i \in {i, \ldots, n}\)) 而言,其所使用的权重矩阵都是 相同 的。将每个输入向量 \(\mathbf{x}_i\) 投影到 query 、 key 和 value 向量后,将每个 query 向量 \(\mathbf{q}_j (\forall j \in {1, \ldots, n}\)) 与所有 key 向量 \(\mathbf{k}_1, \ldots, \mathbf{k}_n\) 进行比较。哪个 key 向量与 query 向量 \(\mathbf{q}_j\) 越相似,其对应的 value 向量 \(\mathbf{v}_j\) 对输出向量 \(\mathbf{x''}_j\) 的影响就越重要。更具体地说,输出向量 \(\mathbf{x''}_j\) 被定义为所有 value 向量的加权和 \(\mathbf{v}_1, \ldots, \mathbf{v}_n\) 加上输入向量 \(\mathbf{x'}_j\)。而各 value 向量的权重与 \(\mathbf{q}_j\) 和各个 key 向量 \(\mathbf{k}_1, \ldots, \mathbf{k}_n\) 之间的余弦相似度成正比,其数学公式为 \(\textbf{Softmax}(\mathbf{K}_{1:n}^\intercal \mathbf{q}_j)\),如下文的公式所示。关于自注意力层的完整描述,建议读者阅读 这篇 博文或 原始论文。
好吧,又复杂起来了。我们以上例中的一个 query 向量为例图解一下双向自注意层。为简单起见,本例中假设我们的 基于 transformer 的解码器只有一个注意力头 config.num_heads = 1 并且没有归一化层。
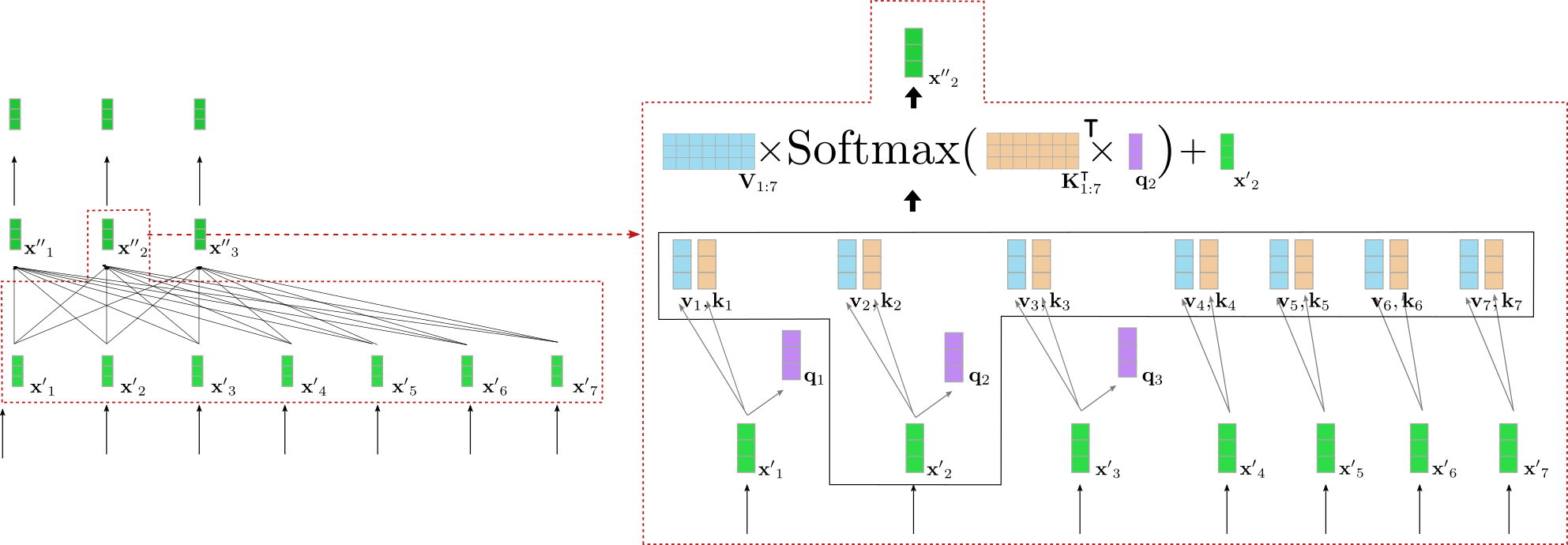
图左显示了上个例子中的第二个编码器模块,右边详细可视化了第二个输入向量 \(\mathbf{x'}_2\) 的双向自注意机制,其对应输入词为 “want”。首先将所有输入向量 \(\mathbf{x'}_1, \ldots, \mathbf{x'}_7\) 投影到它们各自的 query 向量 \(\mathbf{q}_1, \ldots, \mathbf{q}_7\) (上图中仅以紫色显示前三个 query 向量), value 向量 \(\mathbf{v}_1, \ldots, \mathbf{v}_7\) (蓝色) 和 key 向量 \(\mathbf{k}_1, \ldots, \mathbf{k}_7\) (橙色)。然后,将 query 向量 \(\mathbf{q}_2\) 与所有 key 向量的转置 ( 即 \(\mathbf{K}_{1:7}^{\intercal}\)) 相乘,随后进行 softmax 操作以产生 自注意力权重 。 自注意力权重最终与各自的 value 向量相乘,并加上输入向量 \(\mathbf{x'}_2\),最终输出单词 “want” 的上下文相关表征, 即 \(\mathbf{x''}_2\) (图右深绿色表示)。整个等式显示在图右框的上部。 \(\mathbf{K}_{1:7}^{\intercal}\) 和 \(\mathbf{q}_2\) 的相乘使得将 “want” 的向量表征与所有其他输入 (“I”,“to”,“buy”,“a”,“car”,“EOS”) 的向量表征相比较成为可能,因此自注意力权重反映出每个输入向量 \(\mathbf{x'}_j\) 对 “want” 一词的最终表征 \(\mathbf{x''}_2\) 的重要程度。
为了进一步理解双向自注意力层的含义,我们假设以下句子: “ 房子很漂亮且位于市中心,因此那儿公共交通很方便 ”。 “那儿”这个词指的是“房子”,这两个词相隔 12 个字。在基于 transformer 的编码器中,双向自注意力层运算一次,即可将“房子”的输入向量与“那儿”的输入向量相关联。相比之下,在基于 RNN 的编码器中,相距 12 个字的词将需要至少 12 个时间步的运算,这意味着在基于 RNN 的编码器中所需数学运算与距离呈线性关系。这使得基于 RNN 的编码器更难对长程上下文表征进行建模。此外,很明显,基于 transformer 的编码器比基于 RNN 的编码器-解码器模型更不容易丢失重要信息,因为编码的序列长度相对输入序列长度保持不变, 即 \(\textbf{len }(\mathbf{X}_{1:n}) = \textbf{len}(\mathbf{\overline{X}}_{1:n}) = n\),而 RNN 则会将 \(\textbf{len}((\mathbf{X}_{1:n}) = n\) 压缩到 \(\textbf{len}(\mathbf{c}) = 1\),这使得 RNN 很难有效地对输入词之间的长程依赖关系进行编码。
除了更容易学到长程依赖外,我们还可以看到 transformer 架构能够并行处理文本。从数学上讲,这是通过将自注意力机制表示为 query 、 key 和 value 的矩阵乘来完成的:
输出 \(\mathbf{X''}_{1:n} = \mathbf{x''}_1, \ldots, \mathbf{x''}_n\) 是由一系列矩阵乘计算和 softmax 操作算得,因此可以有效地并行化。请注意,在基于 RNN 的编码器模型中,隐含状态 \(\mathbf{c}\) 的计算必须按顺序进行: 先计算第一个输入向量的隐含状态 \(\mathbf{x}_1\); 然后计算第二个输入向量的隐含状态,其取决于第一个隐含向量的状态,依此类推。RNN 的顺序性阻碍了有效的并行化,并使其在现代 GPU 硬件上比基于 transformer 的编码器模型的效率低得多。
太好了,现在我们应该对:
a) 基于 transformer 的编码器模型如何有效地建模长程上下文表征,以及
b) 它们如何有效地处理长序列向量输入这两个方面有了比较好的理解了。
现在,我们写一个 MarianMT 编码器-解码器模型的编码器部分的小例子,以验证这些理论在实践中行不行得通。
\({}^1\) 关于前馈层在基于 transformer 的模型中所扮演的角色的详细解释超出了本文的范畴。Yun 等人 (2017) 的工作认为前馈层对于将每个上下文向量 \(\mathbf{x'}_i\) 映射到目标输出空间至关重要,而单靠 自注意力 层无法达成这一目的。这里请注意,每个输出词元 \(\mathbf{x'}\) 都经由相同的前馈层处理。更多详细信息,建议读者阅读论文。
\({}^2\) 我们无须将 EOS 附加到输入序列,虽然有工作表明,在很多情况下加入它可以提高性能。相反地,基于 transformer 的解码器必须把 \(\text{BOS}\) 作为第 0 个目标向量,并以之为条件预测第 1 个目标向量。
from transformers import MarianMTModel, MarianTokenizer
import torch
tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")
embeddings = model.get_input_embeddings()
# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids
# pass input_ids to encoder
encoder_hidden_states = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state
# change the input slightly and pass to encoder
input_ids_perturbed = tokenizer("I want to buy a house", return_tensors="pt").input_ids
encoder_hidden_states_perturbed = model.base_model.encoder(input_ids_perturbed, return_dict=True).last_hidden_state
# compare shape and encoding of first vector
print(f"Length of input embeddings {embeddings(input_ids).shape[1]}. Length of encoder_hidden_states {encoder_hidden_states.shape[1]}")
# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `I` equal to its perturbed version?: ", torch.allclose(encoder_hidden_states[0, 0], encoder_hidden_states_perturbed[0, 0], atol=1e-3))
输出:
Length of input embeddings 7. Length of encoder_hidden_states 7
Is encoding for `I` equal to its perturbed version?: False
我们比较一下输入词嵌入的序列长度 ( 即 embeddings(input_ids),对应于 \(\mathbf{X}_{1:n}\)) 和 encoder_hidden_states 的长度 (对应于\(\mathbf{\overline{X}}_{1:n}\))。同时,我们让编码器对单词序列 “I want to buy a car” 及其轻微改动版 “I want to buy a house” 分别执行前向操作,以检查第一个词 “I” 的输出编码在更改输入序列的最后一个单词后是否会有所不同。
不出意外,输入词嵌入和编码器输出编码的长度, 即 \(\textbf{len}(\mathbf{X}_{1:n})\) 和 \(\textbf{len }(\mathbf{\overline{X}}_{1:n})\),是相等的。同时,可以注意到当最后一个单词从 “car” 改成 “house” 后,\(\mathbf{\overline{x}}_1 = \text{“I”}\) 的编码输出向量的值也改变了。因为我们现在已经理解了双向自注意力机制,这就不足为奇了。
顺带一提, 自编码 模型 (如 BERT) 的架构与 基于 transformer 的编码器模型是完全一样的。 自编码 模型利用这种架构对开放域文本数据进行大规模自监督预训练,以便它们可以将任何单词序列映射到深度双向表征。在 Devlin 等 (2018) 的工作中,作者展示了一个预训练 BERT 模型,其顶部有一个任务相关的分类层,可以在 11 个 NLP 任务上获得 SOTA 结果。你可以从 此处 找到
标签:编码器,mathbf,transformer,解码器,向量,input,Transformers,输入 From: https://www.cnblogs.com/huggingface/p/17459315.html