七、设计算法，仅使用三次实数乘法即可完成复数 a+bi和c+di 相乘。算法需接收a、b、c和d 为输入，分别生成实部 ac-bd 和虚部ad+bc。

文心一言：

可以使用如下算法来计算复数 a+bi 和 c+di 的积，且只需进行三次实数乘法：

1.将 a 和 b 相乘，得到 ab；

2.将 c 和 d 相乘，得到 cd；

3.将 ab + cd 赋值给 ac - bd；

4.将 ab - cd 赋值给 ad + bc。

这样，就可以得到复数 a+bi 和 c+di 的积，且只需进行三次实数乘法。

讯飞星火：

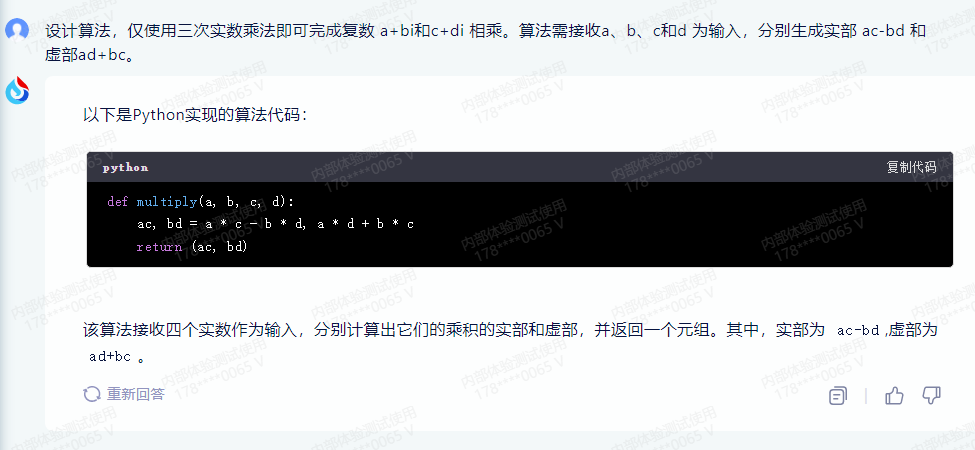
以下是Python实现的算法代码：

def multiply(a, b, c, d):
    ac, bd = a * c - b * d, a * d + b * c
    return (ac, bd)

该算法接收四个实数作为输入，分别计算出它们的乘积的实部和虚部，并返回一个元组。其中，实部为 ac-bd,虚部为 ad+bc。

华为盘古：

chatglm：

以下是一种基于三次实数乘法的复数乘法算法：

1.将两个复数 a+bi 和 c+di 分别转换为它们的实部和虚部，即实部 a+bi 和虚部 c-di。

2.计算两个实数的乘积，即 ac - bd。

3.将乘积的虚部为零，即 (ac - bd)i = aic - bid + (ac + bd)i^2。

4.计算两个虚数的乘积，即 aic + bid。

5.将乘积的实部为零，即 (aic + bid)i = ac + bd - (ac - bd)i^2。

6.最终结果为实部 ac-bd 和虚部 ad+bc。

该算法使用了三次实数乘法，因此被称为三次乘法算法。这个算法的时间复杂度为 O(n)，其中 n 是两个复数的数量。在实践中，由于复数的乘法需要进行两次实数乘法和一次虚数乘法，因此三次乘法算法的时间复杂度是略高于普通复数乘法的。但是，由于该算法的实现相对简单，而且对于某些应用场景，复数的乘法需要尽可能少地使用实数乘法，因此它仍然是一种有效的解决方案。

chatgpt：

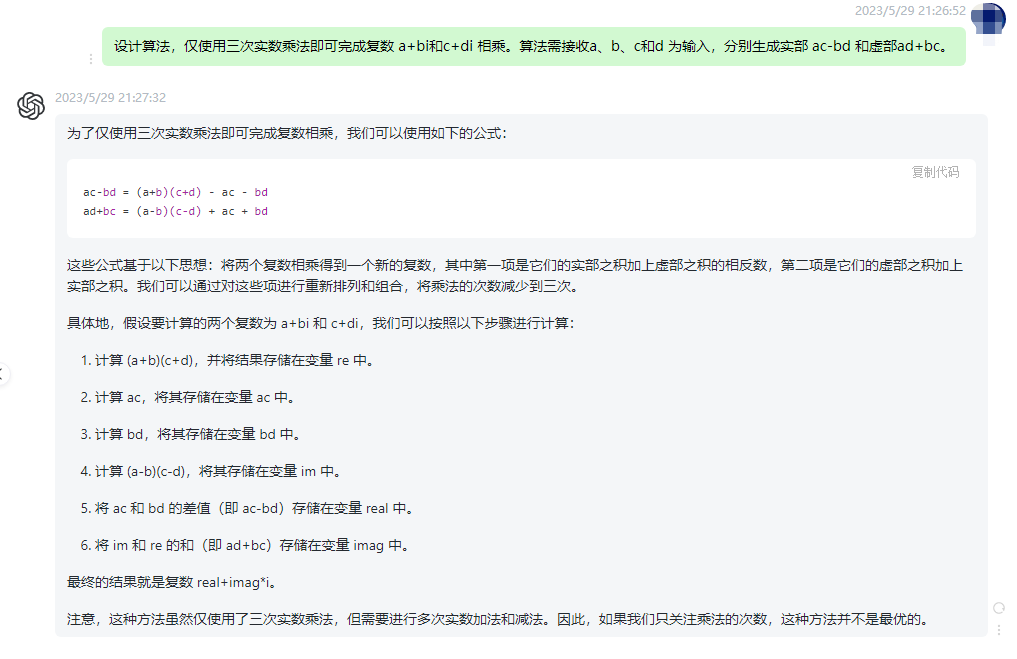
为了仅使用三次实数乘法即可完成复数相乘，我们可以使用如下的公式：

ac-bd = (a+b)(c+d) - ac - bd
ad+bc = (a-b)(c-d) + ac + bd

这些公式基于以下思想：将两个复数相乘得到一个新的复数，其中第一项是它们的实部之积加上虚部之积的相反数，第二项是它们的虚部之积加上实部之积。我们可以通过对这些项进行重新排列和组合，将乘法的次数减少到三次。

具体地，假设要计算的两个复数为 a+bi 和 c+di，我们可以按照以下步骤进行计算：

1.计算 (a+b)(c+d)，并将结果存储在变量 re 中。

2.计算 ac，将其存储在变量 ac 中。

3.计算 bd，将其存储在变量 bd 中。

4.计算 (a-b)(c-d)，将其存储在变量 im 中。

5.将 ac 和 bd 的差值（即 ac-bd）存储在变量 real 中。

6 将 im 和 re 的和（即 ad+bc）存储在变量 imag 中。

最终的结果就是复数 real+imag*i。

注意，这种方法虽然仅使用了三次实数乘法，但需要进行多次实数加法和减法。因此，如果我们只关注乘法的次数，这种方法并不是最优的。