数学专题

标识更新

\({\color{Green} \natural } {\color{Orange} \natural } {\color{Red} \natural }\)有硬核的数学或数据结构或算法

\({\color{Green} \sharp } {\color{Orange} \sharp } {\color{Red} \sharp }\)有巧妙的思维

\({\color{Orange} \flat }\)有小技巧

以上和题目本身难度无关，不同颜色只是只程度不同

20220811 XXX - 数学

CF1656D\(\surd\)

简单数论题，主要是找到\(n=\sum\limits_{i=1}^{k}(i+p)\)然后经过一些化简得到\(k(2p+k+1)=2n\)

假设\(n=2^a \times b\)若\(2^a>b\)则\(k=b\)否则\(k=a\)（根据大小性质可以推出来），然后随便判断一下就好了~

CF1603D\(\surd\)

也是比较简单的题目因为学长讲过一遍了，分情况讨论：

\(x>y\)非常好理解，就取\(x+y\)就好了，因为\(x+y<2x\)所以有\((x+y)\mod x=y\)然后\(y\mod (x+y)=y\)

\(x=y\)更容易，就用\(x\)就可以了，都等于0

\(x<y\)画个数轴就可以，设答案\(\left\lfloor \frac{n}{x}\right\rfloor=k(n\le y)\)那么把\(x\)翻个\(k\)倍，这时候\(kx\)和\(y\)之间还有一点距离，那么\(n\)恰好就在这个中点，这样它到两边的距离就相等。那么这个一段距离怎么表示？其实不难发现就是\(y\mod x\)。把这个数除2，用\(y\)减一下就得到了答案：\(y-\frac{y\mod x}{2}\)

CF1458D\(\surd \color{Red}\sharp \color{Orange}\flat\)

开始有点难度的题目了不过为什么直接是一道黑题

这题的思维非常非常巧妙，首先我们可以把1视为+1，把0视为-1，然后我们会得到一个折线图。每一次的翻转就是需要找到两个高度相同的点，然后沿着对称轴反转就可以了。

那么怎么去做呢，这里就用了一个非常神奇的想法，如果我们有两个相邻的前缀和\(pre[i],pre[i+1]\)我们就将他们之间建一条边（这里要处理一下负数的问题，其实\(+maxn\)就可以了。那我们最后的目标就是把这个图每个边都跑一边，然后尽可能地往小的走。

假如我们现在在\(k\)这个位置，我们怎么才能够合法地走到\(k-1\)，有两种情况，一种是没有到\(k+1\)的边了，另一种是到\(k-1\)至少有两条边。知道这些限制了，我们就可以贪心地找到最终的方案了。

20220812 XXX - 数学

CF1685C \(\surd\)

其实这一题和上一题的初始思路相似，仍然可以得到一个折线图。对于这一题的翻转，我们可以假设翻转的前缀和区间为\(L,R\)那么具体化的表示大概是这样的：

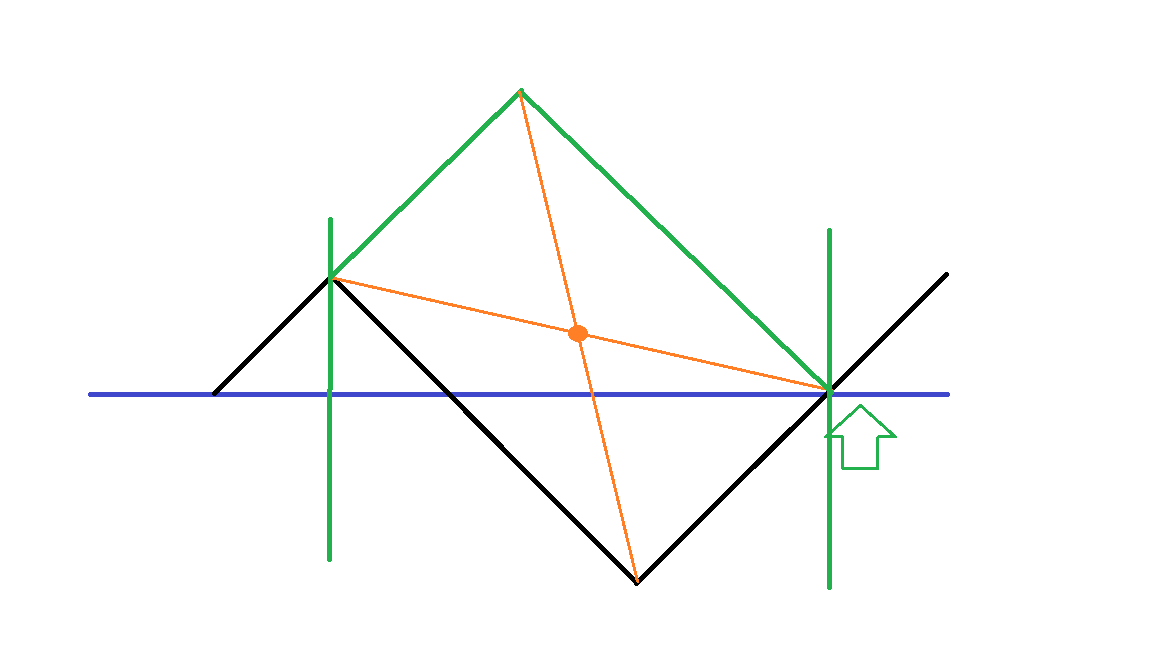
也就是说，我们翻转\(L,R\)就相当于在前缀和上的\(L-1,R\)这两个点上做图上这个操作。取中点然后全部中心对称。想清楚这个了，我们就可以想一想最优方案了。

如果没有一个点掉到0之下，我们就不用翻转。

如果允许反转两次，其实很简单。我们找到最高的点\((x_0,y_0 )\)，左右两边各操作一次，是不是就可以保证了所有点都上来了？我们只需要考虑第二高的点有没有掉下去，我们假设第二高点\((x_1,y_1 )\)在左边。最高点和原点的中点是\((\frac{x_0}{2},\frac{y_0}{2})\)所以第二高的点就会翻到\((x_0-x_1,y_0-y_1)\)又已知\(y_0>y_1\)所以这个点肯定在上面

翻转一次呢，我们找打最左边和最右边不合法的点\(l,r\)我们的翻折一定得包含这个区间，我们的目标就是要让这个区间的最高点不掉下去，那么简单推理一下，如果我们在这两个点的两侧都找最高点，那么只要满足 \(y_{maxl}+y_{maxr}\ge y_{maxmid}\)就可以做到。

也就搞定了，注意一下细节就好。

AGC002E\(\surd \color{Red}\sharp\)

又是一道妙题，这些数形结合的题目都很奇妙，可能数形结合本身就是新奇的思路。

\(nlogn\)从打到小排序之后我们先把每一个\(a_i\)放在一个网格图中，形成一个非递增的柱状图。那么我们就可以把题目看作每次操作要么就是把当前最后一行全部吃掉，要么就是把最左边的一列全部吃掉。之后我们可以把它化为一个比较熟知的博弈题，在网格纸上每次向右或者向上走，知道走到边界为止。这道题目中，边界就是所有柱形的轮廓线。这些点都是必胜点（因为都没有的可以吃了）。

接着我们考虑必胜必败点的转移，如果一个点右上两边都是必胜点，那么它就是必败点，否则就是必胜点。但是这样的复杂度是\(O(\sum a_i)\)太慢了，但是我们发现一个斜对角上的必胜必败是一样的，于是再看题解经过思考，我们只需要沿着\(y=x\)这条线走，直到到了边界前一个点，判断那一个点的胜负情况就好了。

如何判断？只许看它上面到边界的距离和右边到边界的距离。如果都是奇数就是必败点，否则必胜。解决了~

还是不得不称赞一下这些题的思维之妙。

AGC001E\(\surd\)

刚刚还想说做不出来，想了15min又感觉自己行了

对于\(C_{a+b}^{a}\)这样形式的式子，我们可以把它理解为，有一个\(n\)行\(m\)列的网格（怎么又是网格），从左下角的点走到右上角的点，每次只能往右或者往上走，这样的方案数。这个也很好证明。

那么我们可以把原式化成这样的式子，然后建立坐标系，在第三象限和第一象限放一些点，最后求第三象限的所有点到第一象限所有点的情况就可以了

对于每个二元组，我们建一个起点和一个终点，起点坐标是\((-a_i,-b_i)\)终点是\((a_i,b_i)\)，这样就可以满足一个点到另一个点的横坐标+纵坐标是\(a_i+a_j+b_i+b_j\)横坐标差是\((a_i+a_j)\)，非常好。

接着我们给每个起点设为1，然后跑\(dp\)，这里时间复杂度是\(O((2max(a_i))^2)\)，这样对于每个终点\(k\)我们相当于统计出来了\(\sum\limits_{i=1}^{n}{C_{a_i+a_k+b_i+b_k}^{a_i+a_k}}\)，我们发现这里多了两部分，一个是\(C_{2(a_k+b_k)}^{2a_k}\)也就是他自己，还有就是\(\sum\limits_{i=k+1}^{n}{C_{a_i+a_k+b_i+b_k}^{a_i+a_k}}\)也就是比它大的点，但是当我们把每一个点的结果加起来之后，我们发现只需要减去他自己，然后整体除2，就把所有不符合的情况全部剔除掉了。

这样这道题就解决了。