构造专题
标识更新
\({\color{Green} \natural } {\color{Orange} \natural } {\color{Red} \natural }\)有硬核的数学或数据结构或算法
\({\color{Green} \sharp } {\color{Orange} \sharp } {\color{Red} \sharp }\)有巧妙的思维
\({\color{Orange} \flat }\)有小技巧
以上和题目本身难度无关,不同颜色只是只程度不同
\(\surd\)切了
20220815 XXX - 构造
ARC140E \(\surd\)
从小规模的样例手玩可以逐渐看出来,这个做法像一个乘法表的样子。
但是由于\(N,M\)本身的范围比数字的个数多得多,我们考虑划分一下。首先对于一个比较小的方格进行讨论,假设\(N=9,M=9\)然后只用三个数字。
我们首先我们把\(9\times9\)的格子划分成九个\(3\times3\)的格子,然后对于每个格子我们用3个数字填充,因为我们要尽量让一列和一行重复的比较少,不然对于之后的选择非常不友好,将具体一点,就比如说我们整一个
\[\begin{pmatrix} 0 & 0 & 0\\ 1 & 1 & 1\\ 2 & 2 & 2 \end{pmatrix} \]这本身是合法的,但是利用性不高,不适合重复使用。这里我们用类似数独的做法填出来三个方案:
\[Block_0=\begin{pmatrix} 0 & 1 & 2\\ 1 & 2 & 0\\ 2 & 0 & 1 \end{pmatrix} Block_1=\begin{pmatrix} 1 & 2 & 0\\ 2 & 0 & 1\\ 0 & 1 & 2 \end{pmatrix} Block_2=\begin{pmatrix} 2 & 0 & 1\\ 0 & 1 & 2\\ 1 & 2 & 0 \end{pmatrix} \]三个。不难发现这些是不断轮换的,我们以行来看,就是\(0,1,2\)不断的交替,那么其实我们确定了这是那一个\(Block\)的哪一行,我们就知道是什么数字了,具体来说\(Block_k[i][j]=(i+j+k)\mod p\)
感性的理解就是\(k\)的编号表示第0行第0个数就是\(k\)那么循环一下就i可以得到所有的数字了。
之后把这些方块填入大矩形当中,我们很快发现直接轮换填是不可行的,(虽然这种方法可以满足四个点出现在1、2格的大格子中没问题,但是出现在4个格子中不可行)这里还是得经过一定的手动模拟(其实从正解推回来结论是成立的,但是我现在也无法说明一个完全准确的为什么要这样构造的原因),我们想到乘法表的形式,对于每一行我们我们填横纵坐标相乘模p的余数。这样我们就可以推出来\(ans[i][j]=\left \lfloor \dfrac{i}{p} \right \rfloor \times \left \lfloor \dfrac{j}{p} \right \rfloor \mod p+i\mod p+j\mod p\)
这里写这么多取模是为了从本质上理解,除以\(p\)向下取整就可以求出来这是哪一个小方块,之后算出来这个方块具体的\(i,j\)的位置是什么就可以了,这个把模弄到一起就是题解的式子了。
P9118\(\surd\color{green}\natural\color{Orange}\flat\)
大致思路讲一下
最粗糙的想法就是\(O(4n)\),怎么做就不用说了。
稍微想一下可以知道,我们利用一下交换的操作,可以让一个点一直探索,另一个就呆在原地,每到一个新的点就交换一下,这样就实现了\(O(3n)\)
那么我们发现这样做有亏损,就是其中一给点一直呆在一个点,没有贡献,那我们就考虑让两个点同时走。
同时走的具体操作如何?我们想一个点一定会经过\(root->leaf->root\)这样的过程,那么我们发现后半段其实是浪费的,所以我们就这样想,让一个点dfs到一个点之后和另一个点交换,让另一个点向上回溯,直到回溯到一个它走过的点或者是一个还没有被\(dfs\)过的分支。两边同时进行。
首先我们生成一棵树,从哪里开始呢?不难想到,从重心开始肯定最优的,因为它可以保证\(2\times min(siz[a],siz[b]) \le max(siz[a],siz[b])\)这样理论的最劣情况就是\(O(\left \lfloor \dfrac{8}{3}n \right \rfloor)\)的
不过代码本身的实现还是比较长的。
可算是改过了,说一些细节:
- 首先在建树的时候最好使用类似并查集的形式,简单一些而且好像dfs会被卡一个点,不知道是不是我建错了,但是生成树用并查集还是挺不错的
- 在分配方面有一个坑的,我们需要尽量的平均分配给两个人,虽然看一些小的样例感受不出来随便走和不随便走的区别,但是这玩意卡得挺死的。把重心的子树排个序,然后\(O(n)\)整一个贪心就好。(虽然好像最好的解是用\(dp\)但是时间复杂度不允许。
- 最后在实现的部分,可能这样的思路比较清晰:找到这两个分别要去的节点,先去那个节点,然后全部\(dfs\)一遍,之后回来的时候标记一下表示回来了。在大while循环的时候就就把两个点的过程一起做再加上\(swap\)
20220816 XXX - 构造
CF1586I\(\surd\color{Red}\sharp\)
极好的一道题目,思维量非常高,没啥算法的东西,只用模拟的知识就能做出来,但是想的过程确实强
我们先手玩一下,从左下角入手,相邻的两个一定和它不一样,之后沿着对角线向上,会发现出现的颜色一定是交替进行的。对于另一个对角线我们进行同样的操作,会得到同样的性质。到这里我们就容易发现,如果\(n\)是奇数,就一定不成立,因为两个对角线就矛盾了。
之后我们看\((1,3)\)这个格子(此处是以左下角的格子建立的坐标系的),由于\((1,1)=(1,2)\)所以\((1,3)=(3,1)\ne(2,2)\),又因为\((1,2)\ne(2,3)\)所以\((1,3)=(1,4)\)同理,\((3,1)=(4,1)\)。这个结论在左下角和右上角都是适应的。对于两个长的对角线我们发现这里也必须是交替进行的,因为它和之前的两个对角线之间相互限制。
是不是发现一些规律?在图上画出来,会发现确定一个点,就会有一个边界类似六边形的部分被一起确定下来比如\(n=6\)的时候,我们就会画出来:
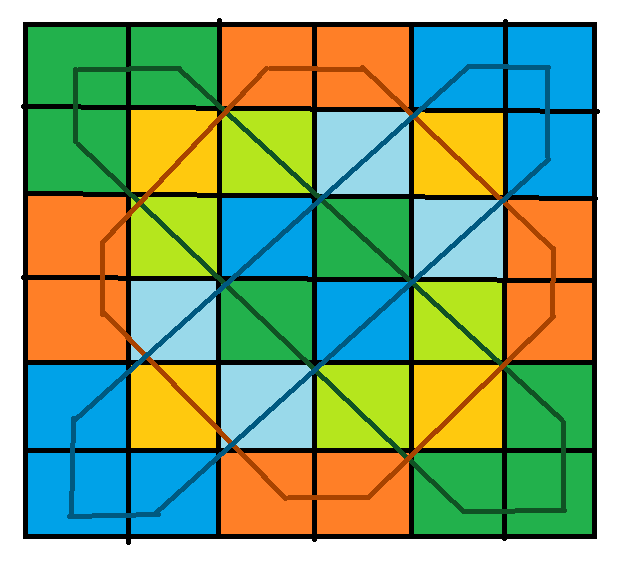
【其实这道题题解写的就非常好,在这里
里面图片和文字说明都非常详细,相信可以直接看懂】
这里我们就发现了本题最重要的性质,就是其实这个图是分成很多个这种环形的,彼此之间是相互不影响的,但是内部只要确定了一个点就可以推算出来所有的点。那么之后判断答案就很容易了:
如果奇数就是\(NONE\)
否则如果偶数中两个点在同一环形内部但之间又矛盾,也是\(NONE\)
如果输入当中有一个环形内部没有任何规定的点,就是\(MULTIPLE\)
最后如果每个环形当中都有不矛盾的点,就是\(UNIQUE\)模拟一下就可以得到答案了。
20220817 XX - 构造
ARC099F
没有太想明白,晚点来看
AGC004E\(\surd \color{Green}\sharp\)
比较巧妙的一个转化就是因为机器人太多了,我们直接让全部机器人一起行动是不太现实的,所以我们让唯一的出口h额墙壁一起来行动。
出口移动我们会发现一些有意思的地方,出口的移动范围是一个矩形,J假设以它的起点开始,到每个边的距离分别是\((l,r,u,d)\)。每次往一个方向走的时候,另一个方向的墙壁会炸掉一些机器人。那我们根据所有墙壁移动的空间可以在图的中央围成一个封闭的空间,这个空间是起点可能走到的位置
官方题解给了一个很好的图
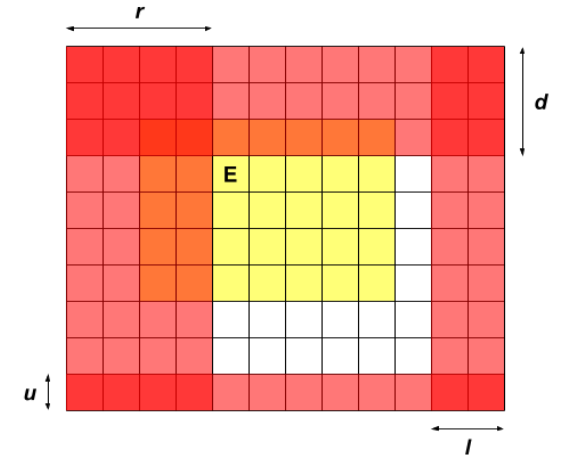
现在假设我们知道起点走黄色矩形的时候的最优值,然后我们考虑往白色的部分进发,我们记现在的最优值是\(dp[l][r][u][d]\),那么\(dp[l][r+1][u][d]=max(dp[l][r+1][u][d],sum_{white})\)最后的和指的是白色的那一块区域的机器人数量,注意不能被红色的部分覆盖。
这个做法非常好,但是我们漏了一个小小的判断,我们想此时往上进发可不可以?答案是否定的,因为上面已经是红的了,所以我们发现必须要满足\(l+r<startx-1\)的时候才可以向上走,其他情况同理。
【这里插一句,或许你我会感到疑惑,为什么红色和白色交接的位置不去算?因为我们可以知道,我们走了黄色区域,红色的区域的机器人一定爆掉了,我们是吃不到的。那可能又会问到,那我走黄色区域的时候把那里保留一下?没错,但是再仔细想想,这样就有其他的状态转移过来了~】
这样我们就有一个\(O(n^4)\)的\(dp\)做法了,这是很不错的。很容看出来\(sum\)用前缀和处理一下就搞定了。
20220925 SS - 构造
CF743C \(\surd\)
基本没有技术含量
特判\(n=1\)情况
其他情况输出\(n,n+1,n(n+1)\)即可
CF476D \(\surd\)
同样简单,很容易发现四个当中只能有一个是偶数,且不能有任何倍数关系
那我们可以很轻易地构造出来\(\left\{ 6k+1,6k+2,6k+3,6k+5 \right \}\)
CF715D\(\surd \color{Orange}\sharp\)
官方题解很好,只是画的图有点丑。
简单来说我们把\(n\)化为六进制的形式,接着我们考虑构造一个\(3\times 3\)的方格来控制

我们很容易发现,只要外围我们维护一圈1,我们可以不断实现出\(k\)到\(6k+i (i\in [0,5])\)的飞跃。也就是中间打开一些位置,如打开这张图的\((1,4),(2,4)\)之间的限制打开,我们就可以实现出来\(6k+1\)
我们只需要通过这样的不断嵌套,就可以实现一个六进制的数字了!
可能会想到,为什么不用\(2\times 2\)的方格呢?很简单,因为这只能够实现\(2k+i\),这是很不优秀的,因为题目要求在\(50\times 50\)的限制,简单算一下就发现不太行
标签:surd,专题,一个点,color,构造,pmatrix,sharp,我们 From: https://www.cnblogs.com/Jryno1-blog/p/16728163.html