前言

以下内容大多摘抄自董晓算法

前置芝士

相关定义

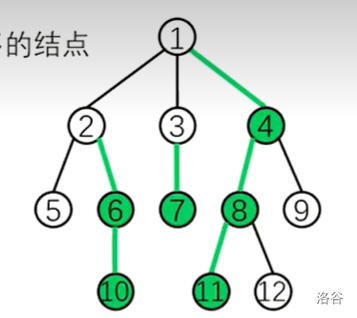
重儿子：父节点的所有儿子中子树结点数目最多的结点

轻儿子：父节点中除了重儿子之外的儿子

重边：父结点和重儿子连成的边

轻边：父结点和轻儿子连成的边

重链：由多条重边连接而成的路径

前置数组含义

\(fa[u]\):存 \(u\) 的父节点

\(dep[u]\):存 \(u\) 的深度

\(son[u]\):存 \(u\) 的重儿子

\(size[u]\):存以 \(u\) 为根的子树的结点数

\(top[u]\):存 \(u\) 所在的重链的顶点(深度最小的那个点)

\(id[u]\):存 \(u\) 剖分后的新编号

\(wt[tot]\):存新编号在树中所对应结点的权值。

相关性质

• 整棵树会被剖分成若干条重链

• 轻儿子一定是每条重链的顶点

• 任意一条路径被切分成不超过 \(logn\) 条链

树链剖分可以解决的问题

树链剖分可以解决树上的一些链操作，比如将 \(u\) 到 \(v\) 路径上的权值做一些操作、对 \(u\) 的子树做一些操作、求 LCA 等一些比较繁琐的操作。

算法原理

树链剖分是基于 dfs 来实现的，原理比较简单。

如果是处理 \(u\) 的子树方面的问题，那么由于 dfs 的性质，一个子树内的 dfs 顺序是连续的，所以我们可以很简单的进行维护；

如果要维护一条链呢？我们并不能保证这条链上结点是连续的，那就退而求其次。由树剖的性质可得，任意一条路径会被切分成不超过 \(logn\) 条链，因此我们分别维护每一条链就行了。

怎么快速地维护呢？线段树/oh。因为我们要维护每一条重链，所以我们在 dfs 的时候优先 dfs 重儿子，使得一条链上的结点的 dfs 序连续,这样我们就能把树上的每一条链转换为一个一个的小区间，而每一个小区间就可以线段树进行维护了。

总之，树链剖分就是把树转换成一个序列，再利用线段树进行维护，就能高效的处理树上问题了。

一般的时间复杂度是 \(O(nlog^2n)\) 线段树的 \(log\) 和树剖跳链的 \(log\)

算法流程

一.预处理

第一次 dfs ，搞出 \(fa,dep,size,son\) 数组(为了剖分做准备)

第二次 dfs ，搞出 \(top,id,wt\) 数组

il void dfs1(int x,int f)
{
	dep[x] = dep[f] + 1 , fa[x] = f , siz[x] = 1;
	for(re int i=head[x];i;i=edge[i].next)
	{
		int y = edge[i].v;
		if(y == f) continue;
		dfs1(y,x);
		siz[x] += siz[y];
		if(siz[son[x]] < siz[y]) son[x] = y;
	}
}

il void dfs2(int x,int topf)
{
	id[x] = ++tot , wt[tot] = w[x] , top[x] = topf;
	if(!son[x]) return ;
	dfs2(son[x],topf);
	for(re int i=head[x];i;i=edge[i].next)
	{
		int y = edge[i].v;
		if(y == fa[x] || y == son[x]) continue;
		dfs2(y,y);
	}
}

利用新 \(id\) 和 \(wt\) 建树

il void build(int p,int l,int r)
{
	if(l == r)
	{
		tree[p] = wt[l] % mod;
		return ;
	}
	int mid = (l+r) >> 1;
	build(lc,l,mid);
	build(rc,mid+1,r);
	tree[p] = (tree[lc] + tree[rc]) % mod;
}

二.查询

1.查询树从 \(x\) 到 \(y\) 结点最短路径上所有节点值的和：

il int Query(int nl,int nr,int l,int r,int p)
{
	int res = 0;
	if(l >= nl && r <= nr) return tree[p] % mod;
	push_down(p,l,r);
	int mid = (l+r) >> 1;
	if(nl <= mid) res += Query(nl,nr,l,mid,lc);
	if(nr > mid) res += Query(nl,nr,mid+1,r,rc);
	return res % mod;
}
      
il int Query_way(int x,int y)
{
	int res = 0;
	while(top[x] != top[y])
	{//不断的往上跳
		if(dep[top[x]] < dep[top[y]]) swap(x,y);
		res = (res + Query(id[top[x]],id[x],1,n,1)) % mod;
		x = fa[top[x]];//这条链处理完了，跳到另一条链上
	}
	if(dep[x] > dep[y]) swap(x,y);
	res = (res + Query(id[x],id[y],1,n,1)) % mod;//x，y在同一条链上了，再把它俩之间的部分处理一下
	return res % mod;
}

2.将 \(x\) 到 \(y\) 结点上的权值增加 \(k\)

il void Modify(int nl,int nr,int l,int r,int p,int k)
{
	if(l >= nl && r <= nr)
	{
		tag[p] = (tag[p]+k) % mod;
		tree[p] = (tree[p]+(r-l+1)*k) % mod;
		return ;
	}
	push_down(p,l,r);
	int mid = (l+r) >> 1;
	if(nl <= mid) Modify(nl,nr,l,mid,lc,k);
	if(nr > mid) Modify(nl,nr,mid+1,r,rc,k);
	tree[p] = (tree[lc] + tree[rc]) % mod;
}//其实这部分就是普通的线段树
      
 il void Modify_way(int x,int y,int k)
{
	while(top[x] != top[y])
	{
		if(dep[top[x]] < dep[top[y]]) swap(x,y);
		Modify(id[top[x]],id[x],1,n,1,k);
		x = fa[top[x]];
	}//原理其实同 Query_way 相似
	if(dep[x] > dep[y]) swap(x,y);
	Modify(id[x],id[y],1,n,1,k);
}

说白了，树链剖分只是充当了一个划分序列的角色，真正的大头还是线段树。

3.查询 \(u\) 及其子树的权值和

因为我们知道，一个点子树的 dfs 序是连续的，因此剖分后的区间的左端点就是 \(id[u]\) ，右端点就是 \(id[u]+siz[u]-1\) ，我们直接 Query 即可

Query(id[x],id[x]+siz[x]-1,1,n,1)

4.将 \(u\) 及其子树的权值加 \(k\)

原理同上

Modify(id[x],id[x]+siz[x]-1,1,n,1,k);

总结

树链剖分其实只是一个工具，真正树剖题变化的还是你的线段树想维护什么:区间最大值，区间和，区间变化，树剖+二分等等很多的变化形式，做题多了就能见识到了，上文所提及的都是最基础的一部分。