可持续化线段树

前言：
“这个数据结构是属于比较抽象的一类。并且代码实现比较繁琐复杂。”
别人都这么说，我却觉得挺好理解、也挺好写的（可能是因为我曾经与多道线段树毒瘤题抗争多次）。
为了避免以后我突然脑子抽了不记得了，可以拿出来看看。所以写下这篇笔记，希望也能帮到大家。

建议：带上一个清晰的脑子（草稿纸和笔是没有用的，因为理解过程中会用三维的叠加操作）。

注：本篇文章是我这个小蒟蒻写的，真正的dalao请看个玩笑便好，不必争论对错（但是欢迎指出文章存在的小错误）。

什么是可持续化线段树

可持续化线段树，就是一种能保存历史版本信息的线段树。
“可持续化”——可以返回之前的某个状态，并在该基础上进行修改。
可持续化线段树就是这样的一种结构。

为什么要用可持续化线段树

我们先考虑一个一般场景：

此时你要实现一个可持久化的线段树，你会怎么做？

一般人想到的、最朴素的做法就是每一次操作都新建一棵线段树。

但是无论从空间还是时间上看，这种算法都是一种非常差的算法。

仔细思考：

我们每次更新肯定不会一整棵树进行修改，那么我们每次都要新建一棵树吗？

显然不用。所以我们无需重新建树。

什么是主席树

主席树是可持续化线段树的一种。

因为这种结构由黄嘉泰同学发明，而名字拼音缩写又恰好与曾经的一位提出科学发展观的主席的名字拼音缩写相同，所以称为主席树。

主席树是以时间轴将（不同时刻状态的线段树的）根节点串起来的多层的权值线段树。
每一层的根节点都代表一个历史时刻的入口，每一层可以共用之前层的节点。

为什么要使用主席树

主席树最初发明时，是为了解决区间第\(k\)小的问题。

主席树

主席树是权值线段树（上文有提），那么插入数据的时候，我们将得到一条链。

例如我们数组元素的值域在\([1,10^3]\)之间，插入的第一个数据是\(100\)，那通过“往左往右”（类似分治）的方法就可以找到代表\(100\)的叶子节点。
详见图一：

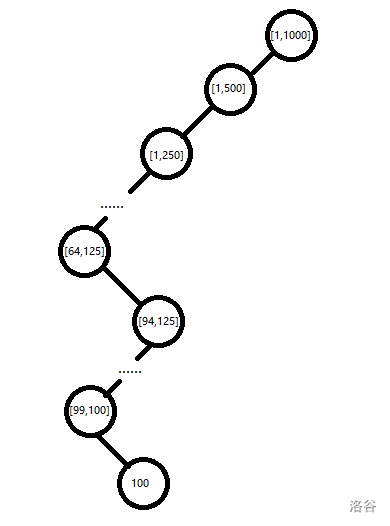
而类似的，我们在下一次插入新数据的时候，也会得到一条从根节点到叶子结点的一条链。
当插入\(666\)时，如图二：

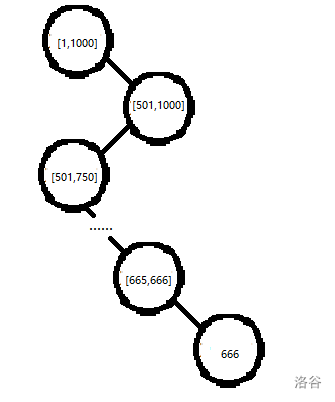
注意！

此时我们已经插入了两次数据，那么我们在插入第二次数据的同时，也要将第二棵树某些节点连向第一棵树“已开拓的边”。
也就是说，插入第二次数据后，我们得到的线段树不会仅仅是上图的一条链，而是如图三所示的一棵树：

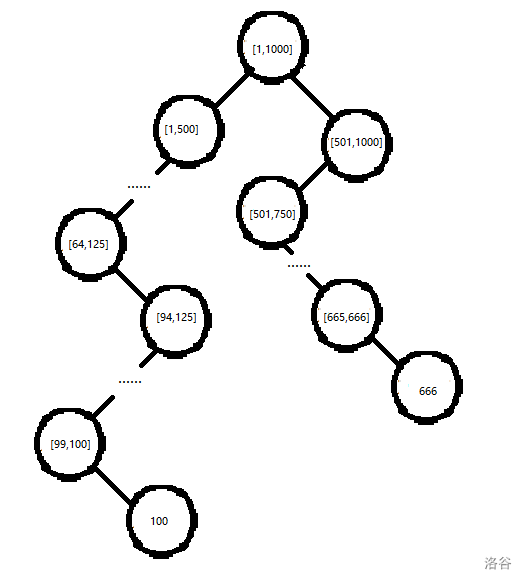
一个结论

那么我们可以将主席树简单理解成一个可以排开竖着放小玻璃片的暗箱。然后每一次插入数据，可以理解成每次放一张小玻璃片（按插入时间顺序依次有序放），而小玻璃片上面印着从根到叶子节点的链的图案。

当我们想查询第\(n\)次的线段树状态时，可以理解成在第\(n\)张与第\(n+1\)张玻璃片之间放一个不透光的白布；然后用一束光从第一张玻璃片打过去，在白布上呈现的图案，就是第\(n\)次历史时刻的图案。

如图四：

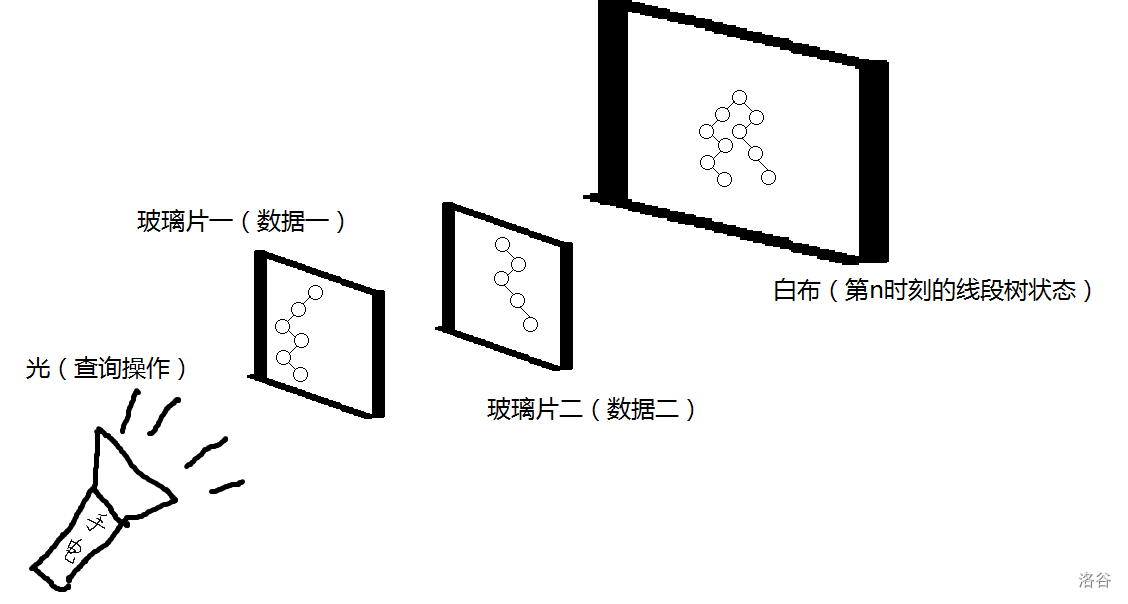
那么主席树的实现原理也就搞清楚了，可以挂代码了。

主席树代码实现

插入操作

code:

#define ll long long
void update(ll r)
{
    tr[r].sz=tr[tr[r].lc].sz+tr[tr[r].rc].sz;
}
void ins(ll &rt,ll lst,ll l,ll r,ll val)
{
    rt=++tot;
    tr[rt]=tr[lst];
    if(l==r)
        tr[rt].sz++;
    else
    {
        ll mid=(l+r)>>1;
        if(val<=mid)
            ins(tr[rt].lc,tr[lst].lc,l,mid,val);
        else
            ins(tr[rt].rc,tr[lst].rc,mid+1,r,val);
        update(rt);
    }
}

查询操作

code:

ll query(ll r1,ll r2,ll l,ll r,ll k)
{
    if(l==r)
        return l;
    ll lc1=tr[r1].lc,lc2=tr[r2].lc;
    ll mid=(l+r)>>1;
    ll tmp=tr[lc2].sz-tr[lc1].sz;
    if(tmp>=k)
        return query(lc1,lc2,l,mid,k);
    return query(tr[r1].rc,tr[r2].rc,mid+1,r,k-tmp);
}

main函数

code:

const ll INF=1e3;
#define rp(i,o,p) for(ll i=o;i<=p;++i)
int main()
{
    scanf("%lld%lld",&n,&m);
    rp(i,1,n)
    {
        scanf("%lld",&a[i]);
        ins(rts[i],rts[i-1],1,INF,a[i]);
    }
    rp(i,1,m)
    {
        ll x,y,z;
        scanf("%lld%lld%lld",&x,&y,&z);
        printf("%lld\n",query(rts[x-1],rts[y],1,INF,z));
    }
    return 0;
}

板题&后记

主席树还是挺好学的，主要是要抽象出那个模型就好了。
本片题解写得比较仓促，还有一些没有写到（下次再补了）。

挂一个板子吧。

（不要问我为什么没有链接，因为luogu的板题还没做，只做了校内OJ的题）

题意：给定一个长度为\(n\)的序列，\(m\)个询问，每个询问的形式为：\(l，r，k\)表示在\([l,r]\)间中的第\(k\)小元素。

数据范围：\((n\leq 10^5，m\leq 10^5，1\leq l\leq r\leq n， 1\leq k\leq r-l+1，1\leq a_i\leq 10^9)\)

code:

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define rp(i,o,p) for(ll i=o;i<=p;++i)
#define pr(i,o,p) for(ll i=o;i>=p;--i)

const ll MAXN=1e5+5,INF=1e9;

ll n,m,tot;
ll a[MAXN];
ll rts[MAXN];
struct TREE
{
    ll lc,rc,sz;
}tr[MAXN<<2];

void update(ll r)
{
    tr[r].sz=tr[tr[r].lc].sz+tr[tr[r].rc].sz;
}

void ins(ll &rt,ll lst,ll l,ll r,ll val)
{
    rt=++tot;
    tr[rt]=tr[lst];
    if(l==r)
        tr[rt].sz++;
    else
    {
        ll mid=(l+r)>>1;
        if(val<=mid)
            ins(tr[rt].lc,tr[lst].lc,l,mid,val);
        else
            ins(tr[rt].rc,tr[lst].rc,mid+1,r,val);
        update(rt);
    }
}

ll query(ll r1,ll r2,ll l,ll r,ll k)
{
    if(l==r)
        return l;
    ll lc1=tr[r1].lc,lc2=tr[r2].lc;
    ll mid=(l+r)>>1;
    ll tmp=tr[lc2].sz-tr[lc1].sz;
    if(tmp>=k)
        return query(lc1,lc2,l,mid,k);
    return query(tr[r1].rc,tr[r2].rc,mid+1,r,k-tmp);
}

int main()
{
    scanf("%lld%lld",&n,&m);
    rp(i,1,n)
    {
        scanf("%lld",&a[i]);
        ins(rts[i],rts[i-1],1,INF,a[i]);
    }
    rp(i,1,m)
    {
        ll x,y,z;
        scanf("%lld%lld%lld",&x,&y,&z);
        printf("%lld\n",query(rts[x-1],rts[y],1,INF,z));
    }
    return 0;
}