滑动窗口 单调队列

描述

给一个长度为 N 的数组，一个长为 K 的滑动窗体从最左端移至最右端，你只能看到窗口中的 K 个数，每次窗体向右移动一位，如下图：

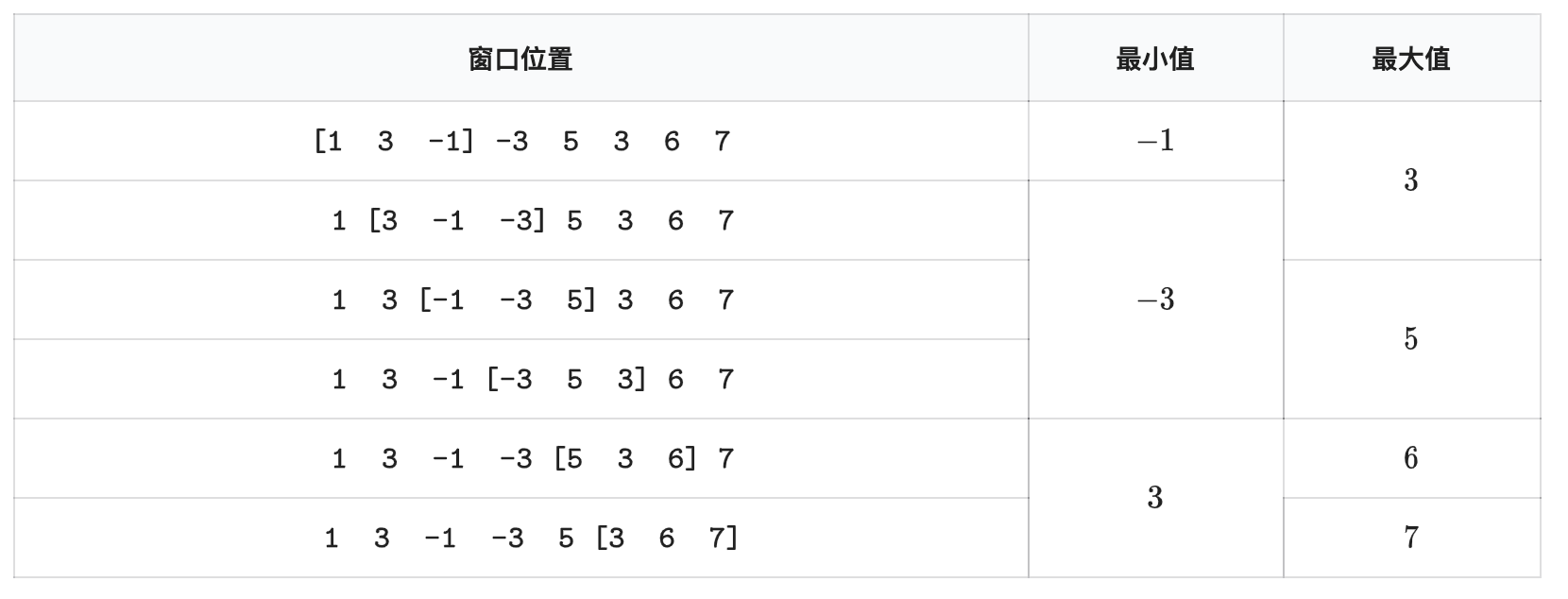
你的任务是找出窗体在各个位置时的最大值和最小值。

输入

第 1 行：两个整数 N 和 K；

第 2 行：N 个整数，表示数组的 N 个元素(≤2×10⁹ )；

对于 20% 的数据，K≤N≤1000；

对于 50% 的数据，K≤N≤10⁵ ；

对于 100% 的数据，K≤N≤10⁶ 。

输出

第一行为滑动窗口从左向右移动到每个位置时的最小值，每个数之间用一个空格分开；

第二行为滑动窗口从左向右移动到每个位置时的最大值，每个数之间用一个空格分开。

样例输入

8 3
1 3 -1 -3 5 3 6 7

样例输出

-1 -3 -3 -3 3 3
3 3 5 5 6 7

思路：

滑动窗口算法是一种非常有用的算法，可以用于在序列中找到子序列的最大值或最小值。在给定的代码示例中，我们使用一个双端队列来维护窗口，并在每个步骤中执行以下操作：

1. 如果队列中的第一个元素已经超出了窗口的范围，则将其从队列中删除。
2. 删除队列中所有小于当前元素的元素。
3. 将当前元素添加到队列的末尾。
4. 如果我们已经处理了k个元素，则输出队列中的第一个元素，即当前窗口的最大值。

如果我们想要找到当前窗口的最小值，我们只需要将第2步中的“大于等于”改为“小于等于”。下面是一个示例程序，它找到一个序列中长度为k的子序列的最大值和最小值：

#include <iostream>
#include <deque>

using namespace std;
const int N = 1e6+10;
int arr[N],n,k,cnt,maxx[N],minn[N];
void printKMaxAndMin(int arr[], int n, int k){
    deque<int> max_dq, min_dq;
    for(int i=0;i<n;i++){
        if(!max_dq.empty() && max_dq.front() == i-k)
            max_dq.pop_front();
        if(!min_dq.empty() && min_dq.front() == i-k)
            min_dq.pop_front();
        while(!max_dq.empty() && arr[i]>=arr[max_dq.back()])
            max_dq.pop_back();
        while(!min_dq.empty() && arr[i]<=arr[min_dq.back()])
            min_dq.pop_back();
        max_dq.push_back(i);
        min_dq.push_back(i);
        if(i>=k-1){
            maxx[++cnt] = max_dq.front();
            minn[cnt] = min_dq.front();
            //cout<<arr[max_dq.front()]<<" ";
            //cout<<arr[min_dq.front()]<<" ";
        }
    }
    //cout<<endl;
}

int main(){
    cin>>n>>k;
    for(int i=0;i<n;i++)scanf("%d",&arr[i]);
    printKMaxAndMin(arr, n, k);
    for(int i=1;i<=cnt;i++)
    {
        cout<<arr[minn[i]];
        if(i!=cnt)cout<<" ";
        else cout<<endl;
    }
    for(int i=1;i<=cnt;i++)
    {
        cout<<arr[maxx[i]];
        if(i!=cnt)cout<<" ";
        else cout<<endl;
    }
    return 0;
}