
反三角函数是基本初等函数的重要组成部分,但似乎又是许多人常问的主体之一。为了方便理解和查询,本文总结了以下内容:
- 常见的六种三角函数对应的反三角函数的定义、定义域、值域,并给出对应三角形图示汇总、对应图象汇总
- 利用反函数求导法则完成了上述所有反三角函数的导数公式的推导,并详细总结了其值域、定义域等内容
本文内容也可作为备忘资料以便查阅使用。
一、常用三角函数与反三角函数
- 常见的六种三角函数可以分别由以下六种三角形表示
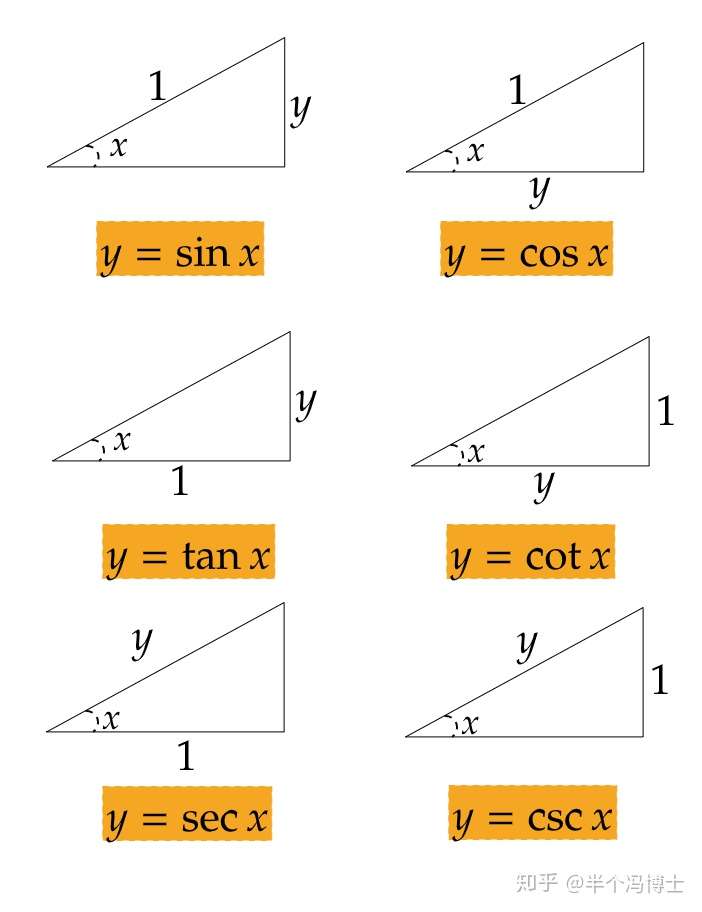
图1.三角函数及其对应三角形
- 反三角函数是三角函数的反函数。若将上图中所有x,y 调换位置则得到反三角函数的图示:
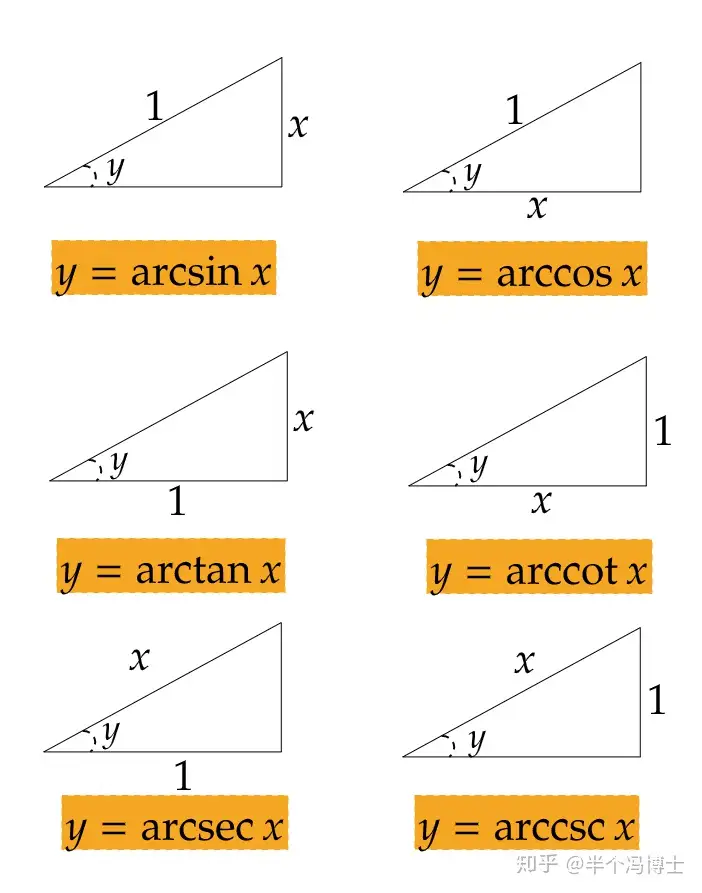
图2.反三角函数及其对应三角形
上述反三角函数的图象如下图所示:
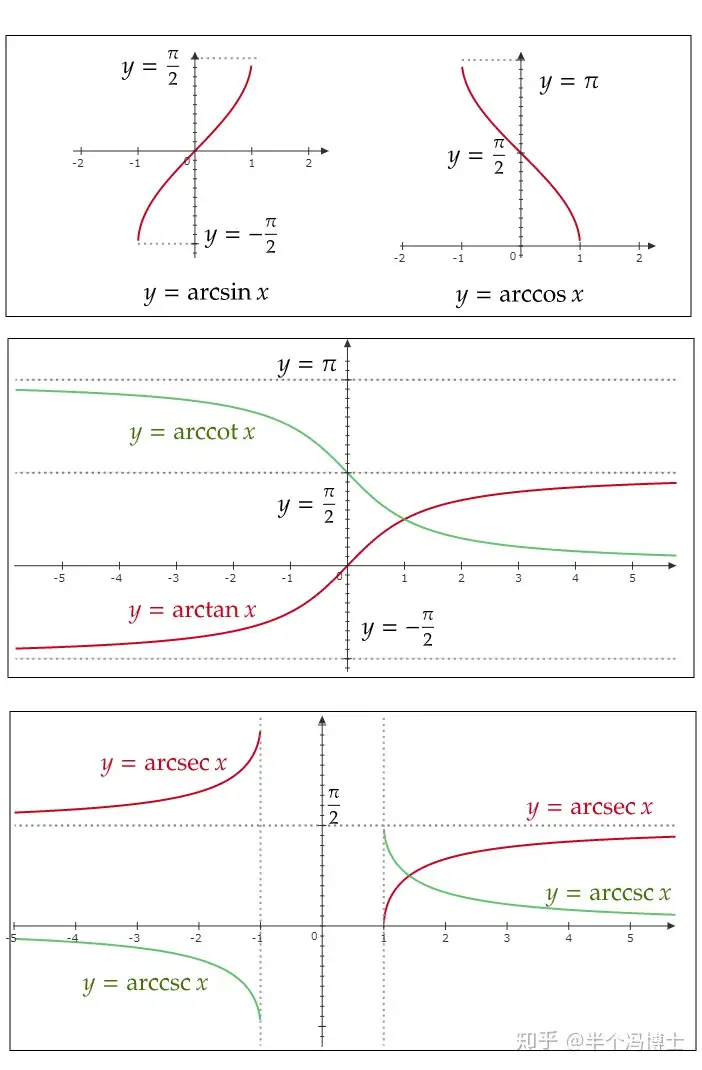
图3.反三角函数的图象
在使用反三角函数时一定要注意其定义值和值域。
表1. 反三角函数的定义值及值域 反三角函数
三角函数定义域值域
二、反三角函数的导数的推导过程
反函数求导公式在另一篇笔记里已经回顾过:关于反函数的高阶导数
反函数的导
数等于直接函数的导数的倒数。
先给结论:
表2. 反三角函数的导数及其定义域
编号
导数定义域
接下来依次证明:
1、反正弦函数
的导数
2、反余弦函数
的导数
证法I: 类似推导
证法II:由
,于是
3、反正切函数
的导数
4、反余切函数
的导数
证法I:类似3,略。
证法II: 类似2,由
,于是
5、反正割函数
的导数
标部分主要是要把上一步完全由 表示,由于有以下恒等关系
i)
因此:
ii) 这时必须注意到 的取值范围 (见表1.)。而在这一步中不能取任何一个端点。同时注意到:
时: 都大等于
时: 都小等于
因此:
综上:标
步的写法可以保证这一不等关系始终成立。
6、反余割函数
的导数
证法I:类似5,略。
证法II: 类似2,由
,于是
小结
本文简单总结了反三角函数的定义、其对应的三角函数、其定义域、值域,其后利用反函数求导法则完成了所有反函数求导公式的推导证明。不难看出上述推导过程其实都并不复杂(除反正割、反余割函数外),若能熟练使用各种三角函数变换技巧则能轻松完成所有证明。在实际使用三角函数时,图1,图2给出的图示十分有用,尤其在考虑积分换元时。另外,在使用反三角函数时,一定要明确各个三角函数的定义域及值域,这一点在第5个证明中体现得较为明显。若忽视这些细节,则十分容易出错。
引用https://zhuanlan.zhihu.com/p/201720785
标签:三角函数,导数,值域,及其,证法,定义域,反函数 From: https://www.cnblogs.com/shiyh/p/17384702.html