\(1.\)
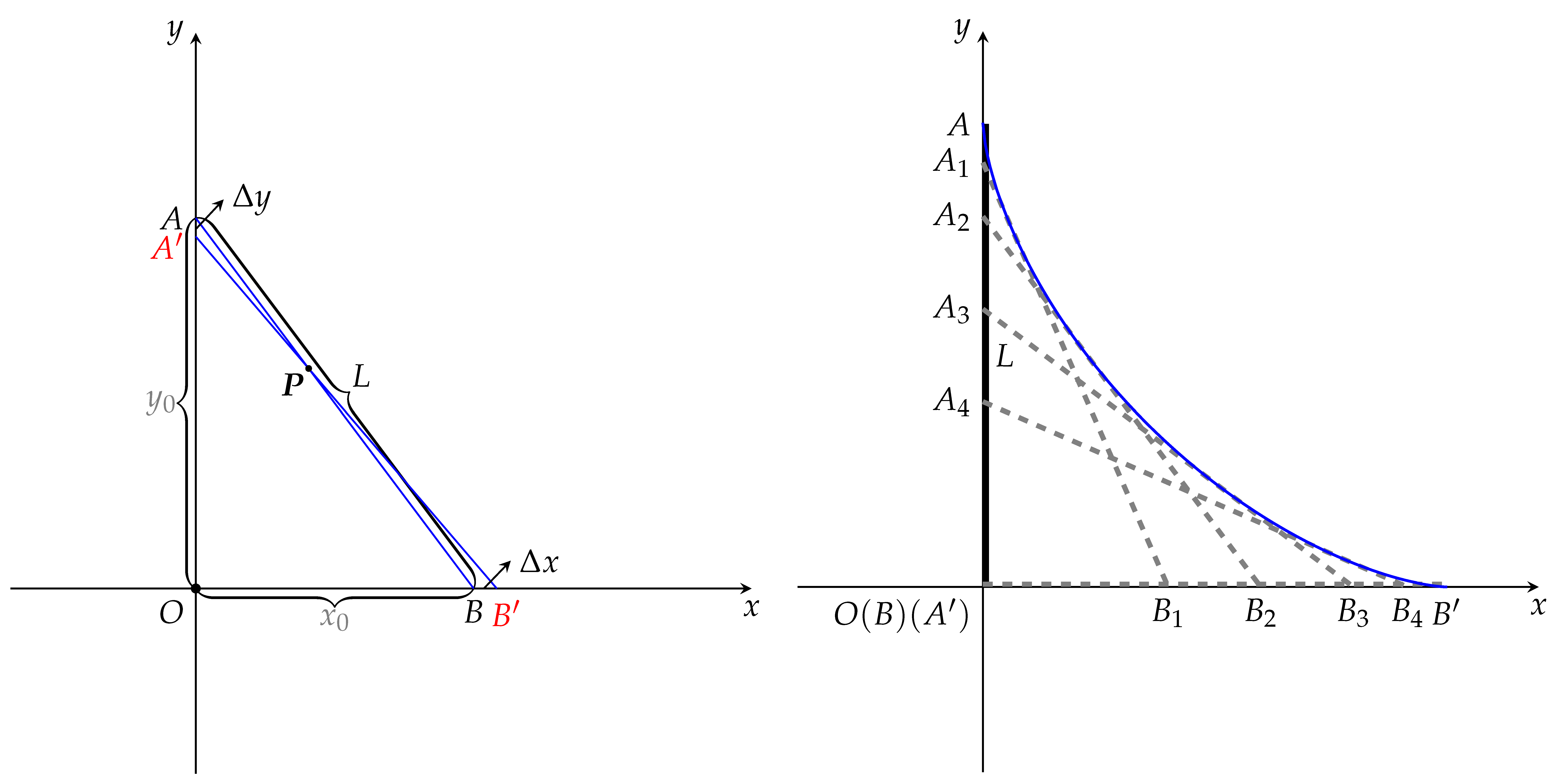
如图所示,一硬杆 \(AB\) 竖立靠在墙角,受外力作用下滑,顶部与底部始终接触墙面和地面,直至完全倒下.
若杆长为 \(L\) ,粗细不计,求杆扫过的图形的面积以及围成此图形的一段曲线的函数解析式.
\(\large \cal My \ Solve:\)
设在杆下滑时的某一时刻,杆上端 \(A\) 位于 \((0, y_o)\),下端 \(B\) 位于 \((x_0, 0)\) \((0 \le x_0 \le L \:, 0 \le y_o \le L)\).
则有: \(x_0 ^2 + y_0^2 = L^2\).
再设经过极小时间后,\(A\) 下移了 \(\Delta y\) 至 \(A'(0, y_0 - \Delta y)\),\(B\) 右移了 \(\Delta x\) 至 \(B'(x_0 + \Delta x, 0)\).
此时仍有 :\((x_0 + \Delta x)^2 + (y_o - \Delta y)^2 = L^2\).
两市结合得:
\(x_0 ^2 + y_0^2 = (x_0 + \Delta x)^2 + (y_o - \Delta y)^2\)
则 \(\Delta y = \cfrac{x_0}{y_0} \Delta x\) (此处忽略了高阶无穷小)
此时用待定系数法解出 \(AB\),\(A'B'\) 解析式.
易得:
\(AB : y = -\cfrac{y_0}{x_0}x + y_0\).
\(A'B' : y = -\cfrac{y_0 - \Delta y}{x_0 + \Delta x}x + y_0 - \Delta y\).
将 \(\Delta y\) 用 \(\Delta x\) 表示,并联立求出交点 \(P\) 的横坐标的表达式:
\(\begin{cases} y = -\dfrac{y_0}{x_0}x + y_0 \\ y = -\dfrac{y_0 - \cfrac{x_0}{y_0} \Delta x}{x_0 + \Delta x}x + y_0 - \cfrac{x_0}{y_0} \Delta x \end{cases}\)
解得:\({\large x}_P = \dfrac{x_0^3}{x_0^2 + y_0^2}\)(此处有一个 \(\Delta x\) 化不掉我就直接忽略了).
即:\({\large x}_P = \dfrac{x_0^3}{L^2}\).
由对称性可知 \({\large y}_P = \dfrac{y_0^3}{L^2}\).
而由于 \(\Delta x \to 0\) ,那么 \(P\) 就在所求曲线上.
于是可以得到所求曲线的参数表达式:
\(\begin{cases} x = \dfrac{x_0^3}{L^2} \\[1ex] y = \dfrac{y_0^3}{L^2} \\[1ex] x_0^2 + y_0^2 = L^2 \end{cases}\)
解析式也就容易求出来了:\(y = \left(L^{\tfrac 23} - x^{\tfrac 23}\right)^{\tfrac 32} (0 \le x_0 \le L)\)
所求图形面积直接用解析式积分不好求,故利用参数方程,并设 \(AB\) 与 \(y\) 轴夹角为 \(\theta\).
则:\(\begin{cases} x_0 = L \sin\theta \\ y_0 = L \cos\theta \end{cases}\)
曲线参数方程可化为:
\(\begin{cases} x = L\sin^3\theta \\[1ex] y = L\cos^3\theta \end{cases}\)
上式两边同时微分得:
\({\rm d}x = 3L\sin^2\theta\cos\theta \ {\rm d}\theta\).
故:
\(\begin{aligned} S & = \displaystyle\int_0^L y \ {\rm d}x \\[1ex] & = \int_0^{\tfrac \pi2} L\cos^3\theta \cdot 3L\sin^2\theta\cos\theta \ {\rm d}\theta\\[1ex] & = 3L^2 \int_0^{\tfrac \pi2} \cos^4\theta \sin^2\theta \ {\rm d}\theta\\[1ex] & = 3L^2 \left[\dfrac 1{48} \sin^3 2\theta - \dfrac 1{64} \sin 4\theta + \dfrac 1{16} \theta \right]_0^{\tfrac \pi2} \\[1ex] & = \dfrac{3\pi}{32} L^2 \end{aligned}\)
标签:题目,dfrac,Delta,1ex,sin,theta,一些,有趣,cases From: https://www.cnblogs.com/ZZM-248/p/17365916.html