深度学习的实践层面
训练集 验证集 测试集
过程
神经网络的训练是一个需要不断迭代的过程,一般先提出idea,然后编码实现、测试,根据测试结果再次调整思路......
分组与比例
数据集通常分为3个部分:训练集、验证集和测试集。
- 训练集用于训练模型的参数。
- 验证集用于选择最好的模型。
- 测试集用于评估训练结果。
一般讲数据集按照60%训练,20%验证和20%测试集来划分。
当数据集的大小达到一百万时,则比例可以调整为98%+1%+1%,因为验证集和测试集实际上不需要太多。
如果超过百万级别,甚至可以调整为99.5%+0.25%+0.25%.
分布
训练集、验证集和测试集应当保证分布一致。
防止出现这种情况:在分辨猫图片的模型训练中,如果训练集都是猫的图片,本来训练得很好,但是测试集都是狗的图片,结果得到了很差的评估。
偏差 方差
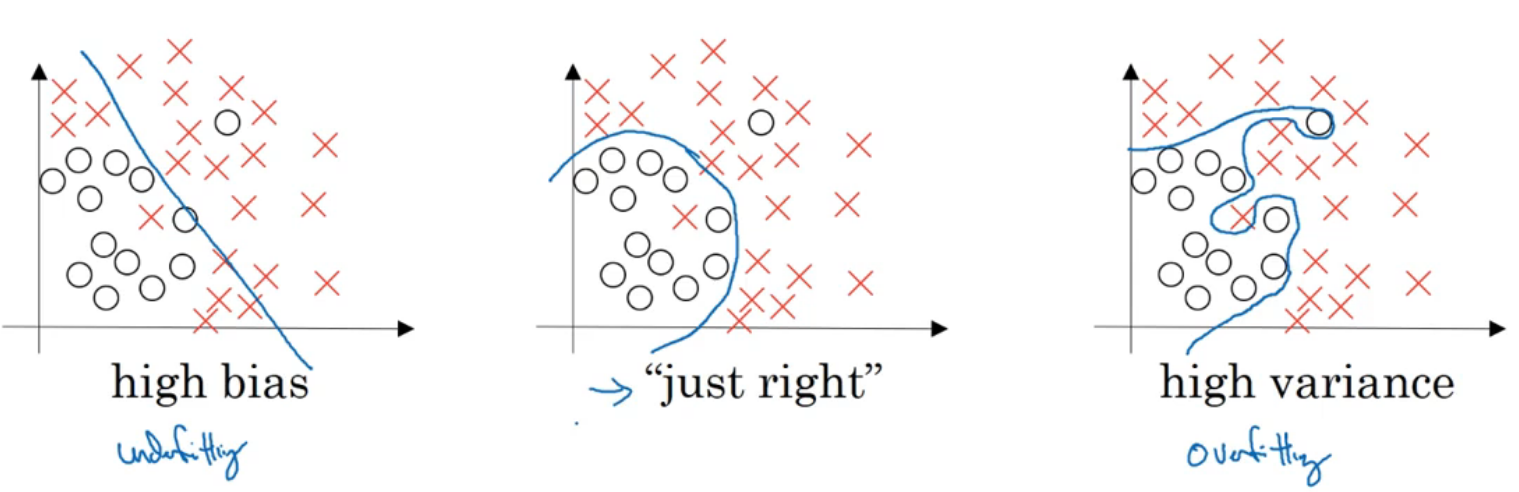
- 高偏差:欠拟合
- 高方差:过拟合
如果出现高偏差问题,一般无法通过增加数据量解决问题。如果出现高方差问题,可以尝试使用正则化。
正则化
一般使用正则化来防止出现过拟合现象。
使用正则化会引入超参数\(\lambda\)。
可以只正则化参数\(W\),因为偏置项\(b\)只是单个数字,正则化的意义不大。
L2正则化
正则项为:
\[\frac{\lambda}{2m}\parallel w \parallel_2^2=\frac{\lambda}{2m}\sum\limits_{j=1}^{n_x}w_j^2 \]其中\(\parallel w\parallel_2\)为\(w\)的L2范数,也叫欧几里得范数。
L1正则化
使用的是L1范数,会使得模型变得稀疏(部分参数变为0)。
L2正则化是较为常用的。
正则化如何生效?
误差函数\(J\)中加入了正则项,而\(J\)的值又会影响参数的更新。
如果\(\lambda\)太大了,就会导致\(W\)几乎为0,使得模型变得简单,甚至可能欠拟合。
如果\(\lambda\)太小,对\(W\)的修正效果不大,如果原先模型就有过拟合现象,则不能很好的解决问题。
dropout正则化
随机失活,到达某一层的时候,会先遍历该层结点,以一定的概率(超参数)决定是否将其失活。
通过随机失活可以避免一些\(W\)变得太大,导致过拟合。
使用dropout正则化之前,\(a\)的原本值假设是100,使用dropout正则化之后,如果存活概率设置为80%,那么\(a\)的值可能变为80,为了保持数值,应该计算a=a/0.8。
实施dropout正则化的相关知识:
- 每层的存活率可以设置不同值,做出相应调整,但是会引入较多超参数。
- 通常存活率不能设置太低,最好接近1,甚至大多数时候是不需要失活的,某些层直接设置为1。
其它正则化方法
-
数据扩增
如果数据集是图像,可以考虑通过旋转,翻转等操作来扩增数据集。
-
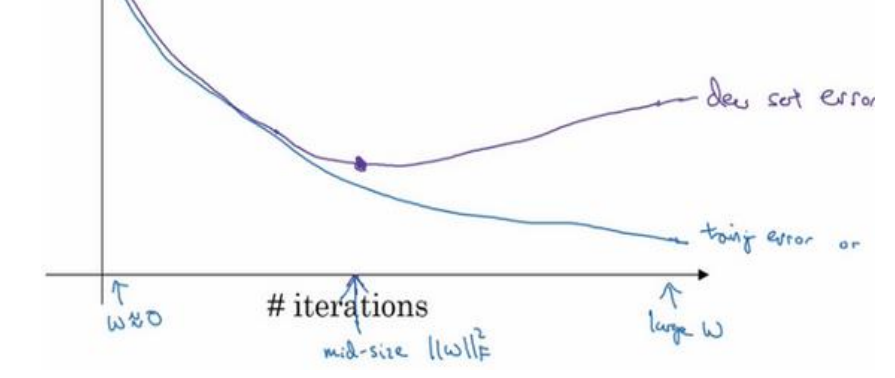
early stopping
有时候迭代次数太多反而得到较差的结果,提前结束训练可以得到较好结果。
归一化
可以使数据分布得更”均匀“
思路和标准化正态分布是一致的:
- 求均值。
- 求方差。
- \(X:=\frac{X-\mu}{\sigma^2}\)
归一化可以提高训练速度。
梯度爆炸和梯度消失
这个问题通常发生在层数较多的神经网络。
梯度爆炸:如果每个权重\(W\)都大于1,那么不断地乘上\(W\),到最后输出值会变得非常大。
这种情况下,可能导致\(W\)的值越来越大,最后甚至溢出为NaN.
梯度消失:如果每个权重\(W\)都小于1,那么不断地乘上\(W\),到最后输出值会变得非常小。
这种情况下,可能因为梯度太小,导致梯度下降速度缓慢。
权重初始化
合理的权重初始化可以缓解梯度爆炸和梯度消失带来的痛点。
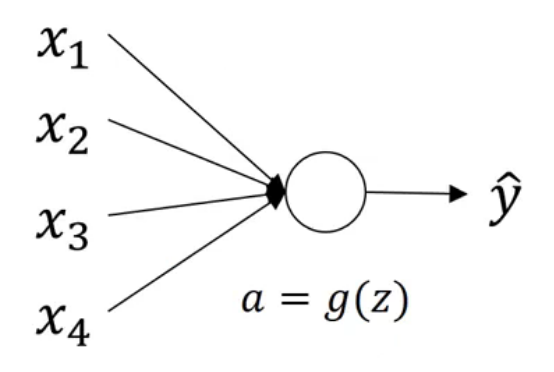
对于上图这种简单案例,有:
\[z = \sum\limits_{i=1}^nw_ix_i \]可以考虑将权重初始化为:
\[w_i=\frac{1}{n} \]其它激活函数
-
如果使用的是Relu,则建议\(w_i=\frac{2}{n}\)
-
如果使用的是\(\tanh\),则建议\(w_i=\sqrt{\frac{1}{n}}\)
梯度的数值逼近
联系导数与导数的近似值即可:
-
\(f'(x)=\lim\limits_{\epsilon\to0}\frac{f(x+\epsilon)-f(x-\epsilon)}{2\epsilon}\)
-
\(f'(x)\approx\frac{f(x+\epsilon)-f(x-\epsilon)}{2\epsilon}\)
梯度检验
- 将\(W\)和\(b\)都扁平化组合起来,形成一个向量\(\theta\)
- 将\(dW\)和\(db\)都扁平化组合起来,形成一个向量\(d\theta\)
则误差函数\(J(W,b)\)可以记为\(J(\theta)\).
对于向量\(\theta\)的每一项\(\theta_i\),我们可以计算其近似值:
\[d\theta_{approx}[i]=\frac{J(\theta_1,\theta_2,\cdots,\theta_i+\epsilon,\cdots)-J(\theta_1,\theta_2,\cdots,\theta_i-\epsilon,\cdots)}{2\epsilon} \]这个近似值应该接近它的真实值:\(d\theta[i]\)
评估指标
\[\frac{\parallel d\theta_{approx}-d\theta\parallel_2}{ \parallel d\theta_{approx}\parallel_2 +\parallel d\theta\parallel_2 } \]分子部分:欧几里得范数,计算两个向量”终点“之间的”距离“。
分母部分:防止分子数值相差过大,分母将这个指标变成一种”比率“。
参考数值
- 如果指标的数量级为\(10^{-7}\),则是好的结果。
- 如果指标的数量级为\(10^{-5}\),中规中矩,可能有问题。
- 如果指标的数量级为\(10^{-3}\),则是坏的结果,需要调整。
注意事项
- 不要在训练中使用梯度检验,只用于调试。
- 如果算法的梯度检验失败,要检查所有项,检查每一项,并试着找出 bug。
- 梯度检验不能与dropout同时使用,因为每次迭代过程中,dropout会随机消除隐藏层单元的不同子集,难以计算dropout在梯度下降上的代价函数\(J\)
标签:DL,frac,层面,ML,epsilon,正则,梯度,theta,parallel From: https://www.cnblogs.com/feixianxing/p/deep-learning-practice.html