山东省集 2023.4.24 HeRen 场 T2

简要题意

数轴上有 \(n\) 个点，给定其坐标 \(x_i\)。给定 \(d\)，你可以将任意多个点的坐标增加 \(2d\)。给定 \(a, b\)，接下来你可以放置若干个区间在数轴上，设某个区间 \([l, r]\)，其代价是 \(a + b(r - l)\)。所有点都要被你放置的区间覆盖，求最小代价。

数据范围：\(1\le n, d, x_i \le 150, 1\le a, b \le 10^6\)。

题解

可以将移动点这个限制转化为 \(x_i\) 和 \(x_i + d\) 中至少有一个被覆盖。一开始令 \(b \leftarrow \min(a, b)\)，设 \(p_i\in\{0, 1\}\) 表示一个点有没有被覆盖，那么对于一个位置 \(i\) 如果 \(p_i = 0, p_{i+1} = 1\) 那么代价为 \(a\)，如果 \(p_i = p_{i+1} = 1\) 那么代价为 \(b\)。

注意到计算贡献和考虑合法性时，一个位置 \(x\) 需要去感知的位置是 \(x - 1, x + 1, x - 2d, x + 2d\)。这启发我们把转移排列成一个 \(\frac{X}{2d}\times2d\) 的方阵，然后在上面转移。那么注意到 \(X \le 450\)，则长和宽中至少有一个不超过 \(21\)。进行类似插头 \(\text{DP}\) 的操作即可。

如果这题的移动不是 \(2d\) 而是 \(2d + 1\) 的话，据说存在一种简单的网络流解法。我还没有想出来，\(\text{HeRen}\) 没讲，去问 \(\text{ybw051114}\)，他也不想深入考虑。这里先贴一个结构。

当距离是奇数的时候，形如“两个位置中至少选择一个”的限制构成了一张二分图，这时候有一种最小割结构可以实现限制：

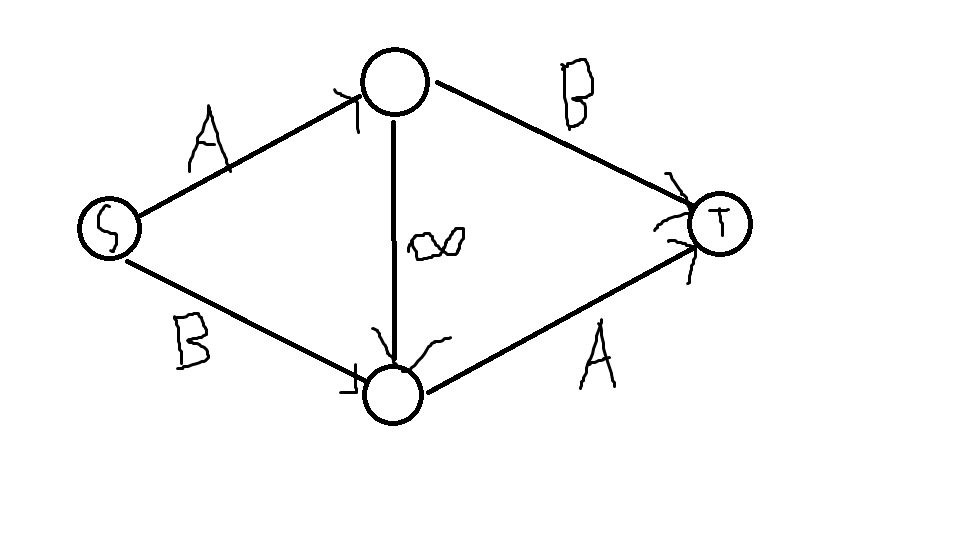
其中，对于 \(A\) 类边如果割掉，表述的是选择这个对象，\(B\) 类表述不选择，二分图左部点把 \(A\) 类边放在源点方向，而右部点放在汇点方向，中间的边使得我们不能两个都割掉 \(B\)，也就是我们不能两个都不选。这个图同样可以扩展为至多选一个以及刚好选一个。

后面我就不会了。