胡测 7
我怎么这么菜!我怎么这么菜!我怎么这么菜!
T1 命题
从内到外考虑,设 \(f(i,s1,s2)\) 为当前位置 \(i\) ,\([i+1,n]\) 部分 \(x\) 取值为 \(s2\),\([1,i]\) 部分每个位置上是全称量词或存在量词取值为 \(s1\) 的情况下命题是否成立,这样 DP 时从 \(i-1\) 到 \(i\) 的转移就是第 \(i\) 的状态由表示取值到表示量词,分别用与运算和或运算转移到全称和存在即可。
复杂度 \(O(n2^n)\)。
本题关键是设计状态,赛时一直在考虑如何把取值集合通过卷积之类的操作过渡到量词集合,这样似乎是复杂而困难的。
T2 分组
钦定 \(B\) 先放满,方案数在此基础上乘 \(2\)。
枚举放满 \(B\) 的最后位置,容易发现这个位置一定不能是 \(2n\),否则 \(A\) 先放满。在 \(B\) 放满后,后面的人都会被分到 \(A\) 中,因此如果后面有被询问的人,询问集合整体都分到 \(A\) 中,反之则分到两组均可。
由于不同的最后位置的方案数与前缀有多少被询问的人有关,所以考虑枚举被询问的人的个数。写出式子:
\[2\times \dfrac{1}{2^n}\left(\sum_{i=0}^k \sum_{j=p_i+1}^{p_{i+1}-1}2^{2n-j}\dbinom{j-i-1}{n-1}+2^{2n-p_k}\dbinom{p_k-k}{n-k}[p_k<2n]+\sum_{j=p_k+1}^{2n-1} 2^{2n-j}\dbinom{j-k-1}{n-k-1}\right) \]第一部分是分到 \(A\) 组的方案,实际上就是 \(j\) 后面的位置无关紧要(\(B\) 已经填满,任何结果都会分到 \(A\) 组),前面的结果除了最后一个位置 \(j\) 一定是 \(B\),被询问的位置一定是 \(A\),其余位置中再选出 \(n-1\) 个组成 \(B\)。同时根据当前统计的情况,被询问的位置一定不是最后一个填 \(B\) 的位置。
后面两部分本质相同,是分到 \(B\) 组的方案,与上面的唯一区别是除了最后一个和被询问的以外,其余位置中选出 \(n-k-1\) 个 \(B\)。但比较特殊的是恰好 \(p_k\) 在位置放满,此时有 \(k\) 个位置被钦定而不是 \(k+1\) 个。
考虑化简式子。
把前半部分拿出来处理一下:
\[\begin{aligned} &\sum_{i=0}^k \sum_{j=p_i+1}^{p_{i+1}-1}\dfrac{1}{2^j}\dbinom{j-i-1}{n-1}\\ =&\sum_{i=0}^k \sum_{j=p_i+1}^{p_{i+1}-1}\dfrac{2^{-i}}{2^{j-i}}\dbinom{j-i-1}{n-1}\\ \end{aligned}\]设 \(f(x)=\dfrac{1}{2^x}\dbinom{x-1}{n-1}\),则化简成:
\[\begin{aligned} &\sum_{i=0}^k \dfrac{1}{2^i}\sum_{j=p_i+1-i}^{p_{i+1}-1-i} f(j)\\ \end{aligned}\]这部分可以前缀和 \(O(k)\) 求了。
后半部分实际上是只关于 \(k\) 的前缀和,而由于 \(\sum k\) 与 \(n\) 同级,所以 \(k\) 取值只有 \(O(\sqrt{n})\) 种,可以预处理。
总复杂度 \(O(n\sqrt{n})\)。
T3 题目
LIS 容易想到偏序关系,容易想到建有向图。
最朴素的建图是满足 \(i<j,a_i+1=a_j\) 的连 \(j\to i\),满足 \(i<j,a_i=a_j\) 的连 \(i\to j\)。
结合样例 \(a=\{1,2,3,3,3,3,2,1,4,1\}\),发现 \(p_6<p_9\) 是必须成立的。
证明:假设 \(p_6>p_9\),则为了保证 \(a_9=4\),一定存在 \(i\) 满足 \(i<9,a_i=3\) 且 \(p_i<p_9\),此时 \(a_i=a_6=3\) 所以 \(p_6<p_i<p_9\),假设不成立。
在此基础上有 \(p_6<p_5<p_4<p_3\),所以 \(p_3,p_4,p_5\) 的取值已然和 \(p_9\) 无关了,也就是一个位置 \(j\) 之和它前面第一个满足 \(a_i+1=a_j\) 的 \(i\) 有限制关系,也就是只连一条边。
现在只要求出能到达一个节点的节点个数,就是其在最好情况下从大到小的排名。为了减少边数,\(a\) 相同的边只连相邻的一条,边数达到 \(2n\)。
直接拓扑排序会算重,结合一张图理解一下:
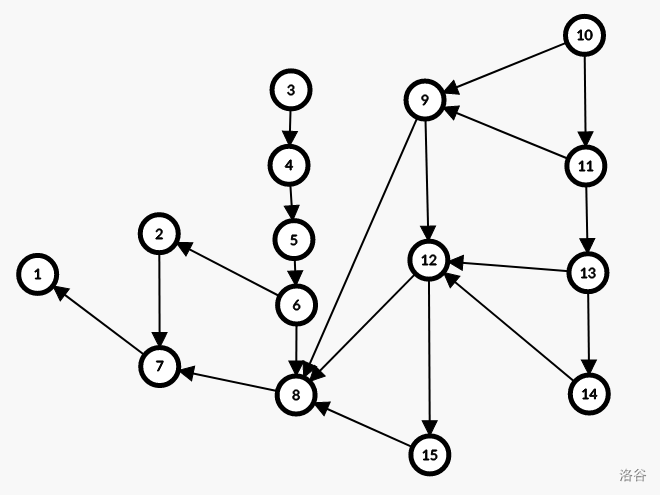
这是按照上面要求建好的图,容易发现 \(9\) 分别直接或是通过 \(12\) 或 \(15\) 对 \(8\) 产生贡献,会重复,而 \(10,12,13\) 也是同样的情况,不如删去这些边,不会影响答案。所以对于一个起点,只连终点最大的一条,在此基础上,对于一个终点,只连起点最大的一条。
如下图:
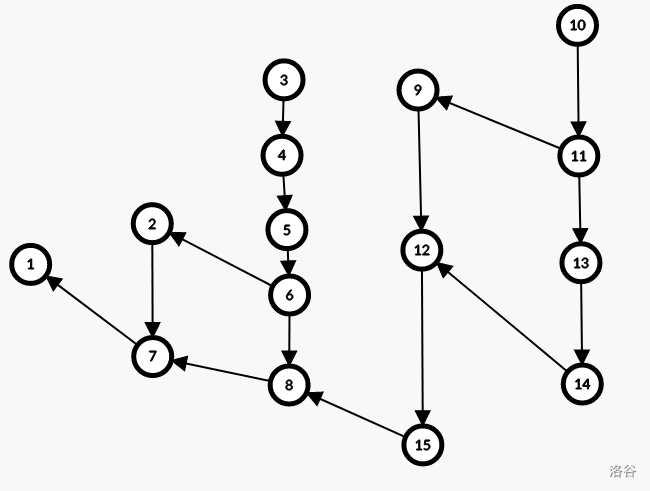
这样每个节点的入边最多只有两条:同层和跨层各一条。
对于 \(7\) 这种情况,从两条边都转移会有重复,重复部分实际上在 \(7\) 上面层当中,而 \(8\) 恰好统计了这些层中全部答案(结合同层边以及连边只连起点最大的一条不难理解),剩余的节点就是与 \(7\) 同层且更靠前的节点,所以可以只从 \(8\) 转移,再加上同层更靠前的节点数。
对于只有一条边的节点,直接转移即可。
标签:考后,dfrac,sum,位置,清北营,放满,节点,模拟,dbinom From: https://www.cnblogs.com/SoyTony/p/Problems_in_April_THUSC_and_PKUSC_Simulations_2.html