第一节简述人类视觉系统的一些重要方面,包括人眼中图像的生成及人眼适应和辨认灰度的一些能力,第二节讨论光、电磁波谱的其他分量及他们的成像特点,第三节讨论成像传感器及如何使用成像传感器来生成数字图像,第四节介绍均匀图像取样和灰度量化的概念,第五节介绍像素间的各种基本关系
视觉感知要素
目的:图像形成并被人类感知的基本原理
- 光感受器:锥状体(对颜色高度敏感,明视觉或亮视觉),杆状体(对低光照度敏感,表现为白天色彩鲜艳的物体在月光下却没有颜色,因为此时只有杆状体受到刺激,暗视觉、微光视觉)
- 人眼通过调节晶状体的形状来调节焦距,物体在视网膜上成像,光感受器的相对激励作用产生感知,把辐射能量转换为最终由大脑解码的电脉冲
- 感知亮度不是实际灰度的简单函数,视觉系统往往会在不同灰度区域的边界处出现下冲和上冲的现象,马赫带效应;同时对比,在背景不同的时候,人眼会对实际灰度相同的物体感到不同的亮度;光觉错视表示一些视觉上面的错觉;
光和电磁波谱
- 电磁波谱可用波长、频率或能量表示,波长\(\lambda\)和频率\(v\)的关系为:
\(c\)是光速\(2.998 \times 10^8m/s\)
电磁波谱各分量的能量为:
\(h\)是普朗克常数,能量和频率成正比,和波长成反比
- 可见光的范围为\(0.43\mu m\)紫色~\(0.79\mu m\)红色
- 感知的物体颜色由物体反射的光的性质来决定
- 没有颜色的光称为单色光或无色光,单色光的唯一属性是亮度,单色光的感知亮度是从黑色到灰色最后到白色变化,单色光从黑到白的数值范围通常称为灰度级,单色图像称为灰度图像
- 辐射:从光源流出的总能量,用瓦特来度量
- 光通量:观察者从光源感知的能量,用流明\(lm\)来度量,例如不可见光的流明几乎为0
图像感知与获取
- 由“照射”源和形成图像的“场景”元素对光能的反射或吸收产生的,传感器对正被检测能量类型的响应,将入射能量转换为电压,输出电压波形是传感器的响应,将传感器响应数字化,得到一个数字量
- 光二极管:输出是与光强成正比的电压
- 一个简单的成像模型:以\(f(x,y)\)的二维函数来表示图像,\(i(x,y)\)表示入射分量,表示入射到被观察场景的光源照射量;\(r(x,y)\)表示反射分量,限制在0(全吸收)和1(全反射)之间:
图像取值和量化
目的:将连续观测的数据(例如电压)转换为数字形式,这种转换包括取样和量化
- 对坐标值进行数字化称为取样或采样,对幅值进行数字化称为量化,也就是对一幅连续的图像划分为一个个小格子以对坐标值量化,后对每一个格子取值以对灰度值量化;
- \((x,y)\)是笛卡尔积\(Z^2\)中的整数,且\(f\)是把灰度值(即实数集\(R\)中的一个实数)赋给每个特定坐标对\((x,y)\)的一个函数,那么\(f(x,y)\)就是一幅数字图像;
- 灰度级\(L\)出于对存储和量化硬件的考虑通常取\(2\)的整数次幂;
- 灰度跨越的值域称为动态范围,定义为最大可度量灰度与最小可度量灰度之比;
- 图像对比度定义为一幅图像中最高和最低灰度级间的灰度差
- 一个像素的位置有坐标索引或下表索引\((x,y)\),和线性索引,线性索引分为行扫描和列扫描,以列扫描为例,从最左边一列开始,从上到下从0开始标号,之后到第二列,接着第一列最后一个号标号,后面的列以此类推;
- 空间分辨率:单位距离的线对数和单位距离的点数(像素数)单位(dpi,点数/英寸)
- 灰度分辨率:量化灰度时的比特数,例如灰度被量化为256级的图像,其灰度分辨率为8比特
- 图像内插:通常在图像放大、缩小、旋转和几何校正等任务中使用,主要是用已知数据估计未知位置的值的过程,包含最近邻内插、双线性内插,双三次内插
像素间的一些基本关系
- 坐标\((x,y)\)处的像素\(p\)有两个水平的相邻像素和2个垂直的相邻像素,坐标分别是\((x + 1,y),(x - 1,y)(x,y+1),(x,y-1)\),这组像素称为\(p\)的4邻域,用\(N_4(p)\);
- \(p\)的4个对角邻域的坐标是\((x+1,y+1),(x+1,y-1),(x-1,y+1),(x-1,y-1)\),用\(N_D(p)\)表示;
- \(p\)的4个对角邻域和4邻域合起来合称\(p\)的\(8\)邻域,用\(N_8(p)\)表示;
- 如果一个邻域包含\(p\),称为闭邻域,否则称为开邻域;
- 对于坐标分别为\((x,y),(s,t),(v,w)\)的像素\(p,q,z\),如果:
则称\(D\)是距离函数或度量
- 欧氏距离:\(D_e(p,q) = [(x - s)^2 + (y - t)^2]^{\frac{1}{2}}\)
- \(D_4\)城市街区距离:\(D_4(p,q) = |x - s| + |y - t|\)
- \(D_8\)棋盘距离:\(D_8(p,q) = max(|x - s|,|y - t|)\)
涉及数学工具
- 图像的阵列操作:逐像素操作
- 考虑一般的算子\(H\),该算子对于给定的输入图像\(f(x,y)\),产生一幅输出图像\(g(x,y)\):
如果:
\[H[a_if_i(x,y) + a_jf_j(x,y)] = a_iH[f_i(x,y)] + a_jH[f_j(x,y)] = a_ig_i(x,y) + a_jg_j(x,y) \]则称\(H\)是一个线性算子,符合加性和同质性或齐次性
- 图像相加:去噪,现有照片是原图像加上加性噪声形成的,噪声的平均值为0,所以多张带噪声的图片相加平均可以起到去噪的效果
- 图像相减:增强图像之间的差,可以看清血管,用使用造影剂前后的图像相减即可得到血管
- 图像相乘:阴影校正,假设现有图像是由原图像乘上一个阴影函数,那么我们利用阴影函数的反函数就可以得到原图片,修正光线的影响;
- 单像素操作:通过变换函数改变某像素点的灰度值
- 领域操作:变换后的图像里面的某一点的像素值由以该点为中心的邻域内所有点计算而来;
- 几何变换:包含坐标的空间变换和灰度内插两个过程
坐标转换:仿射变换,假设\((x,y)\)是变换后的坐标,\((v,w)\)是变换前的坐标,下面的公式是前向映射,也就是将变换前的坐标转换到变换后的坐标
还可以做反向映射,也就是由转换后的图像的坐标计算出变换前所在的原图中的坐标,这种方法更加有效:
\[[ \begin{matrix} v & w & 1 \end{matrix} ] = T^{-1}[ \begin{matrix} x & y & 1 \end{matrix} ] \]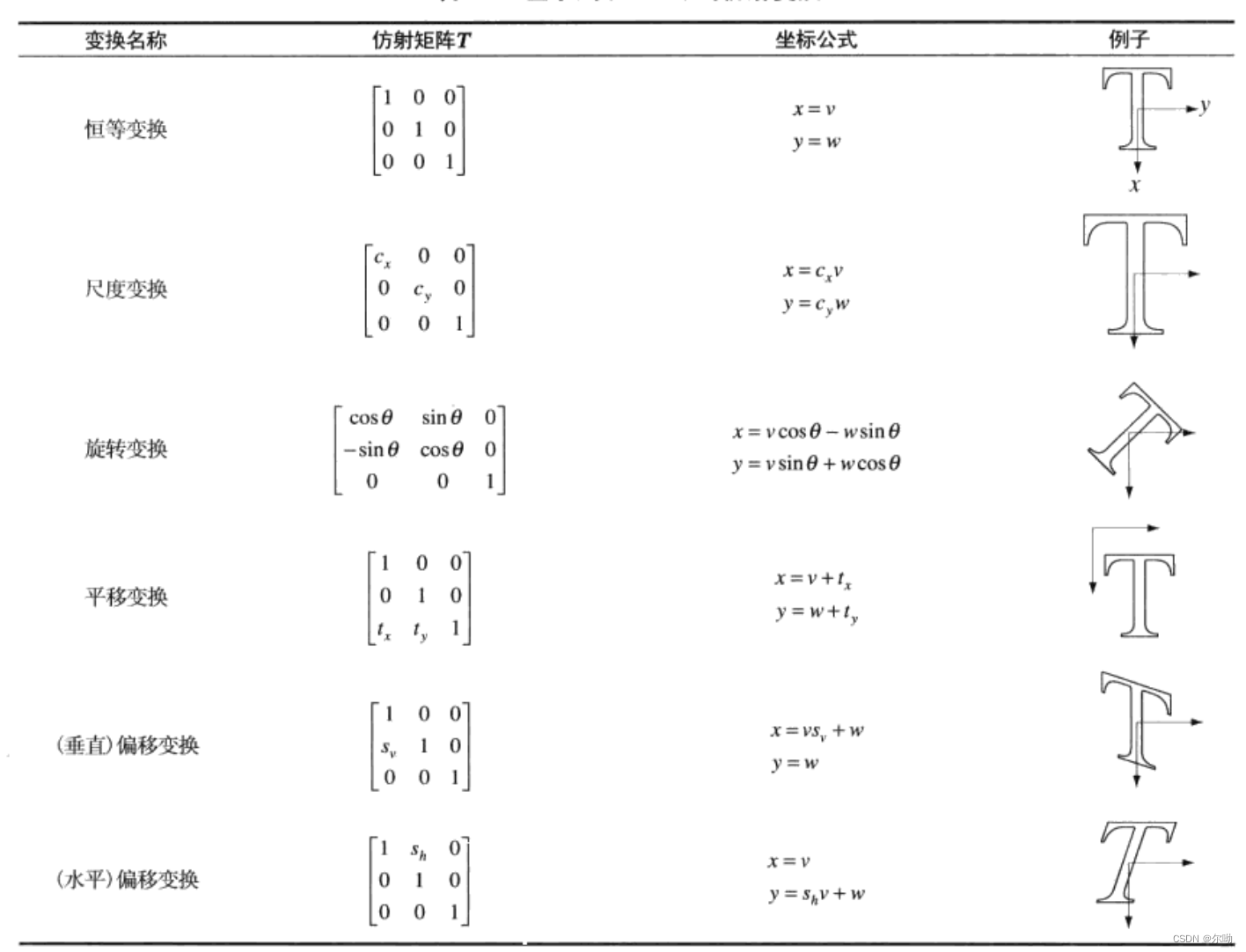
灰度内插:最近邻、双线性、双三次内插
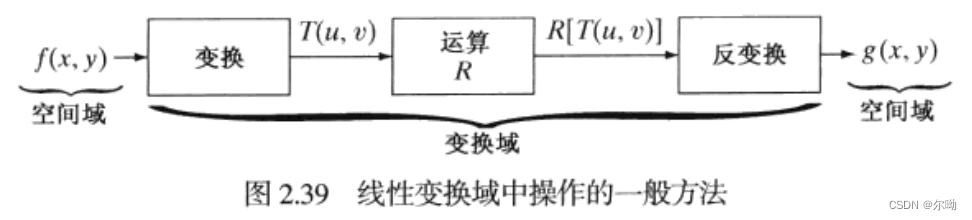
- 图像变换:之前介绍的任务是直接在空间域工作,在一些情况下,可以变换图像,然后在变换域执行指定的任务,之后再反变化到空间域,二维线性变换\(T(v,u)\):
其中,\(f(x,y)\)是输入图像,\(r(x,y,u,v)\)是正变换核,上式对\(u = 0,1,2,\cdots,M-1,v = 0,1,2,\cdots,N-1\)计算,\(x,y\)是空间变量,\(M,N\)是\(f\)的行和列,\(u,v\)是变换变量,\(T(u,v)\)称为\(f(x,y)\)的正变换,还可以用\(T(u,v)\)反变换\(f(x,y)\):
\[f(x,y) = \sum_{u = 0}^{M - 1}\sum_{v = 0}^{N - 1}T(u,v)s(x,y,u,v) \]\(s(x,y,u,v)\)称为反变换核