P3205 [HNOI2010]合唱队
区间DP——取一端
思:
根据题意我们发现,每次排队的时候,会出现两种情况
- 当前排入的人(即初始队列最后一人)比初始队列中前一个人矮,排到最左边
- 当前排入的人(同上)比初始队列中前一个人高,排到最右边
可从初始队列最后一人切入。
设置状态:\(f[l][r][0/1]\)表示初始队列最后一个人排到理想队列\(l\)~\(r\)的队首或队尾,f存的值为原始队列的方案数。
0表示从插入队头,1表示插入队尾。
原始推目标,目标再推回原始。感觉有点绕,画图大法非常好。
(以最后一人插入队头为例,插入队尾举一反三.
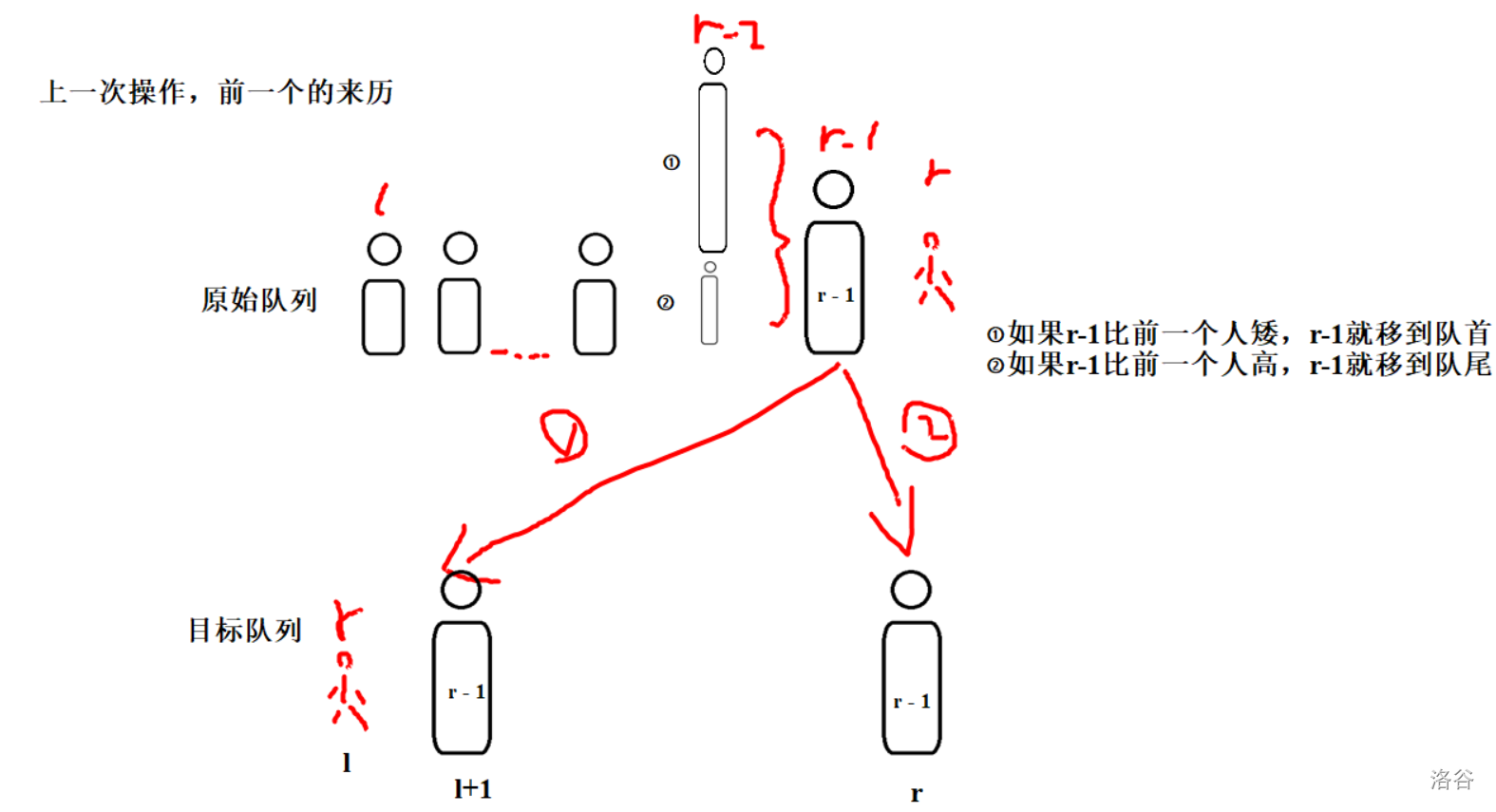
通过\(h[l]\)与\(h[l+1]\)和\(h[r]\)的关系来判断最后一人r与前一人r-1的关系。
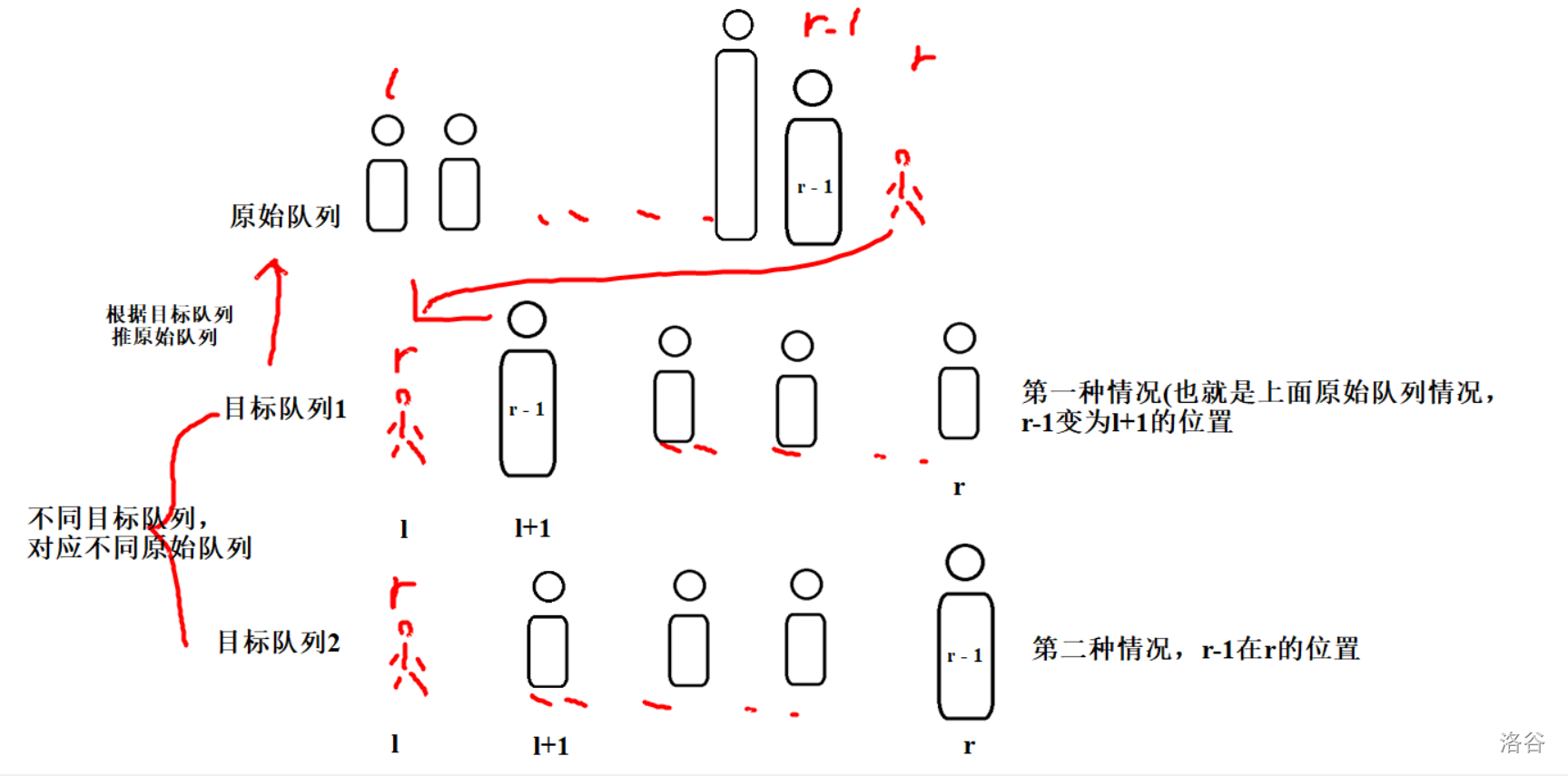
举样例:
4
1701 1702 1703 1704
枚举区间1~3(1701,1702,1703)时
1701的前面若是1702(a[l]<a[l+1]),则原始序列中1702是比前一个人矮才来到2~3的队首。
1701的前面若是1703(a[l]<a[r]),则原始序列1703是比前一个人高才来到2~3的队尾。
(防止混淆,不是1702既来队首,又有来队尾的可能。
注意初始化。
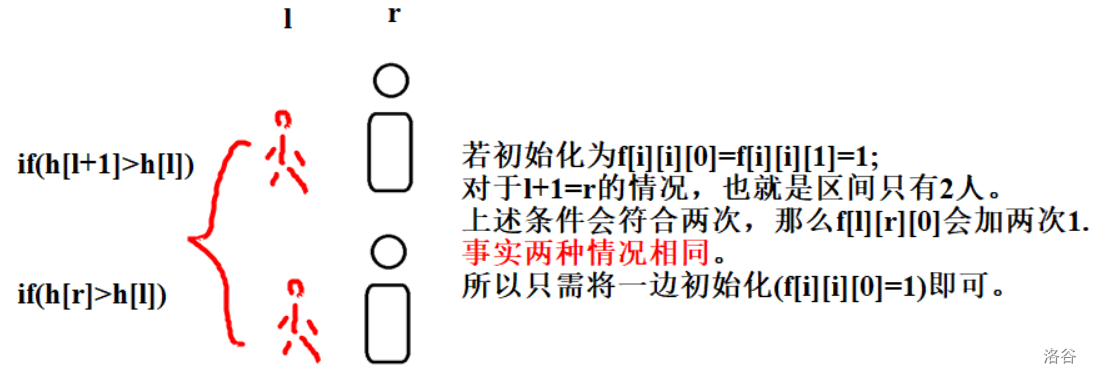
转移方程为:
最后一人在队首时
if(h[l+1]>h[l]) f[l][r][0]+=f[l+1][r][0];//最后一人的前面的人来l+1~r的队头
if(h[r]>h[l]) f[l][r][0]+=f[l+1][r][1];//来l+1~r的队尾
在队尾
if(h[l]<h[r]) f[l][r][1]+=f[l][r-1][0];//来l~r-1的队头
if(h[r-1]<h[r]) f[l][r][1]+=f[l][r-1][1];//来l~r-1的队尾
枚举区间段即可。
#include <bits/stdc++.h>
using namespace std;
const int N =1e3+10,mod=19650827;
int f[N][N][2],h[N],n;
void add(int &x,int k){//计算取模
x=(x+k)%mod;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>h[i];
f[i][i][0]=1;//初始化
}
for(int len=2;len<=n;len++){//枚举区间长度,从2开始,1没必要。
for(int l=1;l+len-1<=n;l++){//枚举区间段
int r=l+len-1;
if(h[l+1]>h[l]) add(f[l][r][0],f[l+1][r][0]);
if(h[r]>h[l]) add(f[l][r][0],f[l+1][r][1]);
if(h[l]<h[r]) add(f[l][r][1],f[l][r-1][0]);
if(h[r-1]<h[r]) add(f[l][r][1],f[l][r-1][1]);
}
}
cout<<(f[1][n][0]+f[1][n][1])%mod;//总方案为最后一人来队首和队尾方案之和,取模。
return 0;
}