首页 > 其他分享 >浅谈树形dp和优化

浅谈树形dp和优化

时间：2023-03-21 15:59:42浏览次数：56  
标签：浅谈 int dfs fa 树形 MAXN 节点 dp

树是一个由 \(n\) 个节点 \(n-1\) 条边所组成的无向无环连通图。

由于每个节点只有一个父亲，可以消除在具体求解中的后效性。

一般情况下，我们会采用dfs的方式一边遍历树一边 dp。

基础树形dp

例题 \(1\)：P1352 没有上司的舞会

和序列有关的 dp 设状态一般是设成：考虑前 \(i\) 种物品……

类似的，树形 dp 设状态就会设成：考虑 \(u\) 的子树内……

这题我们也可以这么设状态：

设 \(f_{u,0/1}\) 表示考虑 \(u\) 的子树内——第二维值为 \(0\) 表示节点 \(u\) 不选，为\(1\) 表示节点 \(u\) 选时——子树内权值和的最大值。

当我们不选择节点 \(u\) 时，\(u\) 的儿子们可选可不选，则转移方程为： \(f_{u,0}=\sum\limits_{v\in \operatorname{son}(u)} \max(f_{v,0},f_{v,1})\)

当我们选择节点 \(u\) 时，\(u\) 的儿子们肯定都不能选，则转移方程为： \(f_{u,1}=r_u+\sum\limits_{v\in \operatorname{son}(u)} f_{v,0}\)

代码如下，时间复杂度 \(O(n)\):

#include<bits/stdc++.h>
using namespace std;
const int MAXN=6006;
vector<int>ve[MAXN];
int n,r[MAXN],fa[MAXN],f[MAXN][2];
void dfs(int u) {//树形dp部分
	f[u][0]=0,f[u][1]=r[u];
	for(int v:ve[u])//遍历儿子
		if(v!=fa[u]) {
			dfs(v);
			f[u][0]+=max(f[v][0],f[v][1]);
			f[u][1]+=f[v][0];
		}
}
int main() {
	scanf("%d",&n);
	for(int i=1; i<=n; ++i) 
		scanf("%d",&r[i]);
	for(int i=1,u,v; i<n; ++i) {
		scanf("%d%d",&u,&v);
		fa[u]=v,ve[v].push_back(u);
	}
	for(int i=1; i<=n; ++i)
		if(!fa[i]) {//找到根节点
			dfs(i);
			printf("%d\n",max(f[i][0],f[i][1]));
			return 0;
		}
	return 0;
}

事实上，如果用类似例题 \(2\) 的思想，我们可以把转移方程写成如下形式：

\(f^{\prime}_{u,0}\leftarrow f_{u,0}+\max(f_{v,0},f_{v,1})\)

\(f^{\prime}_{u,1}\leftarrow f_{u,1}+f_{v,0}\)

虽然代码实现还是完全一样，但是树形 dp 的转移式还是更适合写成这种依次考虑儿子的形式。

相关练习：

树上背包

例题 \(2\)：P2014 [CTSC1997] 选课

这题和例题 \(1\) 略有不同，如果设的状态只和当前节点 \(u\) 是否被选有关，是无法处理总共选 \(m\) 个点的限制的。

也就是说，我们设的状态要包括 \(u\) 整个子树内的信息。

回忆一下P1048 [NOIP2005 普及组] 采药：

我们设 \(f_{t}\) 表示用 \(t\) 的时间最多能采多少药，并且依次考虑每一种药，得到转移方程 \(f^{\prime}_{t}\leftarrow f_{t-v_i}+c_i\)。

相似的，设 \(f_{u,k}\) 表示 \(u\) 的子树内有 \(k\) 个点被选时这 \(k\) 个点的点权之和的最大值。

转移也是类似的，依次考虑 \(u\) 的每一个儿子：

设当前考虑的 \(u\) 的儿子为 \(v\)，则有转移方程：\(f^{\prime}_{u,j+k} \leftarrow f_{u,j}+f_{v,k}\)

由于选一个非根节点一定要选它的父亲节点，所以转移时要保证 \(j\geq1\)，这样一定会选上 \(u\)。

另外这题可以多建一个 \(0\) 号节点，它的权值为 \(0\)，方便计算。

代码如下，时间复杂度 \(O(n^2)\)：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=305;
int f[MAXN][MAXN],n,m,fa[MAXN],siz[MAXN],v[MAXN],tmp[MAXN];
vector<int>ve[MAXN];
void dfs(int u) {//树形dp部分
	f[u][1]=v[u];//先选上u自己
	siz[u]=1;//同时计算子树大小
	for(int v:ve[u])
		if(v^fa[u]) {
			dfs(v);//用tmp[j]暂时先存新的f[u][j]的值
			for(int j=1; j<=siz[u]; ++j)
				for(int k=0; k<=siz[v]; ++k)
					tmp[j+k]=max(tmp[j+k],f[u][j]+f[v][k]);//背包部分
			siz[u]+=siz[v];
			for(int j=1; j<=siz[u]; ++j) {//把新的值和原来的值合并
				f[u][j]=max(f[u][j],tmp[j]);
				tmp[j]=0;//记得清空
			}
		}
}
int main() {
	scanf("%d%d",&n,&m);
	for(int i=1; i<=n; ++i) {
		scanf("%d%d",&fa[i],&v[i]);
		ve[fa[i]].push_back(i);
	}
	dfs(0);
	printf("%d\n",f[0][m+1]);
	return 0;
}

我口胡了一个关于这个树上背包时间复杂度是 \(O(n^2)\) 的一个简短证明：（不想看可跳过）

设 \(T(u)\) 表示计算子树 \(u\) 内的 dp 的时间复杂度，下证命题\(P\)： \(T(u)=O(\operatorname{size}^2(u))\)

当 \(u\) 为叶子节点时，显然成立。

当 \(u\) 不为叶子节点且其儿子节点满足命题 \(P\) 时：

设 \(u\) 的儿子为 \(v_1,v_2,\cdots v_k\)，则有：

\(T(u)\\=1+\sum\limits_{i=1}^k T(v_i)+\sum\limits_{i=1}^k \operatorname{size}(v_i)(1+\sum\limits_{j=1}^{i-1}\operatorname{size}(v_i))\\<1^2+\sum\limits_{i=1}^k O(\operatorname{size}^2(v_i))+2\sum\limits_{i=1}^k \operatorname{size}(v_i)(1+\sum\limits_{j=1}^{i-1}\operatorname{size}(v_i))\\=O((1+\sum\limits_{i=1}^k \operatorname{size}(v_i))^2)\\=O(\operatorname{size}^2(u))\)

综上所述，所有树上的节点都满足命题 \(P\)，故树上背包的时间复杂度是 \(O(n^2)\) 的。

相关练习：

换根dp

例题 \(3\)：P3478 [POI2008] STA-Station

这题和前面的例题显然不同的一点是我们需要对每个节点都计算出它为根时的答案。

显然有枚举根跑 \(n\) 次 dfs，时间复杂度 \(O(n^2)\) 的做法。

我们考虑先计算出一个节点的答案，通过它的答案推出别的点的答案。

这题我们先令 \(1\) 为根并且 \(O(n)\) 算出此时的答案。

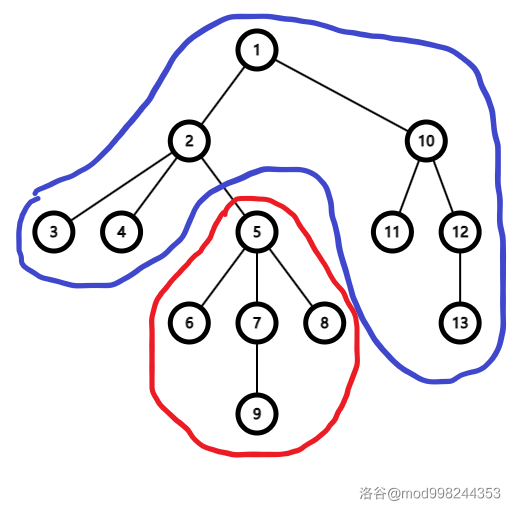
我们来比较一下根从 \(fa[x]\) 变成 \(x\) 时对答案的贡献。（注：这个父子关系是根为 \(1\) 时的）

看图可以发现以下几点：（以 \(x=5,fa[x]=2\) 为例）

  • 在 \(x\) 的子树内（即红色的部分）所有的节点到根的路径少了 \(x\) 到 \(fa[x]\) 的边，所以它们的深度都变少了 \(1\)。
  • 在 \(x\) 的子树外（即蓝色的部分）所有的节点到根的路径多了 \(fa[x]\) 到 \(x\) 的边，所以它们的深度都变多了 \(1\)。

所以我们得到递推式： \(ans[x]=ans[fa[x]]-\operatorname{size}(x)+(n-\operatorname{size}(x))\)

这样我们写两个 dfs 即可解决问题，时间复杂度 \(O(n)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=1000005;
vector<int>ve[MAXN];
int n,fa[MAXN],siz[MAXN],dep[MAXN],ans;
ll f[MAXN];
void dfs(int u) {//计算1的答案
    f[1]+=dep[u];
	siz[u]=1;
    for(int v:ve[u])
        if(v!=fa[u]) {
            fa[v]=u;
            dep[v]=dep[u]+1;
            dfs(v);
            siz[u]+=siz[v];
        }
}
void dfs2(int u) {//计算别的点的答案
    if(f[u]>f[ans]) ans=u;
    for(int v:ve[u])
        if(v!=fa[u]) {//递推式
            f[v]=f[u]+n-siz[v]-siz[v];
            dfs2(v);
        }
}
int main() {
    scanf("%d",&n),ans=1;
    for(int i=1,u,v; i<n; ++i) {
        scanf("%d%d",&u,&v);
        ve[u].push_back(v),ve[v].push_back(u);
    }
    dfs(1),dfs2(1);
    printf("%d\n",ans);
    return 0;
}

相关练习：

线段树合并优化树形dp

例题 \(4\)：CF1455G Forbidden Value

序列上的区间嵌套问题是树形的结构，我们可以把每一个操作看做一个节点：

  • 如果是 set 操作，那么它就是叶子节点。
  • 如果是 if …… end 操作，那么它中间的那些节点就是它的儿子节点

我们在最外层加一个 if 0 …… end 操作就可以转化成一颗树了。

设 \(f_{u,y}\) 表示跑完节点 \(u\) 的子树的操作后 \(x=y\) 时的最小代价。

依次考虑 \(u\) 的每个儿子 \(v\)：

  • 若 \(v\) 为 set 操作，那么转移为：\(\begin{cases}f^{\prime}_{u,y}=\min f_{u,z}\\f^{\prime}_{u,z}= f_{u,z}+val_v(y\not=z)\end{cases}\)

  • 若 \(v\) 为 if …… end 操作，那么转移为：\(\begin{cases}f^{\prime}_{u,y}=f_{u,y}+f_{v,y}\\f^{\prime}_{u,z}=\min(f_{u,z},f_{u,y}+f_{v,z})(y\not=z)\end{cases}\)

我们可以对每个节点开一颗值域线段树：

维护支持合并、单点查询 \(f_{u,y}\)、全局查询 \(f_{u,y}\) 最小值、可合并的线段树。

时空复杂度是 \(O(n\log n)\)的：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=200005;
int fa[MAXN],n,s,tcnt,t,b[MAXN],op[MAXN],y[MAXN],rt[MAXN];
ll val[MAXN];
vector<int>ve[MAXN];
struct Tree {
	int ls,rs;
	ll sum,lt;
} tr[MAXN<<5];
inline void push_up(int num) {
	tr[num].sum=min(tr[tr[num].ls].sum,tr[tr[num].rs].sum);
}
inline void upd(int num,ll val) {
	if(num)tr[num].sum+=val,tr[num].lt+=val;
}
inline void push_down(int num) {
	if(!tr[num].lt) return;
	upd(tr[num].ls,tr[num].lt),upd(tr[num].rs,tr[num].lt);
	tr[num].lt=0;
}
void update(int&num,int l,int r,int x,ll val) {
	if(!num) num=++tcnt;
	if(l==r) {
		tr[num].sum=val;
		return;
	}
	push_down(num);
	const int mid=l+r>>1;
	if(x<=mid) update(tr[num].ls,l,mid,x,val);
	else update(tr[num].rs,mid+1,r,x,val);
	push_up(num);
}
ll query(int num,int l,int r,int x) {
	if(!num) return 4e18;
	if(l==r) return tr[num].sum;
	push_down(num);
	const int mid=l+r>>1;
	if(x<=mid) return query(tr[num].ls,l,mid,x);
	return query(tr[num].rs,mid+1,r,x);
}
int merge(int num,int pre,int l,int r) {
	if(!num||!pre) return num|pre;
	if(l==r) {
		tr[num].sum=min(tr[num].sum,tr[pre].sum);
		return num;
	}
	push_down(num),push_down(pre);
	const int mid=l+r>>1;
	tr[num].ls=merge(tr[num].ls,tr[pre].ls,l,mid);
	tr[num].rs=merge(tr[num].rs,tr[pre].rs,mid+1,r);
	return push_up(num),num;
}//以上为线段树合并板子
void dfs(int u) {
	if(y[u]!=s)update(rt[u],1,t,y[u],0ll);//特判s
	for(int v:ve[u]) {
		if(op[v]==1) {
			ll tmp=tr[rt[u]].sum;
			upd(rt[u],val[v]);
			if(y[v]!=s) update(rt[u],1,t,y[v],tmp);//特判s
		} else {
			ll tmp=query(rt[u],1,t,y[v]);
			if(tmp<4e18) {
				dfs(v);
				upd(rt[v],tmp);
				update(rt[u],1,t,y[v],4e18);
				rt[u]=merge(rt[u],rt[v],1,t);
			}
		}
	}
}
char str[5];
int main() {
	scanf("%d%d",&n,&s),b[1]=0,b[t=2]=s,tr[0].sum=4e18;
	for(int i=1,x=0; i<=n; ++i) {//建树部分,x为当前节点
		scanf("%s",str);
		if(*str=='s') {
			op[i]=1,scanf("%d%lld",&y[i],&val[i]);
			fa[i]=x,ve[x].push_back(i);
			b[++t]=y[i];
		} else if(*str=='i') {
			op[i]=2,scanf("%d",&y[i]),b[++t]=y[i];
			fa[i]=x,ve[x].push_back(i),x=i;
		} else {
			x=fa[x];
		}
	}
	sort(b+1,b+t+1),t=unique(b+1,b+t+1)-b-1;
	for(int i=0; i<=n; ++i)y[i]=lower_bound(b+1,b+t+1,y[i])-b; 
	s=lower_bound(b+1,b+t+1,s)-b;//离散化
	dfs(0);
	printf("%lld\n",tr[rt[0]].sum);
	return 0;
}

相关习题：

特殊dp优化

dp优化没有固定套路，需要依据情况选择优化。

例题 \(5\)：（不公开来源）

给你一个 \(n\) 个节点的树，找到两个同构且不包含相同节点的连通块，最大化其中一个连通块的大小，\(1\leq n\leq60\)。

在一种合法方案下，一定可以删掉一条树边使原树变成两棵树且两个连通块在不同的树内。

那么，我们可以枚举原树的根 \(u\)，再枚举非根的节点 \(v\) 表示删掉的是 \(v\) 和 \(v\) 的父亲的边，并强制 \(u\) 和 \(v\) 为两个连通块的根。

那么就可以设如下的树形 dp 状态：

设 \(f_{u,v}\) 表示只考虑 \(u\) 和 \(v\) 的子树，满足两个连通块同构时其中一个连通块的大小。

转移时，显然 \(u\) 的任意儿子可以匹配 \(v\) 的任意儿子。

那么自然就是一个二分图带权最大匹配，可以用最小费用最大流做到 \(O(n^2\sqrt n)\) 转移。

由于一开始枚举是 \(O(n^2)\) 的，状态有 \(O(n^2)\) 个，故时间复杂度应为 \(O(n^{6.5})\)。

由于常数较小，在最小费用最大流求法常数优秀时每个点可以 \(20\operatorname{ms}\) 内跑出来：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=65;
int n,fa[MAXN],f[MAXN][MAXN],ans,s,t;
vector<int>ve[MAXN],son[MAXN];
int head[MAXN],ecnt,cur[MAXN],dis[MAXN],dep[MAXN];
struct Edge {
    int v,w,f,next;
} edge[200000];
inline void addedge(int u,int v,int w,int f) {
    edge[ecnt]= {v,w,f,head[u]},head[u]=ecnt++;
}
inline void Add(int u,int v,int w,int f) {
    addedge(u,v,w,f),addedge(v,u,-w,0);
}
queue<int>q;
bool vis[MAXN];
inline bool spfa() {
    for(int i=1; i<=t; ++i) {
        cur[i]=head[i];
        dis[i]=0x3f3f3f3f;
        vis[i]=false;
    }
    vis[s]=true,q.push(s),dis[s]=dep[s]=0;
    while(!q.empty()) {
        int u=q.front();
        q.pop(),vis[u]=false;
        for(int i=head[u],v; ~i; i=edge[i].next) {
            v=edge[i].v;
            if(edge[i].f&&dis[v]>dis[u]+edge[i].w) {
                dis[v]=dis[u]+edge[i].w,dep[v]=dep[u]+1;
                if(!vis[v]) q.push(v),vis[v]=true;
            }
        }
    }
    return dis[t]<0x3f3f3f3f;
}
int dfs(int u,int flow,int&res) {
    if(u==t) return flow;
    int del=flow,d=0;
    for(int i=cur[u],v; ~i&&del; i=edge[i].next) {
        v=edge[i].v,cur[u]=i;
        if(edge[i].f&&dep[v]==dep[u]+1&&dis[v]==dis[u]+edge[i].w) {
            d=dfs(v,min(del,edge[i].f),res);
            edge[i].f-=d,edge[i^1].f+=d,res-=d*edge[i].w,del-=d;
        }
    }
    if(flow==del) dep[u]=0;
    return flow-del;
}//以上为最小费用最大流板子
int solve(int x,int y,int Y) {//转移部分，Y表示删的是Y和fa[Y]的边
    if(f[x][y]) return f[x][y];
    vector<int> xson,&yson=son[y];
    for(int v:son[x]) if(v^Y)xson.push_back(v);
    f[x][y]=1;
    if(!xson.size()||!yson.size()) return f[x][y];
    for(int u:xson)
        for(int v:yson)
            solve(u,v,Y);//注意要先递归再建图
    ecnt=0,memset(head,-1,sizeof(head)),s=xson.size()+yson.size()+1,t=s+1;
    for(int i=0; i<xson.size(); ++i) Add(s,i+1,0,1);
    for(int i=0; i<yson.size(); ++i) Add(i+1+xson.size(),t,0,1);
    for(int i=0; i<xson.size(); ++i)
        for(int j=0; j<yson.size(); ++j)
            Add(i+1,j+1+xson.size(),-f[xson[i]][yson[j]],1);
    while(spfa()) dfs(s,2e9,f[x][y]);
    return f[x][y];
}
void dfs1(int u) {//处理树的基本信息
    son[u].clear();
    for(int v:ve[u])
        if(v^fa[u]) {
            son[u].push_back(v);
            fa[v]=u;
            dfs1(v);
        }
}
int main() {
    scanf("%d",&n);
    for(int i=1,u,v; i<n; ++i) {
        scanf("%d%d",&u,&v);
        ve[u].push_back(v),ve[v].push_back(u);
    }
    for(int i=1; i<=n; ++i) {
        fa[i]=0,dfs1(i);
        for(int j=1; j<=n; ++j)
            if(i^j) {
                memset(f,0,sizeof(f));
                ans=max(ans,solve(i,j,j));
            }
    }
    printf("%d\n",ans);
    return 0;
}

标签：浅谈,int,dfs,fa,树形,MAXN,节点,dp
From： https://www.cnblogs.com/mod998244353/p/17240272.html

相关文章

  • 【数位DP】计数问题
    导读^_^数位DP数位DP，即是对数的每一位进行统计操作的DP问题。计数问题思路（分类讨论）首先，如果一遍遍枚举，显示是不行的，因为1e8次这样，明显会超时。这类问题的关键是......
  • 浅谈分布式环境下WebSocket消息共享问题
    浅谈分布式环境下WebSocket消息共享问题技术分析我们在开发时会遇到需要使用即时通讯的场景，当然，实现方式很多，Socket、MQTT、Netty....等等。具体用哪种就在于业务的需求......
  • DP 与 DDP
    前言​ DP与DDP均为GPU并行手段，目的是加快训练。DP(Dataparallelism)如上图所示：DP其实只开了一个线程，并行算法实在多个设备上都拷贝了一份完整的模型参数，彼此之......
  • Closure Table如何将树形结构存储在数据库中
    今天介绍将树形结构存储在数据库中的第三种方法——闭包表ClosureTable继续用上一篇的栗子，下面是要存储的结构图：需要回答的问题依旧是这样几个：1.查询小天的直......
  • [浅谈] 二维数据结构——树套树
    \(\color{purple}\text{Ⅰ.二维树状数组}\)\(\color{orange}\text{例一：P3372【模板】线段树1}\)$\color{green}\text{2023.1.1014:32}$回忆一下树状数组的区间修改......
  • [浅谈] 线段树优化建边
    \(\color{purple}\text{P6348[PA2011]Journeys}\)\(\color{green}\text{2023.1.1010:58}\)线段树优化建边。题意：给定一个图，每次对区间\([a,b]\)至区间\([c,d]\)建......
  • 浅谈集合HashSet
    HashSet简介HashSet集合继承于Collection集合，Collection集合的常用方法也在HashSet中同样适用。底层原理：HashSet集合底层采用哈希表存储数据，底层是new了一个HashMap，a......
  • udp编程实例1
    #include<signal.h>#include<stdio.h>#include<errno.h>#include<unistd.h>#include<stdlib.h>#include<time.h>#include<string.h>#include<arpa/inet.h>......
  • 「线性DP」乘积最大
    本题为3月20日23上半学期集训每日一题中A题的题解题面题目描述今年是国际数学联盟确定的“2000——世界数学年”，又恰逢我国著名数学家华罗庚先生诞辰90周年。在华罗庚......
  • 【洛谷】P4590 [TJOI2018]游园会（dp套dp）
    原题链接题意对于一个长度为\(n\)的仅由\(N,O,I\)组成且不包含字串\(NOI\)的字符串\(S\)，其与一个给定的长度为\(K\)的字符串的最长公共子序列为\(LCS\)。求出......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99