1 前言
声明:本博客里的数组乘法运算是指矩阵乘法运算,不是对应元素相乘。
在线性代数或高等代数中,我们学习了矩阵乘法,那么,什么样的高维数组才能相乘?tensorflow 又是如何定义高维数组运算规则?
2 运算条件
- 两数组的维数相同:len(a.shape)=len(b.shape)
- 前n-2个维度都一致:a.shape[0]=b.shape[0],...,a.shape[-3]=b.shape[-3]
- 最后两个维度满足矩阵乘法运算:a.shape[-1]=b.shape[-2]
假设 a.shape=(n1,n2,...,nL),b.shape=(m1,m2,...,mL),则 tf.matmul(a,b) 能运算的条件如下图(箭头表示相等):
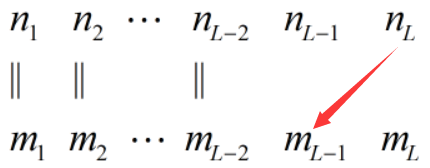
3 运算规则
令 c=tf.matmul(a,b),因为a和b只有最后两维不一致,若以二维矩阵为最小的元素,则a和b的维数完全一致,c的每个元素为a和b的对应元素相乘,每个元素都是一个二维矩阵。
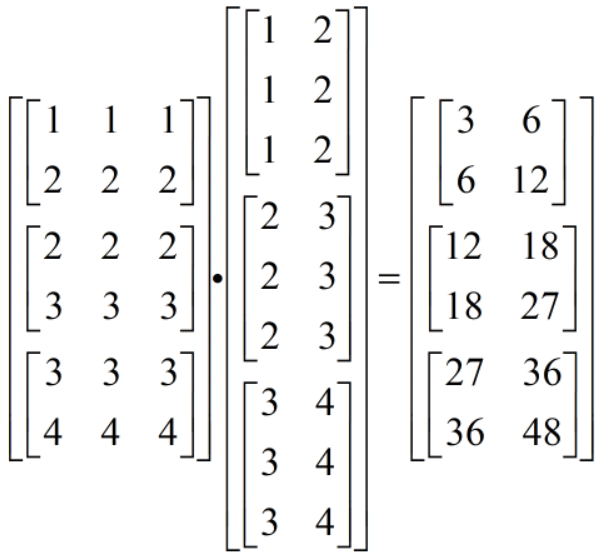
4 实验
import numpy as np
import tensorflow as tf
a=np.array(
[[[1,1,1],
[2,2,2]],
[[2,2,2],
[3,3,3]],
[[3,3,3],
[4,4,4]]])
b=np.array(
[[[1,2],
[1,2],
[1,2]],
[[2,3],
[2,3],
[2,3]],
[[3,4],
[3,4],
[3,4]]])
c=tf.matmul(a,b)
with tf.Session() as sess:
c=sess.run(c)
print("c=tf.matmul(a,b)\n",c)
c=tf.matmul(a,b)
[[[ 3 6]
[ 6 12]]
[[12 18]
[18 27]]
[[27 36]
[36 48]]]
声明:本文转自tensorflow中高维数组乘法运算
标签:运算,matmul,shape,tf,tensorflow,高维,乘法 From: https://www.cnblogs.com/zhyan8/p/17232657.html