论文:https://gitee.com/ss-Payne/paper/blob/master/Calibration/Simultaneous_Calibration_of_Odometry_and_Sensor_Parameters_for_Mobile_Robots.pdf
代码:https://github.com/MegviiRobot/OdomLaserCalibraTool
期刊:IEEE Transactions on Robotics, 29, 475-492
概述
在分析了该问题的可观测性后,本文提出了一种不需要额外的外部传感器或设备,只需要测量车轮速度和外部感受传感器的数据,即可同时校准所有参数的方法。此外,该方法不需要机器人沿着特定的轨迹移动。将同时标定问题表示为极大似然问题,并求闭式解。实验结果表明,该标定方法的精度非常接近可达到的极限。
介绍
里程计校准的相关工作
方法一
最流行的方法包括沿着特别设计的轨迹驱动机器人,通过外部传感器对其姿态进行一些外部测量,然后根据关于在估计的参数会影响最终的姿势。
方法二
将里程计校准制定为过滤问题。一种可能性是使用扩展卡尔曼滤波器(EKF)来估计机器人的姿势和里程计参数
方法三
过滤的替代方法是解决优化问题,通常采用最大似然估计的形式。使用最大似然法:估计差速驱动机器人的里程参数,使用外部摄像机的绝对观测。这个该方法特别简单,因为问题是精确线性的,因此可以用线性最小二乘法求解。
外部传感器标定相关工作
外部传感器标定时会存在不可避免的尺度不确定性,系统不能完全被观测到。
同时校准里程表和外感受传感器
在《Automatic Calibration of Multiple Coplanar Sensors》中提出的方法有几个有趣的特点:机器人沿着任意轨迹自主驱动,不需要外部测量,也不需要事先测量标称参数。此外,作为一个静态最大似然问题的公式允许检测和过滤异常值。
本论文是该工作的延伸。对于原论文,给出了一个非线性和随机可观测性分析,证明了系统是局部可观测的,以及全局对称性的一个完整刻画
问题表述
SE(2)是平面运动的特殊欧式群,se(2)是其相应的李代数。假设: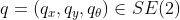 ,作为机器人相对于固定的世界坐标系的一个姿态。对于差速机器人,可以根据微分方程进行变化:
,作为机器人相对于固定的世界坐标系的一个姿态。对于差速机器人,可以根据微分方程进行变化:
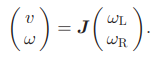
驱动速度 和转向速度
和转向速度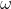 取决于左右轮差速
取决于左右轮差速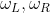 ,这里存在一个线性转换:
,这里存在一个线性转换:
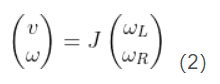
转换矩阵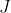 是机器人参数
是机器人参数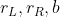 的一个函数,
的一个函数,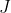 的定义如下所示:
的定义如下所示:
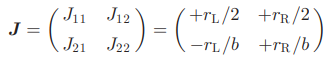
其中,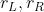 分别是左右轮的轮径,b 是左右轮的轮距。我们假设能够测量左右轮的转速
分别是左右轮的轮径,b 是左右轮的轮距。我们假设能够测量左右轮的转速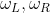 。我们不假定能够设定车轮速度;这种方法是完全被动的。如果它满足必要的兴奋性条件,可以适用于任何轨迹,在下一节概述。
。我们不假定能够设定车轮速度;这种方法是完全被动的。如果它满足必要的兴奋性条件,可以适用于任何轨迹,在下一节概述。
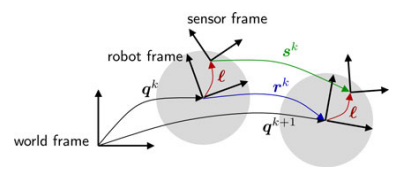
我们还假设在机器人平台上有一个水平安装的外感受传感器(俯仰和横滚为零,只感受偏航)。在此基础之上,传感器相对于机器人参考系的位姿可以表示为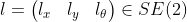 (图1所示)。因此,任意时刻 t,传感器在世界坐标系中的位姿为
(图1所示)。因此,任意时刻 t,传感器在世界坐标系中的位姿为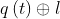 。这里
。这里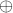 表示
表示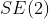 的李群运算。表1定义了
的李群运算。表1定义了 和
和 在
在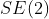 中的运算
中的运算

外在的观察自然是一个离散的过程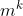 :观测可以在一组时间序列上:
:观测可以在一组时间序列上: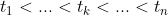 ,这组序列一般不是均匀分布的。就假如第k个时间间隔
,这组序列一般不是均匀分布的。就假如第k个时间间隔![t\in\left [ t_,t_{k+1} \right ]](https://ssrick.oss-cn-shanghai.aliyuncs.com/img/202209181818509.gif) ,假设机器人的初始和最终姿态分别为
,假设机器人的初始和最终姿态分别为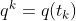 和
和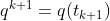 。用 sk 表示传感在区间
。用 sk 表示传感在区间![t\in\left [ t_,t_{k+1} \right ]](https://ssrick.oss-cn-shanghai.aliyuncs.com/img/202209181818756.gif) 上的位移,根据图1的运动,可以用以下方程进行描述:
上的位移,根据图1的运动,可以用以下方程进行描述:
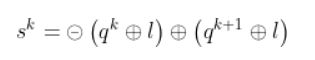
令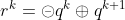 ,rk 可以表示为机器人在此时间间隔内的位移,传感器的位移进一步可以表示为(交换律):
,rk 可以表示为机器人在此时间间隔内的位移,传感器的位移进一步可以表示为(交换律):
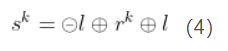
我们假设能够估计出传感器的帧间位移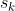 依靠与传感器捕获的外界测量值
依靠与传感器捕获的外界测量值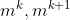 ,并且我们能用比如激光器帧间匹配的方法得到一个
,并且我们能用比如激光器帧间匹配的方法得到一个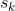 的估计
的估计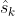 。
。
此时,待解决的问题就可以陈述为:
问题:同时校准:在时间![t\in\left [ t_{1},t_{k+1} \right ]](https://ssrick.oss-cn-shanghai.aliyuncs.com/img/202209181821532.gif) 区间内给定两个车轮转速
区间内给定两个车轮转速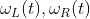 ,以及与外部在时间序列
,以及与外部在时间序列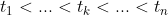 上的传感器观测估计
上的传感器观测估计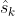 ,为
,为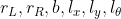 找到最大似然估计值。
找到最大似然估计值。
不难发现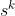 就是带估计值的函数。
就是带估计值的函数。
计算方法
假设
- sk 的方差 ∑k 是对角矩阵且在x和y方向是各向同性的。
算法概述
J21,J22的线性估计
其他参数的非线性估计
异常值去除
不确定性估计
恒定轮速的更简单公式
结论
本文提出了一种简单实用的同时标定差动驱动机器人的里程表参数和安装在机器人上的外感受传感器的外位姿的方法。该方法有一些有趣的特点:它可以在无人看管的情况下运行,无需人工干预;没有任何仪器需要预先校准;不需要标称参数作为初始猜测,全局最优解以封闭形式存在;机器人的轨迹可以自由选择,只要它们激活所有的参数。我们有实验评价方法在移动平台上配备了激光测距仪放置在各种配置,使用扫描匹配作为传感器位移估计方法,我们已经表明,校准精度与理论极限的Cramér Rao bound。
标签:Odometry,Calibration,机器人,校准,估计,Simultaneous,参数,传感器,方法 From: https://www.cnblogs.com/ss-Rick/p/16705491.html