在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合 ,最早来自于方程组的系数及常数所构成的方阵。矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。

1850年,英国数学家 James Joseph Sylvester (1814-1897) 将“矩阵”(Matrix)作为术语提出,Matrix源于拉丁语“子宫”(womb之意);1855年,Sylvester和他一生的挚友Arthur Cayley (1821-1895)发表文章,首次以矩阵的形式表达线性方程组。一种强大的新的数学语言从此诞生!拉普拉斯说:简化的记法常常是深奥理论的源泉,举个略夸张的例子:有人说莱布尼茨的微分表示法\(\frac{dy}{dx}\)使欧洲微积分领先使用牛顿记法 $ \dot x$的英国100年。深度学习本质上特征学习,良好的的表达形式非常重要!
一 矩阵的引入
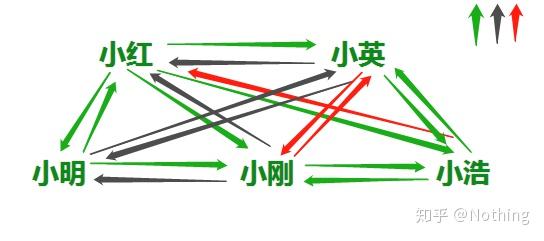
绿色「1」表示认识
黑色「2」表示不认识,
红色「3」代表喜欢「也就是暗恋呀」
天哪,看这个也更晕了!!!!!快给我看看矩阵是怎样的??
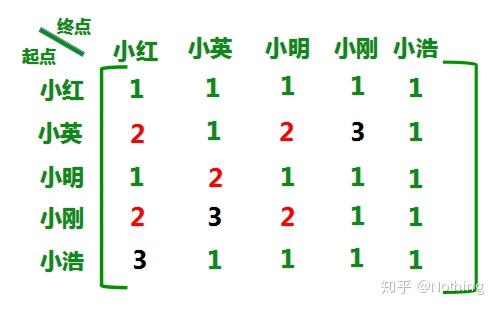
矩阵看起来就方便很多,就连调查一个人的关系也很容易,比如我们调查一下小明,看看有谁认识他,看看他认识谁。。
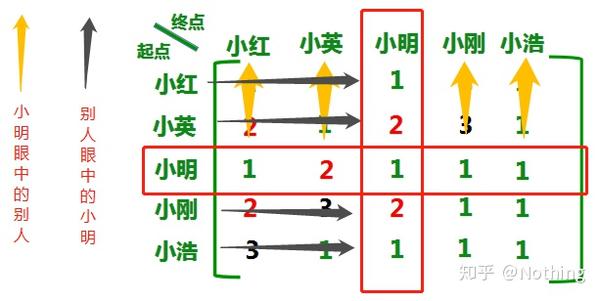
你看,这是不是就清晰许多了?所以矩阵的用处是灰常灰常广泛的,也是很好用的一种统计与调差方法。。
矩阵的定义:
由$ m×n $个数 $ a_{ij} $ 排成的 \(m\) 行 \(n\) 列的数表称为\(m\)行\(n\)列的矩阵,简称\(m × n\)矩阵,其中\(m\)为行数、\(n\)为列数。

二 矩阵和线性方程组
Cayley是第一个把矩阵作为独立的对象进行研究的人。1858年,他发表了矩阵领域里程碑文章 Memoir on the Theory of Matrices,定义了今天行列式的表示法、矩阵加法、数乘、乘法、次方、单位矩阵、零矩阵和逆矩阵,Cayley-Hamilton定理达到了顶峰,他被公认为矩阵的创立者。Cayley是一位高产数学家,与他在群论、图论和不变量理论方面的贡献相比,线代方面的贡献被掩盖了,而且,很多工作是在十几年律师生涯中利用业余时间做的。
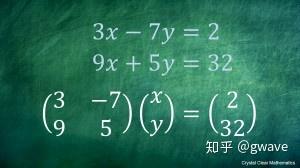
2.1 线性方程组矩阵表达
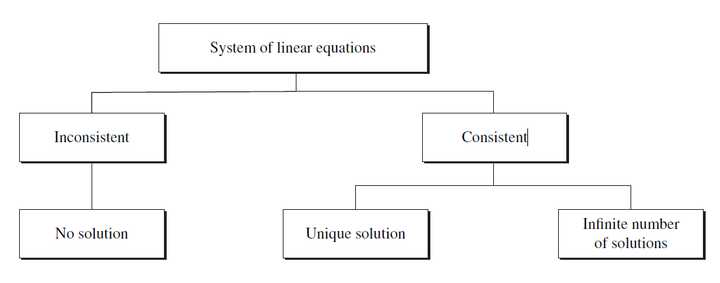
任何一个方程组解的情况:
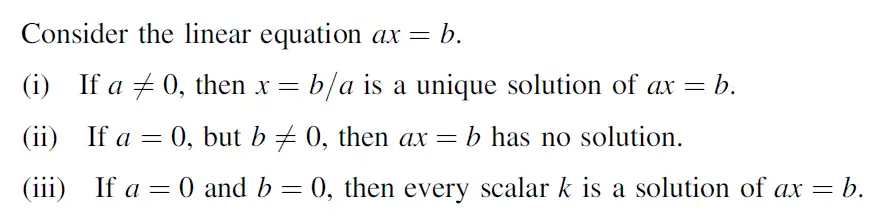
判断两个方程组是否有相同解:
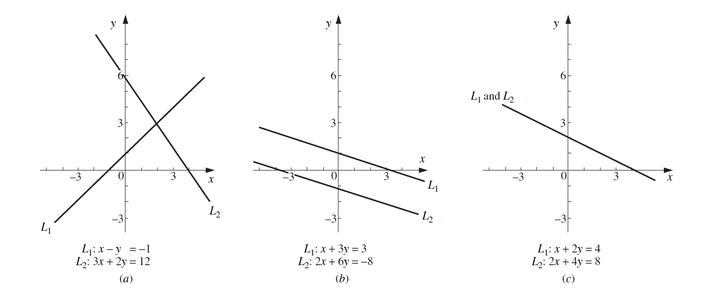
图(a)表示, 两个方程组只在交点处有相同解.
图(b)表示, 两个方程组在R都没有相同解
图(c)表示, 两个方程组在R的处处都有相同解
2.2 从行的角度思考
学习了矩阵、向量的表示方法以及运算规则之后,我们回过头来静静的思考一个问题:矩阵 \(A\)和列向量\(x\) 的乘法 \(Ax\) 到底意味着什么?下面,我们就来挖掘一下这里面的内涵。
在二阶方阵 \(A\)与二维列向量\(x\)相乘的例子中,
\[Ax= \begin{bmatrix} a & b \\c &d \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} =\begin{bmatrix} ax_1 +bx_2 \\ cx_1+dx_2 \end{bmatrix} \]刚才说了,位于矩阵\(A\) 第 \(i\) 行的各元素和列向量 \(i\) 各成分分别相乘后相加,得到的就是结果向量的第\(i\)个成分。这个计算方法有没有感觉很熟悉?没错,这不就是向量点乘的定义式么?
即:
\[Ax=\begin{bmatrix} row_1 \\ row_2 \end{bmatrix} x= \begin{bmatrix} row_1 \cdot x\\ row_2 \cdot x\end{bmatrix} \]矩阵与向量的乘法如果从行的角度来看,就是如此。常规的计算操作就是这么执行的,但是似乎也没有更多可以挖掘的,那我们试试继续从列的角度再来看看。
2.3 列的角度:重新组合矩阵的列向量
如果从列的角度来计算矩阵与向量的乘积,会有另一套计算的方法,可能大家对这种方法要相对陌生一些。但是实质上,这种方法从线性代数的角度来看,还要更为重要一些,我们还是用二阶方阵进行举例。
\[Ax= \begin{bmatrix} a & b \\ c &d \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} =x_1\begin{bmatrix} a\\ c\end{bmatrix} +x_2\begin{bmatrix} b\\ d\end{bmatrix} =\begin{bmatrix} ax_1 +bx_2 \\ cx_1+dx_2 \end{bmatrix} \]发现了规律没有?我们通过这种形式的拆解,也能得到最终的正确结果,这就是从列的角度进行的分析。从前面的知识我们可以这样描述:从列的角度来看,矩阵 \(A\) 与向量\(x\) 的乘法是对矩阵\(A\) 的各列向量进行线性组合的过程,每个列向量的组合系数就是向量 \(x\) 的各对应元素。
这么理解似乎有点新意,我们按照列的思想重新把矩阵\(A\)写成一组列向量的形式:
依照上述公式,我们举一个实际的例子,就更清楚了。
\[Ax=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 3 \\ 5 \end{bmatrix} =3\begin{bmatrix} 1\\ 3\end{bmatrix} +5\begin{bmatrix} 2\\ 4\end{bmatrix} \]所得到的结果就是矩阵第一列的列向量$ \begin{bmatrix} 1\\ 3\end{bmatrix}$ 的3倍加上第二列列向量 \(\begin{bmatrix} 2\\ 4\end{bmatrix}\) 的5倍。
因此,一个矩阵和一个向量相乘的过程,就是对位于原矩阵各列的列向量重新进行线性组合的过程,而线性组合的各系数就是向量的对应各元素。
三 矩阵和表
产品分析是数据分析永远绕不开的一环,但是很多人在对产品进行分析的时候,会因为无从下手而产生很多疑问,比如怎么分析每一种产品对于用户的吸引力?如何衡量产品的比重?如何准确掌握产品更迭速度?如何对其进行有计划的投入呢?典型例子比如某家手机品牌,其旗下手机的品种档次很多,而手机产品更迭速度之快也不用多说,为了实现品牌的差异化必然要不断推出新品,这就带来了问题:究竟是要大量投入新品还是旧品呢?如果投入的产品根本不受欢迎,就会血本无归,这也是很多电商面临的问题。
数据分析模型——波士顿矩阵,正可以完美解决这个问题!波士顿矩阵(BCG Matrix),又称市场增长率-相对市场份额矩阵,由美国著名的管理学家、波士顿咨询公司创始人布鲁斯·亨德森于1970年首创,它是通过销售增长率(反应市场引力的指标)和市场占有率(反应企业实力的指标)来分析决定企业的产品结构。市场吸引力包括企业销售量增长率、目标市场容量、竞争对手强弱、利润高低等。其中最重要的是反映市场引力的综合指标——销售增长率,这是决定企业产品结构是否合理的外在因素。企业实力包括市场占有率、技术、设备、资金利用能力等,其中市场占有率是决定企业产品结构的内在因素,他直接显示出企业的竞争实力。

波士顿矩阵将产品类型分为四种:
明星类产品:高增长且高市占,发展前景好,竞争力强,需加大投资以支持其发展;
问题类产品:高增长但低市占,发展前景好但市场开拓不足,需谨慎投资;
现金牛产品:低增长但高市占,成熟市场的领导者,应降低投资,维持市占并延缓衰退;
瘦狗类产品:低增长且低市占,理论率低甚至亏损,应采取撤退战略。
四 矩阵和数组
计算机中对于矩阵,我们一下想到的就是C语言中的二维数组,这个是满足矩阵结构的一种数据结构。但是矩阵的应用远不止这些。对于数值计算,大量的方程组求解,图像的压缩,求多项式函数的数值解等等,都是矩阵在数据处理中的出彩表现。
基本的二维变换可包括旋转、缩放、扭曲,和平移四种,而这些几何运算则能够转换为一些基本的矩阵运算:

总结
进入20世纪,矩阵被被广泛应用于不同领域:海森堡在量子力学中,冯诺伊曼在计算机中都开始应用了矩阵,纳什在博弈论中……。今天,机器学习更是将矩阵作为最基础的工具,矩阵运算已经成为大数据时代的加减乘除,在从现实的原子世界向虚拟的比特世界迁移中,矩阵像阳光和氧气一样无所不在。