这是一个暴力枚举题
有两种解决方法,第一种用九重for循环(有点麻烦,尽量别用),第二种简化版(虽然行数少了,但难理解),先来看看
题目!!!
题目描述
考虑将如此安排在一个 3*3 行列中的九个时钟:
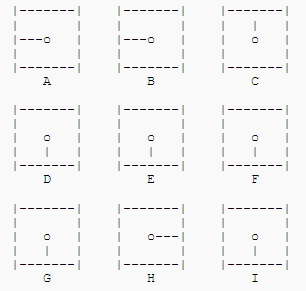
目标要找一个最小的移动顺序将所有的指针指向 12点。下面原表格列出了 9 种不同的旋转指针的方法,每一种方法都叫一次移动。
选择 1∼9 号移动方法,将会使在表格中对应的时钟的指针顺时针旋转 90度
| 移动方法 | 受影响的时钟 |
|---|---|
| 1 | ABDE |
| 2 | ABC |
| 3 | BCEF |
| 4 | ADG |
| 5 | BDEFH |
| 6 | CFI |
| 7 | DEGH |
| 8 | GHI |
| 9 | EFHI |
通过这个表格,我们可以做一个演示图来加深理解

输入格式
输入三行,每行三个正整数,表示一个时钟的初始时间,数字的含意和上面第一个例子一样。
输出格式
单独的一行包括一个用空格分开的将所有指针指向 1212 点的最短移动顺序的列表。
如果有多种方案,输出那种使其连接起来的数字最小的方案。(举例来说 5 2 4 6<9 3 1 15 2 4 6<9 3 1 1 )。
输入输出样例
输入 #1 9 9 12 6 6 6 6 3 6 输出 #1 4 5 8 9 下面,上代码~~~~~~~~#include<bits/stdc++.h>
using namespace std;
int q[10000],a[100];
int main(){
for(int i=1;i<=9;i++){
cin>>a[i];
a[i]=a[i]/3;
}
for(int k=0;k<=3;k++)
for(int b=0;b<=3;b++)
for(int c=0;c<=3;c++)
for(int d=0;d<=3;d++)
for(int e=0;e<=3;e++)
for(int f=0;f<=3;f++)
for(int g=0;g<=3;g++)
for(int h=0;h<=3;h++)
for(int i=0;i<=3;i++)
if((k+b+d)%4==(4-a[1])%4 and (k+b+c+e)%4==(4-a[2])%4 and (b+c+f)%4==(4-a[3])%4 and (k+d+e+g)%4==(4-a[4])%4 and (k+c+e+g+i)%4==(4-a[5])%4 and (c+e+f+i)%4==(4-a[6])%4 and (d+g+h)%4==(4-a[7])%4 and (e+g+h+i)%4==(4-a[8])%4 and
(f+h+i)%4==(4-a[9])%4){
q[1]=k,q[2]=b,q[3]=c,q[4]=d,q[5]=e,q[6]=f,q[7]=g,q[8]=h,q[9]=i;
for(int i=1;i<=9;i++)
if(q[i]>0){
for(int j=1;j<=q[i];j++){
cout<<i<<" ";
}
}
}
return 0;
}
这看似杂乱无章的代码,其实很简单,这不过是把初始时间挨个算出来,然后输出。
不得不说,是真的丑!!!!!
再来看看化简代码(你们自己写吧,我就不献丑了)
再回
886~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
最后叭叭几句(不会上网自己查吧)
标签:输出,移动,洛谷,表格,USACO1.4,int,IOI1994,时钟,指针 From: https://www.cnblogs.com/zsy-2010/p/17179429.html