题单
0X00 P7860 [COCI2015-2016#2] ARTUR
好题。
首先考虑本题与拓扑排序有和关系。可以想到,某些棍子的先后移动顺序是有限制的。比如:
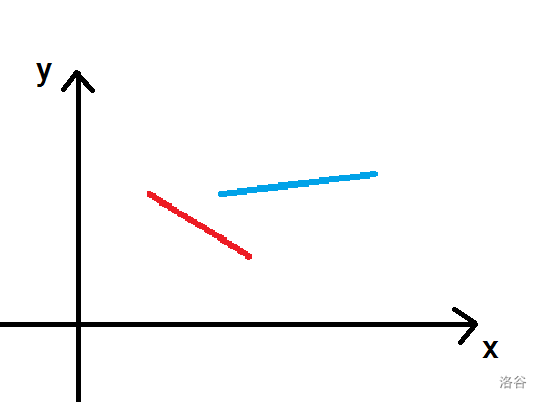
这里红色的必须比蓝色的先移动,因为它们在 \(x\) 轴的投影有重叠,蓝色在上,会被红色卡住。
所以,棍子两两之间可能存在限制关系,这就符合拓扑排序的条件了。考虑根据每一对限制关系建边。若 \(u\) 必须比 \(v\) 先移动,就从 \(u\) 向 \(v\) 连边,这样就转化为求拓扑序问题了。
其次,也是较麻烦的一部分,就是如何根据两线段的坐标判断其移动先后限制。
为了方便,在读入时判断并交换好,用 \(x1,y1\) 表示左边端点,\(x2,y2\) 表示左边端点。
\(\text {ckeck}\) 函数,分以下几种情况讨论:
- 没有限制关系,返回 \(0\)
- \(u\) 比 \(v\) 要先移动,返回 \(-1\)
- \(v\) 比 \(u\) 要先移动,返回 \(1\)
为了方便,设 \(u\) 为靠左的线段,若不是,在开始判断前将交换一下,并需要把 \(op\)(返回值)取反。
首先看 \(op=0\),即两线段在 \(x\) 轴上投影不重合:

肉眼可见,\(u.x2<v.x1\),注意等号不可以取到(照提交意思来看...)。
然后看一般情况。多画几个图,可以发现,只需要比较 \(u\) 上 \(x=v.x1\) 时 \(u.y'\) 的值与 \(v.y1\) 的大小 即可(或 \(v\) 上 \(x=u.x2\) 时 \(v.y'\) 的值与 \(u.y2\) 的大小)。在下的先移,在上的后移。

至于如何求函数值。。上过初中数学都会。程序中变量名都遵从 \(y=kx+b\) 了。
然鹅,这样写获得了 \(95\) 分的高分。哪里出问题了?
还有一种比较坑的情况,就是 \(u\) 是竖直的!

这时候函数 \(u\) 的 \(k\) 是无限大的,不是一次函数,无法求出值。所以需要特判,算出 \(x=u.x1\) 时 \(v\) 的函数值再比较。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,in[5005];
struct node{
int x1,x2,y1,y2;
}b[5005];
vector<int> a[5005];
queue<int> q;
int check(node u,node v){ //0:无关,-1:先移u,1:先移v
int op=1;
if(u.x1>v.x1) swap(u,v),op=-op;
if(u.x2<v.x1) return 0;
double K,B,tmp;
if(!(u.x2-u.x1)){
K=1.0*(v.y2-v.y1)/(v.x2-v.x1);
B=(double)v.y1-K*v.x1;
tmp=K*u.x1+B;
if(u.y1>tmp) return op;
return -op;
}
K=1.0*(u.y2-u.y1)/(u.x2-u.x1);
B=(double)u.y1-K*u.x1;
tmp=K*v.x1+B; //求函数
if(tmp>v.y1) return op;
return -op;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d%d%d",&b[i].x1,&b[i].y1,&b[i].x2,&b[i].y2);
if(b[i].x1>b[i].x2) swap(b[i].x1,b[i].x2),swap(b[i].y1,b[i].y2);
}
for(int i=1;i<n;i++){
for(int j=i+1;j<=n;j++){
int op=check(b[i],b[j]);
if(op==-1) a[i].push_back(j),in[j]++;
if(op==1) a[j].push_back(i),in[i]++; //连边
}
}
for(int i=1;i<=n;i++) if(!in[i]) q.push(i),printf("%d ",i);
while(q.size()){ //拓扑
int k=q.front();
q.pop();
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
in[tmp]--;
if(!in[tmp]) q.push(tmp),printf("%d ",tmp);
}
}
return 0;
}
0X01 UVA1423 Guess
是正号就建正向边,负号就建反向边。然后跑拓扑就可以通过每次 \(-1\) 求出前缀和数组。
最后前缀和数组两两作差即可求出一组符合条件的答案。
注意每次要清空图,同时为前缀和数组赋初值。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,in[15],T,sum[15];
char c;
vector<int> a[15];
queue<int> q;
void solve(){
for(int i=0;i<=10;i++) a[i].clear(),sum[i]=20;
scanf("%d",&n);
for(int i=0;i<n;i++){
for(int j=i+1;j<=n;j++){
cin>>c;
if(c=='+') a[j].push_back(i),in[i]++;
if(c=='-') a[i].push_back(j),in[j]++;
}
}
for(int i=0;i<=n;i++) if(!in[i]) q.push(i);
while(q.size()){
int k=q.front();q.pop();
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
sum[tmp]=sum[k]-1;
in[tmp]--;
if(!in[tmp]) q.push(tmp);
}
}
for(int i=1;i<=n;i++) printf("%d ",sum[i]-sum[i-1]);
printf("\n");
}
int main(){
scanf("%d",&T);
while(T--) solve();
return 0;
}
0X02 P1983 [NOIP2013 普及组] 车站分级
考虑以车站等级为限制要求来建边。
以一趟从 \(x\) 到 \(y\) 的列车为例,\(x \sim y\) 中没有停靠的站点的优先级一定比停靠的车站低,所以考虑在每一对停和未停的车站间建有向边。
比如样例一中 1 3 5 6:
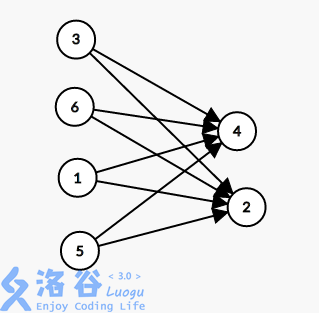
考虑到站点较多,可能重复建边,所以每次建边标记一下。
最后答案即为图的层数。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,in[1005],x,y[1005],dep[1005],ans;
bool mark[1005][1005],fl[1005];
vector<int> a[1005];
queue<int> q;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d",&x);
for(int j=1;j<=n;j++) fl[j]=0;
for(int j=1;j<=x;j++) scanf("%d",&y[j]),fl[y[j]]=1;
for(int j=y[1];j<=y[x];j++){
if(fl[j]) continue;
for(int k=1;k<=x;k++){
if(mark[j][y[k]]) continue;
a[j].push_back(y[k]);
in[y[k]]++;
mark[j][y[k]]=1;
}
}
}
for(int i=1;i<=n;i++){
if(!in[i]) q.push(i),dep[i]=1;
}
while(q.size()){
int k=q.front();q.pop();
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
dep[tmp]=max(dep[tmp],dep[k]+1);
in[tmp]--;
if(!in[tmp]) q.push(tmp);
}
}
for(int i=1;i<=n;i++) ans=max(ans,dep[i]);
printf("%d",ans);
return 0;
}
0X03 P1347 排序
因为题目要求合法就输出,所以要边输入边判断,也就是每次都跑一遍拓扑。
还好数据范围不大,完全可以。
一共存在三种情况:
- 可以确定顺序,立刻输出
- 非法,立刻停止
- 最终也无法确定顺序
这里注意,可以确定顺序 不是存在合法拓扑序,而是要合法且唯一,这就意味着吗,每个点都要在单独的一层。
非法 就是存在环,用常规判环方法,如果一次拓扑遍历到的节点少于 当前应该有的节点 ——注意是当前,每次要数已经有几个节点了——那么久非法了,直接输出并结束。
如果一次遍历到的节点达到了 \(n\),并且其层数也达到了 \(n\),那么久合法。
如果到最后既没有非法也没有合法,就是无法确定。
还有,每次拓扑的时候要先把 \(in\) 数组复制一下,直接改会出错。
以下程序中 \(kk\) 是应该有的节点数, \(cnt\) 是实际遍历到节点数,\(mx\) 是当前的层数,其他很好理解。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,in[30],ans[30],cnt,dep[30],mx,kk;
bool mark[30];
string s;
vector<int> a[30];
queue<int> q;
int topo(){
while(q.size()) q.pop();
memset(ans,0,sizeof(ans));
memset(dep,0,sizeof(dep));
mx=kk=0;
int iin[30];
for(int i=0;i<26;i++) if(mark[i]) iin[i]=in[i],kk++;
for(int i=0;i<26;i++){
if(!iin[i]&&mark[i]) q.push(i),dep[i]=1;
}
int cnt=0;
while(q.size()){
int k=q.front();q.pop();
ans[++cnt]=k;
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
dep[tmp]=dep[k]+1;
mx=max(mx,dep[tmp]);
iin[tmp]--;
if(!iin[tmp]) q.push(tmp);
}
}
if(cnt==n&&mx==n) return 1;
else if(cnt<kk) return 2;
else return 0;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
cin>>s;
int x=s[0]-'A',y=s[2]-'A';
mark[x]=mark[y]=1;
a[x].push_back(y);in[y]++;
if(topo()==1){
printf("Sorted sequence determined after %d relations: ",i);
for(int j=1;j<=n;j++) printf("%c",ans[j]+'A');
printf(".");
return 0;
}
else if(topo()==2){
printf("Inconsistency found after %d relations.",i);
return 0;
}
}
printf("Sorted sequence cannot be determined.");
return 0;
}
0X04 CF977D Divide by three, multiply by two
先将所有数两两成对判断,如果 \(b[i]\times 2=b[j]\) 或者 \(b[i] \mod 3=0\ \&\&\ b[i]\div 3=b[j]\),那么就在这两点之间连边。
然后直接跑拓扑,找到合法拓扑序即可。
Code:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,in[105],x,y,b[105];
vector<int> a[105];
queue<int> q;
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++) scanf("%lld",&b[i]);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j) continue;
if(b[i]*2==b[j]) a[i].push_back(j),in[j]++;
else if(b[i]%3==0&&b[i]/3==b[j]){
a[i].push_back(j),in[j]++;
}
}
}
for(int i=1;i<=n;i++) if(!in[i]) q.push(i);
while(q.size()){
int k=q.front();q.pop();
printf("%lld ",b[k]);
for(int i=0;i<a[k].size();i++){
in[a[k][i]]--;
if(!in[a[k][i]]) q.push(a[k][i]);
}
}
return 0;
}
0X05 CF510C Fox And Names
考虑连边方式:
将相邻的字符串两两拿出来,从第一位开始逐位向后比较,相等就跳过,不相等就要记录。
因为按“字典序”从小到大排,所以从前一个的字符串的那一位字母向后一个字符串的那一个字母连边,然后就直接 break(因为已经满足了!)。
其实可以优化,记录下已经确定的边的关系,再碰到如果符合就可以直接跳过,不符合就直接无解,但以下程序中没有写 \(qwq\)。
考虑一种特殊情况,后一个字符串是前一个的严格前缀,这样根据字典序的定义是前面的较大,但不会判断出来,所以直接标记一下无解即可。
最后就是常规的判环。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,in[35],u[105],v[105],ans[105],cnt;
string s[105];
vector<int> a[35];
queue<int> q;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) cin>>s[i];
for(int i=2;i<=n;i++){
int l1=s[i-1].size(),l2=s[i].size();
for(int j=0;j<l1;j++) u[j+1]=s[i-1][j]-'a';
for(int j=0;j<l2;j++) v[j+1]=s[i][j]-'a';
bool fl=0;
for(int j=1;j<=min(l1,l2);j++){
if(u[j]==v[j]) continue;
fl=1;
a[u[j]].push_back(v[j]);
in[v[j]]++;
break;
}
if(!fl&&l1>l2){
printf("Impossible");
return 0;
}
}
for(int i=0;i<26;i++) if(!in[i]) q.push(i);
while(q.size()){
int k=q.front();q.pop();
ans[++cnt]=k;
for(int i=0;i<a[k].size();i++){
in[a[k][i]]--;
if(!in[a[k][i]]) q.push(a[k][i]);
}
}
if(cnt<26){
printf("Impossible");
return 0;
}
for(int i=1;i<=26;i++) printf("%c",ans[i]+'a');
return 0;
}
0X06 AT1726 Dictionary for Shiritori Game
初看就是普通拓扑,其实比较有技巧。
要判断先后手必胜情况比较麻烦。考虑以下几种情况(设 \(ans_i=1\) 必败,\(ans_i=2\) 必胜):

容易想到,没有出度的点 \(3\) 必败,而可以直接到达点 \(3\) 的点 \(1\) 和点 \(2\) 必胜。
看 \(4\),他可以到达 \(1\) 和 \(2\) 都是必胜,那么他无论走向 \(1\) 还是 \(2\) 都是必败的。
再看 \(5\),虽然他走向 \(2\) 会失败,但他一定会选择走向点 \(4\),使对手必败,所以他还是必胜的。
从这张图总结出:
- 当一个点没有出度时,他就必败
- 当一个点通向的所有点必胜时,他就必败
- 当一个点通向的点中,有一个点必败,他就必胜
可以看到,以上一个点的胜败条件是由他通向的点决定的,所以考虑反向建边。
同时注意,拓扑时一个点的状态如果已经确定就不用再管了。
只有通向他的点中有必胜(已反向),那么他才减入度,直到减到 \(0\) 就判他必败,否则比较难判断是否所有通向他的边都是必胜。
但是只要通向他的点中有必败,就可以直接判必胜了(上文已讲)。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,in[100005],ans[100005],x,y; //1败 2胜
vector<int> a[100005];
queue<int> q;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
a[y].push_back(x),in[x]++;
}
for(int i=1;i<=n;i++){
if(!in[i]) ans[i]=1,q.push(i);
}
while(q.size()){
int k=q.front();q.pop();
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
if(ans[k]==2) in[tmp]--;
if(ans[tmp]!=0) continue;
if(ans[k]==1) ans[tmp]=2,q.push(tmp);
if(!in[tmp]) ans[tmp]=1,q.push(tmp);
}
}
if(ans[1]==1) printf("Sothe\n");
else if(ans[1]==2) printf("Snuke\n");
else printf("Draw\n");
return 0;
}