赛时AC三道,补题做出一道。
A. Mathematical Addition
{% note info no-icon Problem %}
给你两个正整数 \(u,v\),求一对合法的 \(x,y\) 使得 \(\frac{x}{u}+\frac{y}{v}=\frac{x+y}{u+v}\)。
解方程。
\[\begin{array}{c} \frac{vx+uy}{uv}=\frac{x+y}{u+v} \\ (vx+uy)(u+v)=uv(x+y) \\ uvx+u^2y+v^2x+uvy=uvx+uvy \\ u^2y+v^2x=0 \end{array} \]则显然一组合法解为 \(\begin{cases}x=-u^2\\y=v^2\end{cases}\)
B. Coloring Rectangles
{% note info no-icon Problem %}
有一个 \(n\times m\) 的矩阵,每个方格均为红色。你可以任意多次的横切或纵切(必须贯穿整块),不能出现 \(1\times 1\) 的矩阵,问切完后最少需要涂几个蓝色格子才能使得红色格子不相邻。
example: \(2\times 5\)
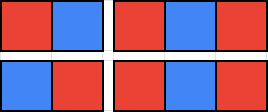
{% endnote %}
{% tabs Solution %}
容易发现,把格子割成 \(1\times 3\) 是最优的,于是考虑在不对后续操作产生影响的前提下,把它切成这样:
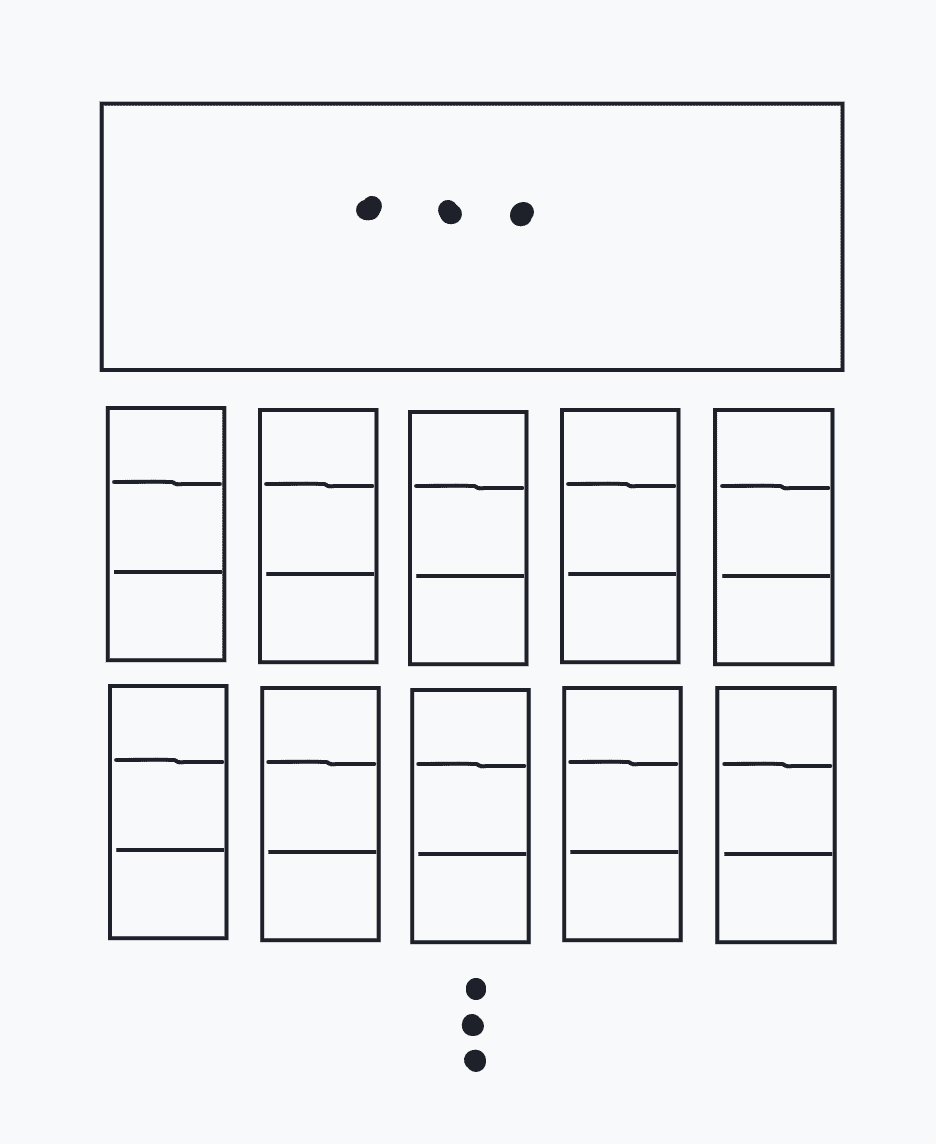
然后再切成这样:
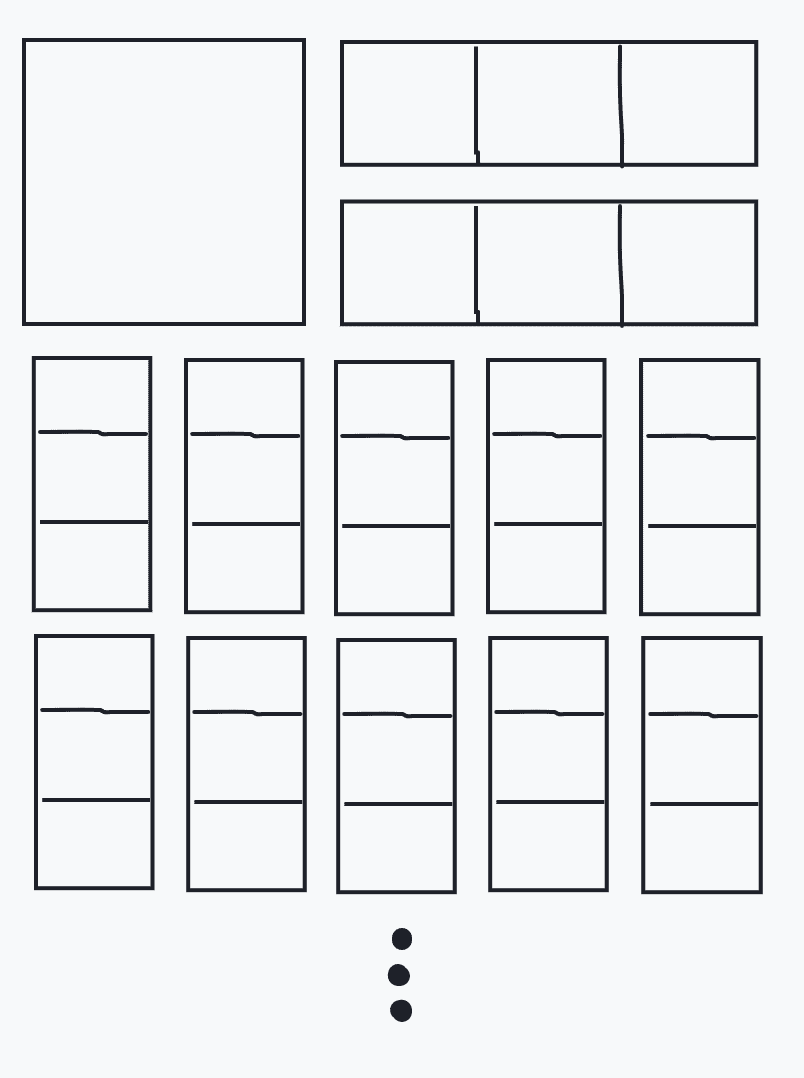
最后特判剩下的。注意切的时候要时刻堤防剩下一行或剩下一列的情况,防止出现 \(1\times 1\)。
通过找规律,我们可以发现,答案为 \(\lceil\frac{n\times m}{3}\rceil\)。
{% endtabs %}
C. Two Arrays
{% note info no-icon Problem %}
给你两个数组 \(a,b\),问能否通过把 \(a\) 进行一次变换得到 \(b\)。
变换方式:在 \(a\) 数组中选出若干个数分别 \(+1\),然后随意排列顺序。
{% endnote %}
大水题。\(a,b\) 分别排序,看是否每个 \(a\) 数组的元素都等于 \(b\) 的对应元素或等于 \(b\) 的对应元素 \(+1\)。
D. Guess the Permutation
{% note info no-icon Problem %}
这是一道交互题。
有一个初始数组 \(a\),满足 \(a_i=i\),即 \({1,2,3...}\)。现在有 \(1<=i<j<=k<=n\),将 \([i,j-1],[j,k]\) 分别翻转。你需要通过不超过 \(40\) 次询问得到 \(i,j,k\) 的值。
每一次询问你可以给出 \(l,r\),得到 \([l,r]\) 中的逆序对个数。
\(n\le 10^9(\log_2(10^9)\approx 30)\)
{% endnote %}
- 用一次 \(\log\) 找到 \(k\):二分 \(mid\),询问 \([mid,r]\) 中逆序对个数,如果不为 \(0\),则 \(k\) 在 \([mid+1,r]\) 中,否则在 \([l,mid]\) 中。
- 用两次询问 \([1,k]\) 和 \([1,k-1]\) 来获得 \(j\) 的位置:一段降序区间 \([l,r]\) 的逆序对数减去 \([l,r-1]\) 的逆序对数等于 \(len-1\),于是 \([1,k]-[1,k-1]=len_{[j,k]}-1\)(\(j\) 前面的都被抵消了),用 \(k-(len-1)\) 即可求出 \(j\)。
- 同理用两次询问 \([1,j-1]\) 和 \([1,j-2]\) 来获得 \(i\) 的位置。
询问次数约为 \(\log(n)+4\)。
不开 long long 见祖宗(逆序对个数最多有 \(n^2\) 级别)。