VP做出来一道,补题又做出来3道。
A. Gamer Hemose
\(Problem\)
你有 \(n\) 个武器,要打一个体力为 \(H\) 的敌人,第 \(i\) 个武器可以对敌人造成 \(a_i\) 的伤害,每把武器不能连续使用两次,问至少需要多少次才能打败敌人。
\(t\le 10^5,\sum n\le 2\times 10^5\)
\(Solution\)
(读错题意调了半天)
肯定是最厉害的武器和次厉害的武器轮番上阵,把它们看作一组,首先算要用多少组,剩余的再单独处理。
时间复杂度 \(O(1)\)。
B. Hemose Shopping
\(Problem\)
你有一个数组,每次操作只能将距离 \(\ge x\) 的两个数交换,问能否排好序。
\(t\le 10^5,\sum n\le 2\times 10^5\)
\(Solution\)
由于每次距离只能 \(\ge x\),中间可能有一段区间是无论如何也动不了的,为 \([n-m+1,m]\)。假设不用考虑这段区间,则剩下的分成左右两边,每次只能交换左右两边的数,是否能排好序呢?能。我们肯定能交换左右两边的数,所以考虑如何交换同一边的数(假设是 \(a_x,a_y\)),我们需要一个在另一边的辅助变量 \(t\),就可以用我们刚学编程是学的用辅助变量来交换变量的方法交换,而 \(t\) 的值也不会改变。
如此,两边的就不用管了,反正总能排好序。接下来考虑中间的部分,因为完全动不了,我们就要求它们已经排好序了。这样就结束了?不。(我就被这个坑了)它们还需要在排好序的数组里处于正确的位置,即,对于排好序的数组 \(b\),\(\forall i\in[n-m+1,m],a_i=b_i\)。
C. Bakry and Partitioning
\(Problem\)
给你一棵有点权的树,问是否能割断至少 \(1\) 条、至多 \(k-1\) 条边,将树分成若干个连通块,使得每个连通块中点权的异或和相等。
\(t\le 5\times 10^4,\sum n\le 2\times 10^5\)
\(Solution\)
如果异或和是 \(0\),随便割一条边即可,因为两边的异或和相等,异或起来的结果才能等于 \(0\)。
如果疑惑和不是 \(0\),而是 \(x\),我们就需要将树分成三个异或和都为 \(x\) 的连通块。为什么不是五个、七个?因为可以合并三个异或和都为 \(x\) 的连通块得到一个异或和为 \(x\) 的连通块。具体实现中跑一边 dfs 即可,跑的过程中一发现出现异或和为 \(x\) 的连通块,马上把它分割出去,统计分割了多少次,如果多于两次就成立,否则不成立。
D. Hemose in ICPC ?
\(Problem\)
这是一道交互题。 给你一棵有边权的树,但你不知道边权是多少,每次你可以询问一个点集,会得到这个点集中距离最远的两个点的距离(即直径)。距离定义为路径中所有边权的 \(\gcd\)。你需要在 \(12\) 次询问以内输出整棵树直径的两个端点。
\(n\le 10^3\)
\(Solution\)
有一个很重要的结论,\(a\ge gcd(a,b)\),这告诉我们树的“直径”一定只有一条边,所以问题转化为我们要求得最长的边的两个端点。我们先花费一次询问得知整棵树的直径(即最长的边),设它为 \(x\)。
假设我们以 \(1\) 号结点为根,那么每一条边唯一对应一个点,所以我们用一个点来代表这个点与它父亲结点之间的边。考虑我们先对所有点按照 dfs 序排序,然后二分选相邻的点集(一定要加上前面的),这样它的直径一定是这个点集中最长的边,如果它是 \(x\),那么递归再这段,否则递归后面的段(也加上前面的)。
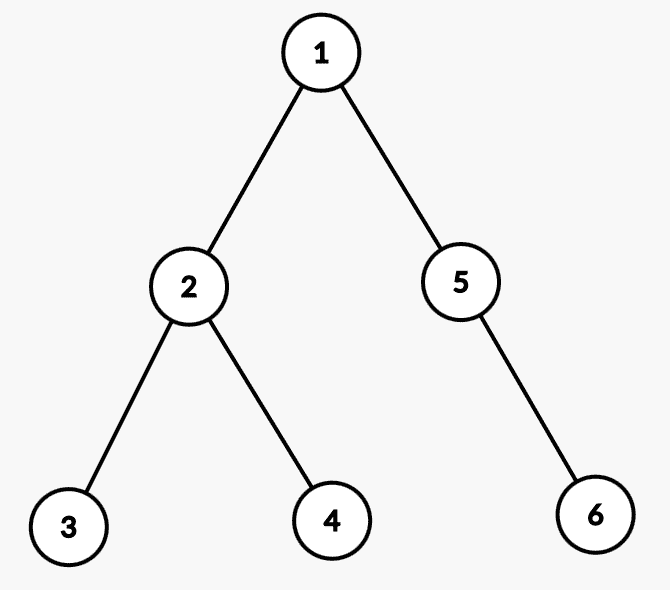
为什么选的点要相邻呢?以下图为例,如果我们问 \({1,3,4}\),它返回 \(10\),我们也不知道是否真的有一条边的权值等于 \(10\),这对我们获知答案没有什么意义。