\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步巩固,难度2颗星!
基础知识
对数函数的概念
函数\(y=log_a x(a>0 ,a ≠1)\)叫做对数函数,其中\(x\)是自变量,定义域是\((0,+∞)\).
解释
函数\(y=log_a x\)中系数为\(1\),底数是不为\(1\)正实数的常数,真数为变量\(x\).
【例】判断下列函数是否为对数函数:
(1) \(y=log_2 x+1\) $\qquad $ (2)\(y=log_3 (x-2)\) \(\qquad\) (3)\(y=3log_5 x\) (4)\(y=log_4 x\)
解析 (1)不是,对数式后加了2;(2)不是,真数不是x;(3)不是,系数不为1;(4)是.
图像与性质
| 函数名称 | 对数函数 | |
| 定义 | 函数$y=log_a x(a>0 ,a ≠1)$叫做对数函数 | |
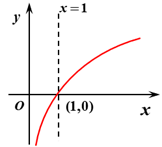
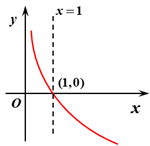
| 图象 | $a>1$ | $0< a <1$ |
 |
 |
|
| 定义域 | $(0,+∞)$ | |
| 值域 | $R$ | |
| 过定点 | 图象过定点$(1 ,0)$ | |
| 奇偶性 | 非奇非偶 | |
| 单调性 | 在$(0 ,+∞)$上是增函数 | 在$(0 ,+∞)$上是减函数 |
| $a$变化对图象的影响 | 在第一象限内,$α$越大图象越靠低; 在第四象限内,$α$越大图象越靠高. | |
可与指数函数就函数的定义域、值域、单调性等函数性质进行比较学习.
【例1】画出函数\(y=log_2 xA\)和 \(y=\log _{\frac{1}{2}} x\)的图象,说下他们的函数性质.
解析

\(y=log_2 x\):定义域是\((0,+∞)\),值域是R,在\((0,+∞)\)上递增,非奇非偶函数;
\(y=\log _{\frac{1}{2}} x\):定义域是\((0,+∞)\),值域是R,在\((0,+∞)\)上递减,非奇非偶函数.
\(y=log_2 x\)与 \(y=\log _{\frac{1}{2}} x\)关于\(x\)轴对称.
【例2】已知图中曲线\(C_1,C_2,C_3,C_4\)分别是函数 \(y=\log _{a_{1}} x\)_, \(y=\log _{a_{2}} x\), \(y=\log _{a_{3}} x\), _\(y=\log _{a_{4}} x\)的图象,则\(a_1,a_2,a_3,a_4\)的大小关系是( )

A.\(a_4<a_3<a_2<a_1\) \(\qquad \qquad\) B.\(a_3<a_4<a_1<a_2\) \(\qquad \qquad\) C.\(a_2<a_1<a_3<a_4\) \(\qquad \qquad\) D.\(a_3<a_4<a_2<a_1\)
解析 由已知图中的四条曲线底数不同及图象的位置关系,再利用\(log_aa=1\)结合图象求解.
对数型函数模型
形如 \(y=k·log_a x(k∈R,\)且\(k≠0;a>0\),且\(a≠1)\)的函数称为对数型函数.
反函数
指数函数\(y=a^x (a>0,\)且\(a≠1)\)与对数函数\(y=log_a x(a>0 ,a ≠1)\)互为反函数.
它们的图象关于直线\(y=x\)对称,定义域与值域相反.
Eg \(y=2^x\)与\(y=log_2x\)互为反函数.

基本方法
【题型1】对数函数的概念
【典题1】 已知对数函数\(f(x)\)的图象经过点 \(\left(\dfrac{1}{9}, 2\right)\),试求\(f(3)\)的值.
解析 设\(f(x)=\log_ax (a>0,\)且\(a≠1)\),
\(∵\)对数函数\(f(x)\)的图象经过点 \(\left(\dfrac{1}{9}, 2\right)\), \(\therefore\left(\dfrac{1}{9}\right)=\log _{a} \dfrac{1}{9}=2\). \(\therefore a^{2}=\dfrac{1}{9}\).
\(\therefore a=\dfrac{1}{3}\), \(\therefore f(x)=\log _{\dfrac{1}{3}} x\).
\(\therefore f(3)=\log _{\dfrac{1}{3}} 3=\log _{\dfrac{1}{3}}\left(\dfrac{1}{3}\right)^{-1}=-1\).
点拨 待定系数法求函数解析式.
巩固练习
1.已知\(f(e^x)=x\),则\(f(5)=\) \(\underline{\quad \quad}\) .
2.函数 \(y=\log _{5}\left(x^{2}-x-2\right)\)的定义域是\(\underline{\quad \quad}\) .
参考答案
-
答案 \(\ln 5\)
解析 令\(t=e^x\),则\(x=\ln t\),所以\(f(t)=\ln t\),即\(f(x)=\ln x\).所以\(f(5)=\ln 5\). -
答案 \(\{x|x>2\)或\(x<-1\}\)
解析 由\(x^2-x-2>0\),解得\(x>2\)或\(x<-1\),
故答案是\(\{x|x>2\)或\(x<-1\}\).
【题型2】对数函数的图象
【典题1】 若函数 \(f(x)=\log _{a}(x+b)\)的图象如图,其中\(a,b\)为常数.则函数\(g(x)=a^x+b\)的大致图象是( )

A. B.
B. C.
C. D.
D.
解析 由函数 \(f(x)=\log _{a}(x+b)\)的图象为减函数可知\(0<a<1\),
\(f(x)=\log _{a}(x+b)\)的图象由\(f(x)=\log_ax\)向左平移可知\(0<b<1\),
故函数\(g(x)=a^x+b\)的大致图象是\(D\),
故选\(D\).
点拨 函数图象的平移变换:左加右减,上加下减.
【典题2】 已知函数\(f(x)=\lg|x-1|\),下列命题中所有正确的序号是\(\underline{\quad \quad}\).
(1)函数\(f(x)\)的定义域和值域均为\(R\);
(2)函数\(f(x)\)在\((-∞,1)\)单调递减,在\((1,+∞)\)单调递增;
(3)函数\(f(x)\)的图象关于\(y\)轴对称;
(4)函数\(f(x+1)\)为偶函数;
(5)若\(f(a)>0\),则\(a<0\)或\(a>2\).
解析 \(∵\)函数\(f(x)=\lg|x-1|\),故有\(x-1≠0\),\(x≠1\),
故定义域为\(\{x|x≠1\}≠R\),故(1)不正确.
由函数\(y=\lg|x-1|\)在\((-∞,1)\)单调递减,在\((1,+∞)\)单调递增,可得
函数\(f(x)=\lg|x-1|\)在\((-∞,1)\)单调递减,在\((1,+∞)\)单调递增,故(2)正确.
由于函数\(f(x)\)的定义域不关于原点对称,故函数\(f(x)\)不具有奇偶性,故(3)不正确.
由于函数\(f(x+1)=\lg|x|\),其图象关于\(y\)轴对称,故是偶函数,故(4)正确.
由\(f(a)>0\),则有\(\lg|a-1|>0\),故\(|a-1|>1\),
\(∴a-1>1\)或\(a-1<-1\),
\(∴a<0\)或\(a>2\),故(5)正确,
故答案为(2)(4)(5).
点拨
函数图象的对称变换
① 函数\(y=f(x)\)\(\stackrel{\text { 图象关于 } y \text { 轴对称 }}{\longrightarrow}\)函数\(y=f(-x)\);
② 函数\(y=f(x)\) \(\stackrel{\text { 图象关于 } x \text { 轴对称 }}{\longrightarrow}\)函数\(y=-f(x)\);
函数图象的翻折变换
① 函数\(y=f(x)\) \(\stackrel{\text { 保留 } x \text { 轴上方图象, } x \text { 轴下方图象关于 } x \text { 轴对称 }}{\longrightarrow}\)函数\(y=|f(x)|\);
② 函数\(y=f(x)\) \(\stackrel{\text { 去掉 } y \text { 轴左边图象, 保留 } y \text { 轴右边图象, 并作 } y \text { 轴对称 }}{\longrightarrow}\)函数\(y=f(|x|)\).
巩固练习
1.已知\(\lg a+\lg b=0\),函数\(f(x)=a^x\)与函数\(g(x)=-\log_bx\)的图象可能是( )
A. B.
B. C.
C. D.
D.
2.函数 \(y=\log _{a}(|x|+1)(a>1)\)的图象大致是( )
A. B.
B. C.
C. D.
D.
3.函数\(y=\lg(|x+1|)\)的大致图象是( )
A. \(\qquad\) B.
\(\qquad\) B. \(\qquad\) C.
\(\qquad\) C. \(\qquad\) D.
\(\qquad\) D.
参考答案
- 答案 \(B\)
解析 \(∵\lg a+\lg b=0\),\(∴ab=1\)则 \(b=\dfrac{1}{a}\)
从而\(g(x)=-\log_bx=\log_ax\),
\(∴\)函数\(f(x)\)与函数\(g(x)\)的单调性是在定义域内同增同减
结合选项可知选\(B\). - 答案 \(B\)
解析 先画\(y=\log_ax (a>1)\),然后将\(y=\log_ax\)的图象向左平移\(1\)个单位得 \(y=\log _{a}(x+1)\),再保留 \(y=\log _{a}(x+1)\)图象在\(y\)轴的右边的图象,\(y\)轴左边的图象与之对称即得到函数 \(y=\log _{a}(|x|+1) \quad(a>1)\)的大致图象.
故选\(B\). - 答案 \(B\)
解析 \(∵\)函数 \(y=\lg (|x+1|)=\left\{\begin{array}{l} \lg (x+1), x>-1 \\ \lg (-x-1), x<-1 \end{array}\right.\),
\(∴\)当\(x>-1\)时,\(y=\lg(x+1)\)的图象是函数\(y=\lg x\)的图象向左平移\(1\)个单位得到的;
当\(x<-1\)时,\(y=\lg(-x-1)\)的图象与函数\(y=\lg(x+1)\)的图象关于直线\(x=-1\)对称,
\(∴\)函数\(y=\lg(|x+1|)\)的大致图象是\(B\).
【题型3】对数函数的应用
角度1 比较指数式的大小
【典题1】 已知 \(a=\dfrac{1}{6} \ln 8, b=\dfrac{1}{2} \ln 5, c=\ln \sqrt{6}-\ln \sqrt{2}\),则 ( )
A.\(a<b<c\) \(\qquad \qquad\) B.\(a<c<b\) \(\qquad \qquad\) C.\(c<a<b\) \(\qquad \qquad\) D.\(c<b<a\)
解析 \(a=\dfrac{1}{6} \ln 8=\dfrac{1}{2} \ln 2\), \(\mathrm{~b}=\dfrac{1}{2} \ln 5\), \(c=\ln \sqrt{6}-\ln \sqrt{2}=\dfrac{1}{2} \ln 3\),
\(∵\ln2<\ln3<\ln5\),\(∴a<c<b\).
故选:\(B\).
点拨 比较对数的大小,主要是利用对数函数的单调性,具体方法有
① 把对数化为同底,利用对数函数的单调性比较大小;
② 若不能化为同底,可对对数进行估值,一般可以与\(0,1\)比较大小;
③ 利用第三个数作为两个数字大小比较的过渡.
角度2 解不等式
【典题1】 设函数 \(f(x)= \begin{cases}2^{1-x}, & x \leq 1 \\ 1-\log _{2} x, & x>1\end{cases}\),则满足\(f(x)≤2\)的\(x\)的取值范围是( )
A.\([-1,2]\) \(\qquad \qquad\) B.\([0,2]\) \(\qquad \qquad\) C.\([1,+∞)\) \(\qquad \qquad\) D.\([0,+∞)\)
解析 由 \(f(x) \leq 2 \Leftrightarrow\left\{\begin{array}{l}
2^{1-x} \leq 2 \\
x \leq 1
\end{array}\right.\)或 \(\left\{\begin{array}{l}
x>1 \\
1-\log _{2} x \leq 2
\end{array} \Leftrightarrow x \geq 0\right.\),
\(∴\)满足\(f(x)≤2\)的\(x\)的取值范围是\([0,+∞)\),
故选\(D\).
点拨 利用对数函数的单调性求解不等式,同时要注意函数的定义域.
角度3 值域
【典题1】 已知\(f(x)=2+\log_3x\),\(x∈[1,3]\),求 \(y=[f(x)]^{2}+f\left(x^{2}\right)\)的最大值及相应的\(x\).
解析 \(∵f(x)=2+\log_3x\),\(x∈[1,3]\),
\(\therefore y=[f(x)]^{2}+f\left(x^{2}\right)=\left(\log _{3} x\right)^{2}+6 \log _{3} x+6\)且定义域为\([1,3]\).
令\(t=\log_3x (x∈[1,3])\).
\(∵t=\log_3x\)在区间\([1,3]\)上是增函数,\(∴0≤t≤1\).
从而要求 \(y=[f(x)]^{2}+f\left(x^{2}\right)\)在区间\([1,3]\)上的最大值,
只需求\(y=t^2+6t+6\)在区间\([0,1]\)上的最大值即可.
\(∵y=t^2+6t+6\)在\([-3,+∞)\)上是增函数,
\(∴\)当\(t=1\),即\(x=3\)时, \(y_{\max }=1+6+6=13\).
综上可知,当\(x=3\)时, \(y=[f(x)]^{2}+f\left(x^{2}\right)\)的最大值为\(13\).
巩固练习
1.比较下列各组中两个值的大小.
(1)\(\log_31.9\),\(\log_32\);\(\qquad \qquad\) (2)\(\log_23\),\(\log_{0.3}2\);
2.解下列不等式 \(\log _{\frac{1}{7}} x>\log _{\frac{1}{7}}(4-x)\);
3.若关于\(x\)的方程 \(\log _{\frac{1}{2}} x=\dfrac{m}{m-1}\)在区间\((0,1)\)上有解,则实数\(m\)的取值范围是\(\underline{\quad \quad}\) .
4.求下列函数的值域:
(1) \(y=\log _{2}\left(x^{2}+4\right)\); \(\qquad \qquad\) (2) \(y=\log _{\frac{1}{2}}\left(3+2 x-x^{2}\right)\).
参考答案
-
答案 (1)\(\log_31.9<\log_32\) (2)\(\log_23>\log_{0.3}2\)
解析 (1)因为函数\(y=\log_3x\)在\((0,+∞)\)上是增函数,
所以\(f(1.9)<f(2)\).所以\(\log_31.9<\log_32\).
(2)因为\(\log_23>\log_21=0\),\(\log_{0.3}2<\log_{0.3}1=0\),
所以 \(log_23>\log_{0.3}2\). -
答案 \(\{x|0<x<2\}\)
解析 由已知,得 \(\left\{\begin{array}{l} x>0 \\ 4-x>0 \\ x<4-x \end{array}\right.\),解得\(0<x<2\).
所以原不等式的解集是\(\{x|0<x<2\}\). -
答案 \((-∞,0)∪(1,+∞)\)
解析 当\(x∈(0,1)\)时, \(\log _{\frac{1}{2}} x \in(0,+\infty)\),
所以要使方程 \(\log _{\frac{1}{2}} x=\dfrac{m}{m-1}\)在区间\((0,1)\)上有解,只需 \(\dfrac{m}{m-1}>0\)即可,
解得\(m<0\)或\(m>1\),所以实数\(m\)的取值范围是\((-∞,0)∪(1,+∞)\). -
答案 (1) \([2,+∞)\) (2) \([-2,+∞)\)
解析 (1)\(∵x^2+4≥4\), \(\therefore y=\log _{2}\left(x^{2}+4\right) \geq \log _{2} 4=2\).
\(∴\)函数 \(y=\log _{2}\left(x^{2}+4\right)\)的值域为\([2,+∞)\).
(2)设\(u=3+2x-x^2\),则\(u=-(x-1)^2+4≤4\).\(∵u>0\),\(∴0<u≤4\).
又 \(y=\log _{\frac{1}{2}} u\)在\((0,+∞)\)上为减函数, \(\therefore \log _{\frac{1}{2}} u \geq-2\).
\(∴\)函数 \(y=\log _{\frac{1}{2}}\left(3+2 x-x^{2}\right)\)的值域为\([-2,+∞)\).
【题型4】综合解答题
【典题1】 已知函数 \(f(x)=\left(\log _{2} x-2\right)\left(\log _{4} x-\dfrac{1}{2}\right)\)
(1)当\(x∈[2,4]\)时,求该函数的值域;
(2)若\(f(x)≥m\log_2 x\)对于\(x∈[4,16]\)恒成立,求\(m\)的取值范围.
解析 (1) \(f(x)=\left(2 \log _{4} x-2\right)\left(\log _{4} x-\dfrac{1}{2}\right)\)
令\(t=\log_4 x,x∈[2,4]\)时, \(t \in\left[\dfrac{1}{2}, 1\right]\),
此时, \(y=(2 t-2)\left(t-\dfrac{1}{2}\right)=2 t^{2}-3 t+1=2\left(t-\dfrac{3}{4}\right)^{2}-\dfrac{1}{8}\),
\(\because t \in\left[\dfrac{1}{2}, 1\right]\), \(\therefore y \in\left[-\dfrac{1}{8}, 0\right]\),
所以函数的值域为 \(\left[-\dfrac{1}{8}, 0\right]\);
(2) \(f(x)≥m\log_2x\)对于\(x∈[4,16]\)恒成立,
即\(2t^2-3t+1≥mt\)对\(t∈[1,2]\)恒成立,
\(\therefore m \leq 2 t+\dfrac{1}{t}-3\)对\(t∈[1,2]\)恒成立,
易知 \(g(t)=2 t+\dfrac{1}{t}-3\)在\(t∈[1,2]\)上单调递增,
\(\therefore g(t)_{\min }=g(1)=0\),
\(∴m≤0\).
点拨
1.注意到\(\log_4 x\)与\(\log_2x\)的关系,采取换元法求函数值域;
2.恒成立问题利用分离参数法把问题转化为最值问题求参数范围.
巩固练习
1.已知函数\(f(x)=\lg(1+2x)\),\(F(x)=f(x)-f(-x)\).
(1)求函数\(F(x)\)的定义域;
(2)当 \(0 \leq x<\dfrac{1}{2}\)时,总有\(F(x)≥m\)成立,求\(m\)的取值范围.
2.已知函数 \(f(x)=\left|\log _{2}(x+1)\right|\),实数\(m、n\)在其定义域内,且\(m<n\),\(f(m)=f(n)\).
求证:(1)\(m+n>0\);(2) \(f\left(m^{2}\right)<f(m+n)<f\left(n^{2}\right)\).
参考答案
- 答案 (1) \(\left(-\dfrac{1}{2}, \dfrac{1}{2}\right)\) (2)\(m≤0\)
解析 (1)由题意可知:\(F(x)=\lg(1+2x)-\lg(1-2x)\),
\(∴1+2x>0\)且\(1-2x>0\),即 \(-\dfrac{1}{2}<x<\dfrac{1}{2}\),
所以函数\(F(x)\)的定义域是 \(\left(-\dfrac{1}{2}, \dfrac{1}{2}\right)\);
(2)由题意可知\(F(x)=\lg \dfrac{1+2 x}{1-2 x}\),
设 \(u(x)=\dfrac{1+2 x}{1-2 x}\),则有 \(u(x)=-1+\dfrac{2}{1-2 x}\);
当 \(0 \leq x<\dfrac{1}{2}\)时有:\(0≤2x<1\),即\(-1<-2x≤0\),
则有\(0<1-2x≤1\),则 \(\dfrac{1}{1-2 x} \geq 1\),
故而 \(\dfrac{2}{1-2 x} \geq 2\), \(-1+\dfrac{2}{1-2 x} \geq 1\);
\(\therefore u(x)_{\min }=1\)_, _\(F(x)_{\min }=\lg 1=0\);
又由题意可得: \(m \leq F(x)_{\min }\),
\(∴m≤0\). - 解析 (1)证明:由\(f(m)=f(n)\),得 \(\left|\log _{2}(m+1)\right|=\left|\log _{2}(n+1)\right|\),
即\(\log_2(m+1)=±\log_2(n+1)\),
\(\log_2(m+1)=\log_2(n+1)\),① 或\(\log _{2}(m+1)=\log _{2} \dfrac{1}{n+1}\).②
由①得\(m+1=n+1\),与\(m<n\)矛盾,舍去.
由②得 \(m+1=\dfrac{1}{n+1}\),即\((m+1)(n+1)=1\).③
\(∴m+1<1<n+1\).\(∴m<0<n\).\(∴mn<0\).
由③得\(mn+m+n=0\),\(m+n=-mn>0\).
(2)证明:当\(x>0\)时, \(f(x)=\left|\log _{2}(x+1)\right|=\log _{2}(x+1)\)在\((0,+∞)\)上为增函数.
由(1)知 \(m^2-(m+n)=m^2+mn=m(m+n)\),且\(m<0\),\(m+n>0\),
\(∴m(m+n)<0\).
\(∴m^2-(m+n)<0\),\(0<m^2<m+n\).
\(∴f(m^2)<f(m+n)\).
同理, \((m+n)-n^2=-mn-n^2=-n(m+n)<0\),
\(∴0<m+n<n^2\),\(∴f(m+n)<f(n^2)\).
\(∴f(m^2 )<f(m+n)<f(n^2 )\).
分层练习
【A组---基础题】
1.函数 \(y=\left(\dfrac{1}{3}\right)^{x}\)与函数 \(f(x)=\log _{\frac{1}{2}} x\)的图象的交点的个数为( )
A. \(0\) \(\qquad \qquad\) B.\(1\) \(\qquad \qquad\) C.\(2\)\(\qquad \qquad\) D.\(3\)
2.函数\(y=\lg|x|\) ( )
A.是偶函数,在区间\((-∞,0)\)上单调递增
B.是偶函数,在区间\((-∞,0)\)上单调递减
C.是奇函数,在区间\((-∞,0)\)上单调递增
D.是奇函数,在区间\((-∞,0)\)上单调递减
3.设\(a=6^0.4\),\(b=\log_{0.4}0.5\),\(c=\log_80.4\),则\(a,b,c\)的大小关系是( )
A.\(a<b<c\) \(\qquad \qquad\) B.\(c<b<a\) \(\qquad \qquad\) C.\(c<a<b\) \(\qquad \qquad\) D.\(b<c<a\)
4.函数 \(y=\log _{\frac{1}{2}}\left(x^{2}-6 x+17\right )\)的值域是( )
A.\(R\) \(\qquad \qquad\) B.\([8,+∞)\) \(\qquad \qquad\) C.\((-∞,-3]\) \(\qquad \qquad\) D.\([3,+∞)\)
5.已知 \(f(x)=\left\{\begin{array}{l}
(6-a) x-4 a, x<1 \\
\log _{a} x, x \geq 1
\end{array}\right.\)在区间\((-∞,+∞)\)上是单调递增函数,则实数\(a\)的取值范围是( )
A.\((1,6)\) \(\qquad \qquad\) B. \(\left[\dfrac{6}{5}, 6\right)\) \(\qquad \qquad\) C. \(\left[1, \dfrac{6}{5}\right]\) \(\qquad \qquad\) D.\((1,+∞)\)
6.不等式\(\log_2x<1\)的解是\(\underline{\quad \quad}\).
7.设函数 \(f(x)=\left\{\begin{array}{l}
\ln x, x>e \\
a-x^{2}, x \leq e
\end{array}\right.\),若函数\(f(x)\)的值域为\(R\),则实数\(a\)的取值范围是\(\underline{\quad \quad}\).
8.已知函数\(f(x)=|\ln x|\),若\(f(m)=f(n)(m>n>0)\),则 \(\dfrac{m}{m+1}+\dfrac{n}{n+1}=\)\(\underline{\quad \quad}\).
9.关于函数 \(f(x)=\lg \dfrac{x^{2}+1}{|x|}\)有下列说法:
(1)函数\(y=f(x)\)的图象关于\(y\)轴对称;
(2)函数\(f(x)\)的最小值是\(\lg2\);
(3)当\(x>0\)时,\(f(x)\)是增函数,当\(x<0\)时,\(f(x)\)是减函数;
(4)\(f(x)\)在区间\([-1,0),[1,+∞)\)上是增函数;
(5)\(f(x)\)无最大值,也无最小值.
其中正确的命题序号是\(\underline{\quad \quad}\).
10.已知函数 \(f(x)=\lg \dfrac{x^{2}+1}{-x}\)且 \(a≠1)\).
(1)求函数\(f(x)\)的定义域;
(2)判断函数\(f(x)\)的奇偶性;
(3)求使\(f(x)>0\)的\(x\)的取值范围.
参考答案
-
答案 \(B\)
解析 分别画出函数 \(y=\left(\dfrac{1}{3}\right)^{x}\)(红色曲线)与函数 \(f(x)=\log _{\dfrac{1}{2}} x\)(蓝色曲线)的图象,如图所示

由图象可知,函数 \(y=\left(\dfrac{1}{3}\right)^{x}\)与函数 \(f(x)=\log _{\dfrac{1}{2}} x\)的图象的交点的个数有\(1\)个,
故选:\(B\). -
答案 \(B\)
解析 函数\(y=\lg|x|\)定义域为\(\{x|x≠0\}\),而\(\lg|-x|=\lg|x|\),所以该函数为偶函数,
\(y=\lg x\)在\((0,+∞)\)上单调递增,
\(∴\)函数\(y=\lg|x|\)在\((-∞,0)\)上单调递减,在\((0,+∞)\)上单调递增;故选\(B\). -
答案 \(B\)
解析 \(∵a=6^0.4>1\),\(b=\log_{0.4} 0.5∈(0,1)\),\(c=\log_8 0.4<0\),\(∴a>b>c\).故选:\(B\). -
答案 \(C\)
解析 \(∵t=x^2-6x+17=(x-3)^2+8≥8\)
\(∴\)内层函数的值域变\([8,+∞)\), 而 \(y=\log _{\frac{1}{2}} t\)在\([8,+∞)\)是减函数,故 \([8,+∞)\)
\(∴\)函数 \(y \leq \log _{\frac{1}{2}} 8=-3\)的值域是\((-∞,-3]\), 故应选\(C\). -
答案 \(B\)
解析 \(f(x)\)在\((-∞,+∞)\)上为单调递增函数;
\(\therefore\left\{\begin{array}{l} 6-a>0 \\ a>1 \\ (6-a) \cdot 1-4 a \leq \log _{a} 1 \end{array}\right.\);解得 \(\dfrac{6}{5} \leq a<6\);
\(∴\)实数\(a\)的取值范围为 \(\left[\dfrac{6}{5}, 6\right)\).故选:\(B\). -
答案 \(\{x|0<x<2\}\)
解析 不等式\(\log_2x<1\),即不等式\(\log_2 2<\log_2 2\),\(∴0<x<2\), -
答案 \([1,+∞)\)
解析 \(x>e\)时,\(f(x)>1\),\(x≤e\)时,\(f(x)=a-x^2≤a\),
\(∵\)函数\(f(x)\)的值域为\(R\),\(∴a≥1\),
\(∴\)实数\(a\)的取值范围是\([1,+∞)\). -
答案 \(1\)
解析 由题意,函数\(f(x)=|\ln x|\),
\(∵f(m)=f(n)\),\(∴|\ln m|=|\ln n|\)
\(∵m>n>0\),\(∴-\ln m=\ln n\),即\(\ln m+\ln n=0\),可得\(nm=1\),
则 \(\dfrac{m}{m+1}+\dfrac{n}{n+1}=\dfrac{2 m n+m+n}{n m+n+m+1}=\dfrac{2+m+n}{1+m+n+1}=1\). -
答案 (1),(2),(4)
解析 \(∵\)函数 \(f(x)=\lg \dfrac{x^{2}+1}{|x|}(x \neq 0), \quad f(-x)=\lg \dfrac{x^{2}+1}{|x|}=f(x)\),
故函数为偶函数,其图象关于\(y\)轴对称;故(1)正确;
当\(x=±1\)时,函数取最小值\(\lg2\),无最大值,故(2)正确,(5)错误;
当\(x>0\)时, \(f(x)=\lg \dfrac{x^{2}+1}{x}\),在\((0,1]\)上为减函数,在\([1,+∞)\)上是增函数;
当\(x<0\)时, \([-1,0)\),在\((-∞,-1]\)上为减函数,在\([-1,0)\)上是增函数;
故(3)错误,(4)正确;
故答案为:(1),(2),(4). -
答案 (1) \((-1,1)\) (2) 奇函数 (3) 当\(a>1\)时,\(0<x<1\);当\(0<a<1\)时,\(-1<x<0\).
解析 (1)由 \(\dfrac{1+x}{1-x}>0\),得\(-1<x<1\),故函数\(f(x)\)的定义域为\((-1,1)\).
(2) \(\because f(-x)=\log _{a} \dfrac{1-x}{1+x}=-\log _{a} \dfrac{1+x}{1-x}=-f(x)\),
又由(1)知函数\(f(x)\)的定义域关于原点对称,
\(∴\)函数\(f(x)\)是奇函数.
(3)当\(a>1\)时,由 \(\log _{a} \dfrac{1+x}{1-x}>0=\log _{a} 1\),得 \(\dfrac{1+x}{1-x}>1\),解得\(0<x<1\);
当\(0<a<1\)时,
由 \(\log _{a} \dfrac{1+x}{1-x}>0=\log _{a} 1\),得 \(0<1-\dfrac{1+x}{1-x}<1\),解得\(-1<x<0\).
故当\(a>1\)时,\(x\)的取值范围是\(\{x|0<x<1\}\);
当\(0<a<1\)时,x的取值范围是\(\{x|-1<x<0\}\).
【B组---提高题】
1.设\(a>0\),\(b>0\),则下列叙述正确的是( )
A.若\(\ln a-2b>\ln b-2a\),则\(a>b\)
B.若\(\ln a-2b>\ln b-2a\),则\(a<b\)
C.若\(\ln a-2a>\ln b-2b\),则\(a>b\)
D.若\(\ln a-2a>\ln b-2b\),则\(a<b\)
2.已知\(x=\log_3 2\),\(y=\ln 2\),\(z=2^{-1}\),则( )
A.\(x<y<z\) \(\qquad \qquad\) B.\(z<y<x\) \(\qquad \qquad\) C.\(z<x<y\) \(\qquad \qquad\) D.\(y<z<x\)
3.设\(f(x)=|\ln (x+1)|\),已知\(f(a)=f(b)(a<b)\),则( )
A.\(a+b>0\) \(\qquad \qquad\) B.\(a+b>1\) \(\qquad \qquad\) C.\(2a+b>0\) \(\qquad \qquad\) D.\(2a+b>1\)
4.已知函数 \(f(x)=\left|\log _{2}(x-1)\right|, g(x)=\left(\dfrac{1}{2}\right)^{x}\),则图象交于\(A(x_1,y_1)\),\(B(x_2,y_2)\)两点,则( )
A.\(x_1\cdot x_2<1\) \(\qquad \qquad\) B.\(x_1+x_2>5\)\(\qquad \qquad\) C.\(x_1+x_2>x_1\cdot x_2\) \(\qquad \qquad\) D.\(x_1+x_2<x_1\cdot x_2\)
5.关于函数 \(y=\log _{2}\left(x^{2}-2 x+3\right)\)有以下\(4\)个结论:
①该函数是偶函数; \(\qquad \qquad\) ②定义域为\((-∞,-3]∪(1,+∞)\);
③递增区间为\([1,+∞)\); \(\qquad \qquad\) ④最小值为\(1\);
其中正确结论的序号是\(\underline{\quad \quad}\).
6.若\(x_1\)满足\(2^x=5-x\),\(x_2\)满足\(x+\log_2x=5\),则\(x_1+x_2\)等于\(\underline{\quad \quad}\) .
7.已知函数 \(f(x)=\left(\log _{4} x-3\right) \cdot \log _{4}(4 x)\).
(1)当 \(x \in\left[\dfrac{1}{4}, 16\right]\)时,求该函数的值域;
(2)令 \(g(x)=f(x)+\log _{4} x^{2}-2 a \cdot \log _{4} x\),求\(g(x)\)在 \(x \in\left[4^{2}, 4^{4}\right]\)的最值.
8.设函数\(f(x)=|\log_ax |(a>0,a≠1)\),实数\(t<4\),关于\(x\)的方程\(f(x)=t^2\)的根为\(x_1,x_2 (x_1<x_2)\),关于\(x\)的方程\(f(x)=8-2t\)的根为\(x_3,x_4 (x_3<x_4)\),记\(A=|x_1-x_3 |,B=|x_2-x_4 |\).
(1)当 \(a=\dfrac{1}{2}, t=1\)时,求\(B\)的值;
(2)若\(a>1\),且当\(t\)变化时,记 \(g(t)=\dfrac{A}{B}\).
①求函数\(g(t)\)的表达式; ②求函数\(g(t)\)的最大值.
参考答案
-
答案 \(A\)
解析 \(∵y=\ln x\)与\(y=2x\)均为增函数,
故\(f(x)=\ln x+2x\)在\((0,+∞)\)上为增函数,
故\(f(a)>f(b)⇔a>b>0\),
即\(\ln a+2a>\ln b+2b⇔a>b>0\),
即\(\ln a-2b>\ln b-2a⇔a>b>0\),
故选:\(A\). -
答案 \(C\)
解析 \(\log _{3} 2=\dfrac{1}{\log _{2} 3}, \ln 2=\dfrac{1}{\log _{2} e}, 2^{-1}=\dfrac{1}{2}\);
又\(2>\log_2 3>\log_2 e>1\); \(\therefore \dfrac{1}{2}<\dfrac{1}{\log _{2} 3}<\dfrac{1}{\log _{2} e}\);
\(∴z<x<y\).故选:\(C\). -
答案 \(A\)
解析 易知\(y=\ln (x+1)\)在定义域上是增函数,而\(f(x)=|\ln (x+1)|\),且\(f(a)=f(b)\);
故\(-\ln (a+1)=\ln (b+1)\),即\(ab+a+b=0\).
\(0=a b+a+b<\dfrac{(a+b)^{2}}{4}+a+b\),即\((a+b)(a+b+4)>0\),
显然\(-1<a<0\),\(b>0\),
\(∴a+b+4>0\),\(∴a+b>0\),故选:\(A\). -
答案 \(C\)
解析不妨设\(x_1<x_2\),
作出\(f(x)\)和\(g(x)\)的图象,由图象知\(x_1<2,x_2>2\),
则 \(f\left(x_{1}\right)=\left|\log _{2}\left(x_{1}-1\right)\right|=-\log _{2}\left(x_{1}-1\right), f\left(x_{2}\right)\)\(=\left|\log _{2}\left(x_{2}-1\right)\right|=\log _{2}\left(x_{2}-1\right)\),
则\(f(x_2 )-f(x_1 )=\log_2(x_2-1)+\log_2(x_1-1)\)
\(=\log _{2}\left(x_{1}-1\right)\left(x_{2}-1\right)=\left(\dfrac{1}{2}\right)^{x_{2}}-\left(\dfrac{1}{2}\right)^{x_{1}}<0\),
即\((x_1-1)(x_2-1)<1\),即\(x_1 x_2-(x_1+x_2)+1<1\),即\(x_1+x_2>x_1\cdot x_2\),
故选:\(C\).

-
答案 ③④
解析 函数 \(y=\log _{2}\left(x^{2}-2 x+3\right)\)的定义域为\(R\),故②错误;
\(f(-x)=\log _{2}\left(x^{2}+2 x+3\right) \neq f(x)\),故\(f(x)\)不是偶函数,故①错误;
令\(t=x^2-2x+3\),则\(y=\log_2t\),
由\(t=x^2-2x+3\)的单调递增区间为\([1,+∞)\);
\(y=\log_2t\)为增函数,故函数 \(y=\log _{2}\left(x^{2}-2 x+3\right)\)的递增区间为\([1,+∞)\),故③正确;
当\(x=1\)时函数取最小值为\(1\),故④正确;
故正确结论的序号是:③④.
故答案为:③④ -
答案 \(5\)
解析 由题意\(x_1+2^x1=5\)①,\(x_2+\log_2 x_2=5\) ②,
所以\(5-x_1=2^{x_1}\),故有\(5-x_2=\log_2 x_2\).
故\(x_1\)和\(x_2\)是直线\(y=5-x\)和曲线\(y=2^x\)、曲线\(y=\log_2x\)交点的横坐标.
再根据函数\(y=2^x\)和函数\(y=\log_2x\)互为反函数,它们的图象关于直线\(y=x\)对称,
故曲线\(y=2^x\)和函数\(y=\log_2x\)的图象交点关于直线\(y=x\)对称.
即点\((x_1,5-x_1 )\)和点\((x_2,5-x_2 )\)构成的线段的中点在直线\(y=x\)上,
即 \(\dfrac{x_{1}+x_{2}}{2}=\dfrac{5-x_{1}+5-x_{2}}{2}\),求得\(x_1+x_2=5\), -
答案 (1) \([-4,0]\)
(2) ①当\(a≤2\)时, \(y_{\min }=f(2)=1-4 a\); \(y_{\max }=f(4)=13-8 a\);
②当\(2<a≤3\)时, \(y_{\min }=f(a)=-a^{2}-3\); \(y_{\max }=f(4)=13-8 a\);
③当\(3<a<4\)时,\(y_{\min }=f(a)=-a^{2}-3\);\(y_{\max }=f(2)=1-4 a\)
④当\(a≥4\)时, \(y_{\min }=f(4)=13-8 a\); \(y_{\max }=f(2)=1-4 a\).
解析 (1)函数 \(f(x)=\left(\log _{4} x-3\right) \cdot \log _{4} 4 x=\left(\log _{4} x\right)^{2}-2 \log _{4} x-3\),
令\(t=\log_4x\), \(\chi \in\left[\dfrac{1}{4}, 16\right] \Rightarrow t \in[-1,2]\),
此时有\(y=t^2-2t-3\),对称轴\(t=1∈[-1,2]\),
当\(t=1\)时,取得最小值 \(-4\);\(t=-1\)函数取得最大值 \(0\).
\(∴y∈[-4,0]\).
(2) \(g(x)=f(x)+\log _{4} x^{2}-2 a \cdot \log _{4} x=\left(\log _{4} x\right)^{2}-2 \log _{4} x-3\),
令\(t=\log_4x\), \(x \in\left[4^{2}, 4^{4}\right]\),则\(t∈[2,4]\),
此时有\(f(t)=t^2-2at-3\),
①当\(a≤2\)时, \(y_{\min }=f(2)=1-4 a\); \(y_{\max }=f(4)=13-8 a\);
②当\(2<a≤3\)时, \(y_{\min }=f(a)=-a^{2}-3\); \(y_{\max }=f(4)=13-8 a\);
③当\(3<a<4\)时,\(y_{\min }=f(a)=-a^{2}-3\);\(y_{\max }=f(2)=1-4 a\)
④当\(a≥4\)时, \(y_{\min }=f(4)=13-8 a\); \(y_{\max }=f(2)=1-4 a\). -
答案 (1) \(62\) (2)① \(g(t)=a^{-(t-1)^{2}-7}(t \in(-\infty,-4) \cup(-4,2) \cup(2,4))\)② \(a^{-7}\)
解析 (1)当 \(a=\dfrac{1}{2}, t=1\)时,由\(f(x)=t^2\),得 \(\left|\log _{\frac{1}{2}} x\right|=1\), \(\log _{\frac{1}{2}} x=-1\)或 \(\log _{\frac{1}{2}} x=1\),
由题意得 \(x_{1}=\dfrac{1}{2}, x_{2}=2\)
由\(f(x)=8-2t\),得 \(\left|\log _{\dfrac{1}{2}} x\right|=6\), \(\therefore \log _{\frac{1}{2}} x=-6\)或 \(\log _{\dfrac{1}{2}} x=6\),
由题意得 \(x_{3}=\dfrac{1}{64}, x_{4}=64\),
则\(B=|x_2-x_4 |=62\)
(2)若\(a>1\),由\(f(x)=t^2\),得\(|\log_ax |=t^2\),则 \(\log _{a} x=-t^{2}\)或\(\log_ax=t^2\),
则\(x_{1}=a^{-t^{2}}, \quad x_{2}=a^{t^{2}}\),
由\(f(x)=8-2t\),得 \(|\log_ax |=8-2t\), \(\therefore \log _{a} x=2 t-8\)或\(\log_ax=8-2t\).
则 \(x_{3}=a^{2 t-8}, x_{4}=a^{8-2 t}\),
则 \(A=\left|x_{1}-x_{3}\right|=\left|a^{-t^{2}}-a^{2 t-8}\right|, B=\left|a^{t^{2}}-a^{8-2 t}\right|\)
① \(g(t)=\dfrac{A}{B}=\dfrac{\left|a^{-t^{2}}-a^{2 t-8}\right|}{\left|a^{t^{2}-a^{8-2 t}}\right|}=a^{-\left(t^{2}-2 t+8\right)}=a^{-(t-1)^{2}-7}\),
使函数\(g(t)\)有意义,则必须满足\(t^2≠8-2t\),即\(t≠-4\)且\(t≠2\),
又\(t<4\),所以函数\(g(t)\)的定义域为\((-∞,-4)∪(-4,2)∪(2,4)\);
②当\(t=1\)时,\(g(t)\)取得最大值,最大值为 \(a^{-7}\) .
【C组---拓展题】
1.已知函数\(f(x)\)是\(R\)上的奇函数,且满足\(f(x+2)=-f(x)\),当\(x∈(0,1]\)时,\(f(x)=2^x-1\),则方程 \(f(x)=\log _{7}|x-2|\)解的个数是( )
A.\(8\) \(\qquad \qquad\) B.\(7\) \(\qquad \qquad\) C.\(6\) \(\qquad \qquad\) D.\(5\)
2.已知\(x_1\)是方程\(10^x=-x-2\)的解,\(x_2\)是方程\(\lg x=-x-2\)的解,函数\(f(x)=(x-x_1)(x-x_2)\),则( )
A.\(f(0)<f(2)<f(3)\) \(\qquad \qquad\) B.\(f(2)=f(0)<f(3)\) \(\qquad \qquad\) C.\(f(3)<f(0)=f(2)\) \(\qquad \qquad\) D.\(f(0)<f(3)<f(2)\)
3.已知\(x,y,z>0\),且 \(\text { 1. } 2^{x}=3^{y}=5^{z}\),试比较 \(\dfrac{1}{2 x^{\prime}}, \dfrac{1}{3 y^{\prime}}, \dfrac{1}{5 z}\)的大小.
参考答案
-
答案 \(B\)
解析 函数\(f(x)\)是\(R\)上的奇函数,\(f(0)=0\),
由\(f(x+2)=-f(x)\),可得\(f(x+4)=f(x)\),\(∴f(x)\)的周期\(T=4\).
作出在同一坐标系中画\(y=2^x-1\)和 \(y=\log _{7}|x-2|\)图象,
从图象不难看出,其交点个数\(7\)个,
故选:\(B\). -
答案 \(A\)
解析 设直线\(l\)的方程为:\(y=-x-2\),设\(l\)与\(y=10^x\),\(y=\lg x\)分别相交于\(A,B\)两点,
\(∵y=10^x\)与\(y=\lg x\)互为反函数,
\(∴\)它们的图象关于直线\(y=x\)对称,
由题意得:点\(A(x_1,-x_1-2)\)与点\(B(x_2,-x_2-2)\)关于直线\(y=x\)对称,
\(∴AB\)的中点在直线\(y=x\)上,
\(\therefore \dfrac{-x_{1}-2-x_{2}-2}{2}=\dfrac{x_{1}+x_{2}}{2}\),即\(-x_1-2-x_2-2=x_1+x_2\),
\(∴x_1+x_2=-2\),
\(∴f(x)=(x-x_1 )(x-x_2 )=x^2-(x_1+x_2 )x+x_1 x_2\)\(=x^2+2x+x_1 x_2\),
其对称轴方程为:\(x=-1\),
\(∴f(x)\)在\([-1,+∞)\)上单调递增,
\(∴f(0)<f(2)<f(3)\),故选:\(A\). -
答案 \(\dfrac{1}{5 z}<\dfrac{1}{2 x}<\dfrac{1}{3 y}\)
解析 设\(2x=3y=5z=k\),\((k>1)\),则\(x=\log_2k\),\(y=\log_3k\),\(z=\log_5k\),
\(\therefore \dfrac{1}{2 x}=\dfrac{1}{2 \log _{2} k}=\dfrac{1}{2} \log _{k} 2=\log _{k} \sqrt{2}\)_, _\(\dfrac{1}{3 y}=\dfrac{1}{3 \log _{3} k}=\dfrac{1}{3} \log _{k} 3=\log _{k} \sqrt[3]{3}\),
\(\dfrac{1}{5 z}=\dfrac{1}{5 \log _{5} k}=\dfrac{1}{5} \log _{k} 5=\log _{k} \sqrt[5]{5}\),
\(\because(\sqrt{2})^{6}=8,(\sqrt[3]{3})^{6}=9\), \(\therefore \sqrt{2}<\sqrt[3]{3}\)
\(\because(\sqrt{2})^{10}=2^{5}=32\),\((\sqrt[5]{5})^{10}=5^{2}=25\)
\(\therefore \sqrt{2}>\sqrt[5]{5}\)
\(\therefore \sqrt[5]{5}<\sqrt{2}<\sqrt[3]{3}\),即 \(\dfrac{1}{5 z}<\dfrac{1}{2 x}<\dfrac{1}{3 y}\).