前置知识:最大权闭合子图。
这是个什么东东呢,它是对于每一个点赋一个值,求一个点集,点集内的所有点都必须包含它的所有后继,使这个点集的和最大。
如以下图:
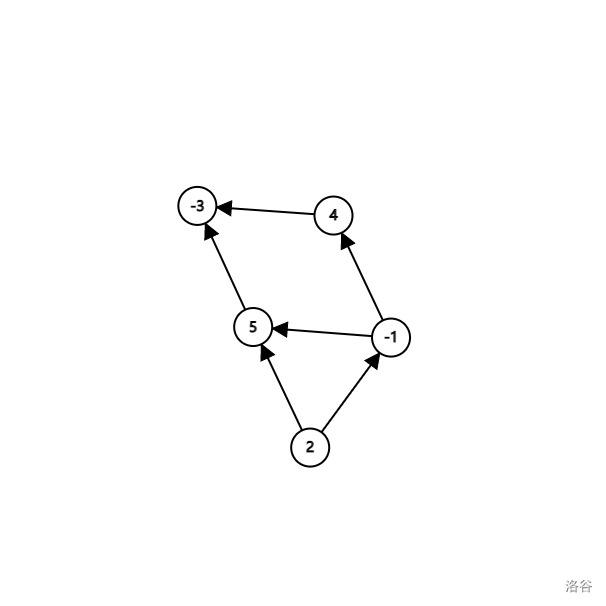
图中的编号代表点权。
可以知道的是,能选择的点集有:\(\left\{-3\right\},\left\{-3,4\right\},\left\{-3,5\right\},\left\{-3,4,5\right\},\left\{-3,4,5,-1\right\},\left\{-3,4,5,-1,2\right\},\emptyset\)。
最大的明显为 \(\left\{-3,4,5,-1,2\right\}\),为 \(-3+4+5-1+2=7\)。
这种类型的题我们如何解决呢,首先对于点权为负的,我们对其于汇点建边,而为正的点则用源点与其建边,其他边不变,原来图上的边设为正无穷,而新建的边为点权的绝对值。

没有设边权的代表边权无限大。
那么我们在这上面跑一次最小割,然后用所有从源点出发的边权和减去最小割即可,如图中,边权和为 \(11\),最小割为 \(4\),那么答案即为 \(7\)。
考虑证明:
首先割掉一条源点上的边代表你不会选择这个点,而割掉连向汇点上的一条边代表你会选择这个点。
很好说明,因为在割去汇点上的边时,代表你要选这个点,且正点也用流量与负点进行了抵消。
如果图不联通,那么选的点集一定合法,因为如果联通,说明你选择了正点,而正点有负点后继没有进行选择。
所以综上所言,我们就可以用最小割求出这个问题了。
那么如何证明这是最优解呢。
我们知道:最小割为:\(\text{不选的正权}+\text{要选的负权的绝对值}\)。
而答案为:\(\text{正权和}-\text{不选的正权和}+\text{选择的负权和}\),后面那个即是最小割,由于最小割保证了最小,所以答案也就最大。
那么这个最大权闭合子图有什么用呢,那就先看到我们这道题:CF311E Biologist。
这题一下貌似没什么思路,先进行分析。
首先我们假设所有点初始为 \(1\),那么所有的 \(1\) 的询问我们都是满足的。
现在我们想满足一些 \(0\) 的询问,那么对于本来是 \(0\) 的点,等同于我们需要把点权加回来,而本来是 \(1\) 的点,则要扣去其费用。
对于本来是 \(0\) 的询问,满足以后要加回本应有的钱,如果要倒扣也要加回来。
而对于本来是 \(1\) 的询问,由于点变为 \(0\) 导致无法满足,所以将其全部扣除应得的钱。
那么可以把加操作看成点权为正,源点与其相连,而减操作看成点权为负,与汇点相连。
那么这次的最后答案是什么呢。
首先最小割为:\(\text{没加上的点}+\text{减去的点的绝对值}\)。
而由于我们假使所有数为 \(1\),所以答案为 \(1\) 询问减去修改 \(0->1\) 再减去 \(0\) 的倒扣钱。而这次与源点连接的所有边权和为 \(0\) 询问加上修改 \(0->1\) 加上 \(0\) 的倒扣钱。
两者加起来即为所有询问的价值,即 \(\sum W_i\)。
最终答案即为 \(\sum W_i-\text{最小割}\)。
总结一下总过程:
1、对原来为 \(0\) 的点,用源点与其建边,边权为其改变状态的价值。
2、对原来为 \(1\) 的边,对汇点建边,边权为其改变状态的价值。
3、对于每一个 \(0\) 询问,单独重新创一个点,用源点与其相连,边权为其钱数,如果要倒扣,边权加上倒扣的钱即可,然后用这个新点对询问的点建边,边权为无限(即如果选这个询问它的后继都要选择改变状态)。
4、对于每一个 \(1\) 询问,单独创一个点,对汇点建边,边权为其钱数,如果要倒扣,边权加上倒扣的钱即可,然后用询问的点对这个新点建边,边权为无限(即如果要选择一个连向新点的点,那就要扣除这个点)。
建了边后跑最小割即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int N=1e6+5;
const int M=2e6+5;
int n,m,g,h[M],p[N],s,t,st[N],cnt,vis[N],dep[N];
struct node
{
int to,data,next;
}a[M];
inline void addedge(int x,int y,int k)
{
a[cnt]={y,k,h[x]};
h[x]=cnt++;
a[cnt]={x,0,h[y]};
h[y]=cnt++;
}
queue<int>q;
bool bfs()
{
//cout<<'b';
for(int i=1;i<=n+m+2;i++)dep[i]=0;
q.push(s);
dep[s]=1;
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=h[x];i!=-1;i=a[i].next)
{
if(a[i].data==0)continue;
if(!dep[a[i].to])
{
dep[a[i].to]=dep[x]+1;
q.push(a[i].to);
}
}
}
return dep[t];
}
int dfs(int x=s,int num=1e9)
{
if(x==t)return num;
if(vis[x])return 0;
for(int i=h[x];i!=-1;i=a[i].next)
{
if(a[i].data==0)continue;
if(dep[a[i].to]==dep[x]+1)
{
vis[x]=1;
int sum=dfs(a[i].to,min(num,a[i].data));
if(sum)
{
a[i].data-=sum;
a[i^1].data+=sum;
return sum;
}
}
}
return 0;
}
int main()
{
memset(h,-1,sizeof(h));
scanf("%d%d%d",&n,&m,&g);
s=n+m+1;
t=n+m+2;
for(int i=1;i<=n;i++)scanf("%d",&p[i]);
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
if(p[i]==0)addedge(s,i,x);
else addedge(i,t,x);
}
int ans=0;
for(int i=1;i<=m;i++)
{
int opt,w,k,ss;
scanf("%d%d%d",&opt,&w,&k);
ans+=w;
for(int j=1;j<=k;j++)scanf("%d",&st[j]);
scanf("%d",&ss);
for(int j=1;j<=k;j++)
{
if(opt==0)addedge(i+n,st[j],w+ss*g);
else addedge(st[j],i+n,w+ss*g);
}
if(opt==0)addedge(s,i+n,w+ss*g);
else addedge(i+n,t,w+ss*g);
}
while(bfs())
{
memset(vis,0,sizeof(vis));
int num=dfs();
while(num)
{
ans-=num;
memset(vis,0,sizeof(vis));
num=dfs();
}
}
printf("%d",ans);
return 0;
}