2023-02-20

1.1线性方程组

1.线性方程组

1.方程组 -> rearrange(重排,化简) ->未知量在同侧的等式

eg. :x₁ - 3 + x₂ = 3x₁ + 2x₂(未化简) ----> -2x₁ - x₂ = -3(已化简)

2.方程组的解:

一个数列sn分别代替方程中xn,则称s_n组成的集合为方程组的解集

1.一个方程组可能有解,可能无解,可能有无限个解,有解的情况下,有且只有一组解

有解,则称方程组"相容"(consistent)

无解,则称方程组"不相容"(inconsistent)

3.方程组的矩阵形式

1.方程组的系数矩阵:矩阵中包含未知量的系数,排序顺序每一列应保持为同一未知量的系数,每一行按顺序排

2.方程组的系数增广矩阵(简称增广矩阵):在系数矩阵的基础上,在行末加上该行方程等号右侧的常数

方程组与其矩阵一一对应

4.矩阵：矩形数据阵列

1.m行n列的矩阵表述为m*n(可以简化方程组写法)

2.矩阵的三种初等变换：

1.行间交换

2.单行乘以非零常数

3.一行乘以非零常数加上另一行

3.一次或多次初等行变换可逆，因此可知:两个矩阵可以通过有限步初等行变换，则两个矩阵行等价
两个方程组增广矩阵行等价=方程组等价

1.2矩阵的行化减和阶梯形

1.阶梯形：

1.定义与要求:

1.每一个非零行在零行之上；

2.每一行第一个非零数值（先导元素）位于前一行的右边；

3.某一个先导元素所在列下方元素都是0

图例1,一个阶梯型矩阵示意图

2.简化阶梯形：

先导元素必须是1，先导元素列都要满足除1以外都是0（简化阶梯形唯一）

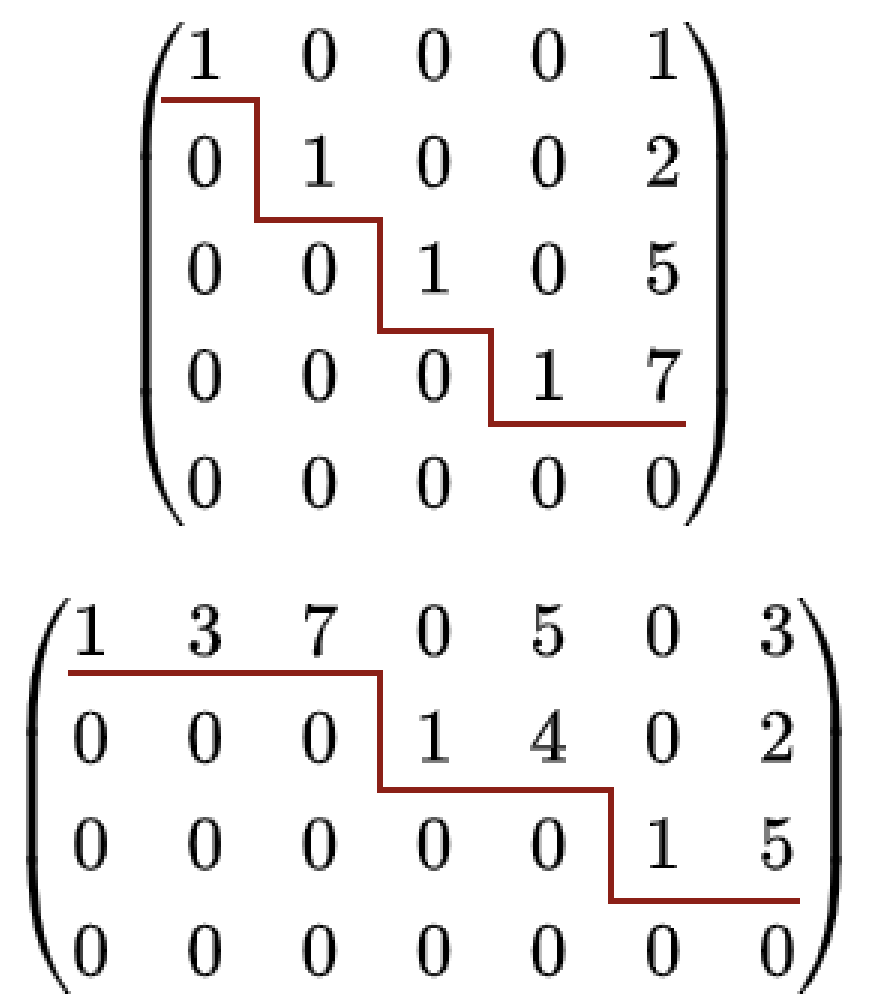
图例2,图为两个简化阶梯型,其中上图容易看出是简化阶梯型,下图第一眼容易看错

2.主元：

1.定义:

先导元素所在的位置成为主元位，在主元位的元素叫做主元，主元所在的列叫主元列

2.将普通矩阵计算为阶梯型矩阵的步骤：

1.先选主元（先导元素位置）
2.把主元下的元素消为0
3.得到新矩阵
4.重复步骤直至得到阶梯形