标签：implies gcd 数论 varphi pmod delta equiv

数论笔记

求\(\varphi(n)\)

普通求法：

首先将n唯一分解为$n=x_1^{p_1}*x_2……*x_n^{p_n} $

\(\varphi(n)=n*(1-\frac1{x_1})*(1-\frac1{x_2})*……*(1-\frac1{x_n})\)

证明：

首先我们考虑在所有数中有\(\frac{1}{x}\)的概率会取到一个数是x的倍数，那么有\((1-\frac{1}{x})\)的概率会取到一个数不是x的倍数，1-n有n个数，我们要找到1-n所有与n互质的数，也就是去一个不是n的任意一个因数(x1,x2,x3……xn)的倍数，就得到以上式子

线性求\(\varphi(1)\)到\(\varphi(n)\)的所有

首先我们先明白两个定理：

\[1.\begin{cases} \varphi(nm)=\varphi(n)*\varphi(m)~~~~~gcd(n,m)=1\\ \varphi(nm)=\varphi(n)*m~~~~~~~~~~~gcd(n,m)=m \end{cases} \]

在\(gcd(n,m)=1\)条件下

定理1证明：
根据上述式子可以推导：
$n=x_1^{p_1}*x_2……x_n^{p_n} \( \)m=y_1^{q_1}*y_2……y_n^{q_n} \( \)nm=x_1^{p_1}*x_2……x_n^{p_n}*y_1*y_2^{{q_2}……*y_n} $

\(\varphi(nm)=n*m*(1-\frac1{x_1})……*(1-\frac1{x_n})*(1-\frac1{y_1})……*(1-\frac1{y_n})=\varphi(n)*\varphi(m)~~~~~~~~~~~~gcd(n,m)=m\)

2.\(\varphi(n)=n-1~~~~~~~~~~~~~n\in prim\)

考虑感性理解，1-n里面有\(\varphi(n)\)个与n互质，那么扩大m倍，相当于有m个1-n就直接乘(因为我们保证了\(gcd(n,m)=m\)也就是n是m的倍数,所以不存在乘上m后多出了不属于n的因子)

因此，我们可以来用质数筛的方法求\(\varphi()\)

void op(int n){
    for(int i=2;i<=n;i++){
        if(!vis[i]){
            prim[++tot]=i;
            phi[i]=i-1;//引用定理2
        }
        for(int j=1;j<=tot&&i*prim[j]<=n;j++){
            vis[prim[j]*i]=1;
            if(i%prim[j]==0){
                phi[i*prim[j]]=phi[i]*prim[j];
                break;
            }else{
                phi[i*prim[j]]=phi[i]*(prim[j]-1);//因为prim[j]是质数，所以i与prim[j]一定互质
            }
        }
    }
}

EXCRT

给你一些方程：

\[x\equiv a_1\pmod {p_1}\\ x\equiv a_2\pmod {p_2}\\ ......\\ x\equiv a_n\pmod {p_n} \]

普通CRT比较有限制(因为要保证p为质数)

那么接下来我们来学习

扩展中国剩余定理

首先我们考虑将这些方程两两合并：

先转化一下

\[x\equiv a_1\pmod {p_1}\implies x=k_1p_1+a_1\\ x\equiv a_2\pmod {p_2}\implies x=k_2p_2+a_2 \]

上减下

\(k1p1-k1p1+a1-a2=0\implies k1p1-k2p2=a2-a1\)

已知\(p1,p2,a1,a2\) 这就是一个二元一次不定方程啊，直接exgcd

先算\(d=gcd(p_1,p_2)\)

判断\(d|(a2-a1)\) 如果不成立，则直接无解

\(\implies \frac {k_1} d p1- \frac {k_2} d p2=\frac {a2-a1} d\)

我们转换成exgcd的形式方便计算：

\[k1p1-k2p2=a2-a1 \implies x_0a+y_0b=gcd(a,b);~~~~~~~~~~(a=p_1,b=p_2)\\ \frac {a_2-a_1} {a_2-a_1}*gcd(a,b)=gcd(a,b)\\ \frac {k_1} {a_2-a_1} *gcd(a,b)=x_0\implies{k_1}=\frac {x_0} {gcd(a,b)}*(a_2-a_1)\\ \frac {k_2} {a_2-a_1} *gcd(a,b)=y_0\implies{k_2}=\frac {y_0} {gcd(a,b)}*(a_2-a_1)\\ \]

算出\(k_1~k_2\)就可以得到一个解满足\(k1p1-k2p2=a2-a1\)

这个解也就满足\(x'=k_1p_1+a_1=k_2p_2+a_2\)

我们找到了一个特殊解\(x'\)满足

\[x\equiv a_1\pmod {p_1}\implies x=k_1p_1+a_1\\ x\equiv a_2\pmod {p_2}\implies x=k_2p_2+a_2 \]

那么通解是什么捏？

通解\(x=x'+k*lcm(p_1,p_2)\)

因此我们由得到了一个方程：

\(x=x'+k*lcm(p_1,p_2)\implies x\equiv x'\pmod {lcm(p_1,p_2)}\)

我们成功的合并了两个式子！

把所有的都合并就好啦AWA

拓展欧拉定理

欧拉定理:

\(a^{\varphi(m)} \equiv1\pmod m~~~~~~~~~~~~~~~~~~~~(gcd(a,m)=1)\)

拓展欧拉定理：

\[a^b\equiv a^{b~mod~\varphi(m)+\varphi(m)}\pmod m~~~~~~~~~~~~~~(b>\varphi(m)) \]

这里没有a,m互质的要求

证明

首先我们唯一分解\(m=p_1^{q_1}p_2^{q_2}......p_n^{q_n}\)

现在我们只需要证明对于每个\(p_i^{q_i}都有\)

\(a^b\equiv a^{b~mod~\varphi(m)+\varphi(m)}\pmod {p_1^{q_1}}\)

因为

\[\left. \begin{matrix} x\equiv y\pmod {m_1}\\ x\equiv y\pmod {m_2}\\ \end{matrix} \right\} \implies x\equiv y\pmod{m1m2} \]

(x-y既是m1倍数也是m2倍数)

如果\(gcd(a,{p_i^{q_i}})=1\)

\[a^b\equiv a^{\lfloor \frac b {\varphi(m)}\rfloor*\varphi(m)+b~mod~\varphi(m)}\equiv a^{b~mod~\varphi(m)}\pmod {p_i^{q_i}} \]

因为

\[\varphi(x)=\varphi(p_1)*p_1^{q_1-1}*\varphi(p_2)*p_2^{q_2-1}*......\varphi(p_n)*p_n^{q_n-1}\\ \varphi(p_i^{q_i})=\varphi(p_i)*p_i^{q_i-1}\\ a^{\varphi(p_i^{q_i})}\equiv 1 \pmod {p_i^{q_i}} \]

总的来说：

\[\lfloor \frac b {\varphi(m)}\rfloor*\varphi(m)=k*\varphi({p_i^{q_i}}) \]

证毕

如果\(gcd(a,p_i^{q_i})\ne 1\)

因为\(p_i\)为质数，所以一定有\(p_i|a\)

因为\(b\ge\varphi(m)\ge\varphi(p_i^{q_i})\ge{q_i}\)

\[\left. \begin{matrix} a^b\equiv0\pmod {p_i^{q_i}}\\ a^{\varphi(m)}\equiv0 \pmod{p_i^{q_i}} \end{matrix} \right\} \implies a^b\equiv a^{{\varphi(m)}}\pmod {{p_i}^{q_i}} \]

综上所述

\[\begin{cases} a^b\equiv a^{b~mod~\varphi(m)}\pmod {p_i^{q_i}}~~~~~~~~gcd(a,p_i)=1\\ a^b\equiv a^{{\varphi(m)}}\pmod {{p_i}^{q_i}}~~~~~~~~~~~~~~~gcd(a,p_i)\ne1 \end{cases} \]

如何合并？

\[\implies\begin{cases} a^b\equiv a^{\varphi(m)+b~mod~\varphi(m)}\pmod {p_i^{q_i}}~~~~~~~~~~~~gcd(a,p_i)=1\\ a^b\equiv a^{\varphi(m)+b~mod~\varphi(m)}\pmod {{p_i}^{q_i}}~~~~~~~~~~~gcd(a,p_i)\ne1\ \end{cases} \]

第一个式子，乘上一个\(\varphi(m)\)欧拉定理结果不变

第二个式子\(a^{\varphi(m)}\equiv0\pmod {p_i^{q_i}}\)随便乘上一些东西没什么关系

综上：

\[a^b\equiv a^{\varphi(m)+b~mod~\varphi(m)}\pmod {m} \]

BSGS

有这样一个方程

\[a^x\equiv b\pmod m~~~~~~~~~~~~~~~~~~gcd(a,m)=1 \]

已知a,b,m。求x

根据群论的知识，在\(x\in[1,m]\implies b\in[1,m]\)

我们枚举 \(x\) ，可以得到答案，但时间复杂度不能接受

我们考虑更优秀的枚举：

\(设x=A\times\sqrt m-B(A,B\in[1,{\sqrt m}])\)

可以发现现在依旧 \(x\in[1,m]\)

转换一下

\[a^{A\times\sqrt m-B}\equiv b\pmod m\implies a^{A\times\sqrt m}\equiv b\times a^B\pmod m \]

发现现在只有两个未知数A,B我们可以先枚举一次B预处理

用map记录所有\(b \times a^B~ mod~m\)

再枚举A算出\(a^{A*\sqrt m}~mod~m\)在map找找有没有对应的

原根

1.定义

a模p的次数（阶）是在\(a^e\equiv1\pmod p\)的最小指数e

符号语言:\(\delta_p(a)\)代表a在mod p的意义下的最小指数e使\(a^e\equiv1\pmod p\)

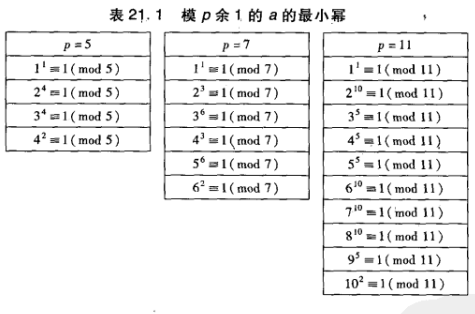
我们进行观察可以发现：

定理1.\(\delta_p(a)|\varphi(p)\)

一定是这样的，我们来证明一下：

已知~~\(a^{\delta_q(a)}\equiv1\pmod p\\\)
设n使得\(a^n\equiv1\pmod p\\\)
设\(G=gcd(\delta_q(a),n)\\\)
一定存在(u,v)使得\(\delta_q(a)u-nv=G\)(由exgcd可得)

\[\begin{cases} a^{\delta_p(a)u}=(a^{\delta_p(a)})^u\equiv1^u\equiv1\pmod p\\ a^{\delta_p(a)u}=a^{nv+G}=(a^n)^v*a^G\equiv1*a^G\equiv a^G\pmod p \end{cases} \implies a^G\equiv1\pmod p \]

因为\(e_p(a)\)是同余于1(mod p)最小次幂，所以\(G\ge \delta_p(a)\)

而设\(G=gcd(\delta_q(a),n)\),所以\(G\le \delta_p(a)\)

综上\(G=\delta_p(a)\implies \delta_p(a)|n\implies\delta_p(a)|\varphi(p)\)

定理2.

\[\delta_p(ab)=\delta_p(a)\delta_p(b) \iff gcd(\delta_p(a),\delta_p(b))=1 \]

证明：必要性。

\[ab^{lcm(\delta(a),\delta(b))}\equiv1\pmod p\implies \delta_p(ab)|lcm(\delta_p(a),\delta_p(b))\\ \implies\delta_p(a)\delta_p(b)|lcm(\delta_p(a),\delta_p(b))\implies gcd(\delta_p(a),\delta_p(b))=1 \]

证明：充分性

\[ab^{\delta_p(ab)}\equiv ab^{\delta_p(ab)\delta(b)}\equiv a^{\delta_p(ab)\delta(b)} (b^{\delta_p(b)})^{\delta_p(ab)} \equiv a^{\delta_p(ab)\delta(b)}\equiv1\pmod p\\ \implies\delta_p(a)|{\delta_p(ab)\delta(b)}\\ \because \begin{cases} \delta_p(a)|{\delta_p(ab)\delta(b)}\\ gcd(a,b)=1 \end{cases} \implies \delta(a)|\delta(ab) \]

同理

\[\begin{cases} \delta(a)|\delta(ab)\\ \delta(b)|\delta(ab)\\ gcd(a,b)=1 \end{cases} \implies \delta(a)\delta(b)|\delta(ab) \]

还有

\[(ab)^{\delta(a)\delta(b)}\equiv (a^{\delta(a)})^{\delta(b)}*(b^{\delta(b)})^{\delta(a)} \equiv 1\pmod p\\ \implies\delta(ab)|\delta(a)\delta(b) \]

得出

\[\delta(ab)=\delta(a)\delta(b) \]

上面一堆东西屁用没有

下面我们来求原根：

原根定义：

\[a^{q}\not\equiv 1\pmod m~~~~~~~~~q,a\in[1,\varphi(m))\cup Z \]

满足上述则a是模m意义下的原根

如何找出最小的原根g呢？

我们从1开始枚举now，如果\(gcd(now,n)\ne1\)那一定不是原根

找出一个可能是原根的数，我们从\([1-\varphi(n))\)枚举每个k判断\(now^k\equiv1\pmod m\)是否成立

如果全都不同余1，那么就找到了g，可以容易的找出其他原根：

    while(++g){
        int now=1,bj=0;
        if(gcd(g,n)!=1) continue;
        for(int j=1;j<phi[n];j++){
            now=now*g%n;
            if(now==1){
                bj=1;
                break;
            }
        }
        if(bj==1) continue;
        else if(bj==0){
            break;
        }
    }

如何找出其他原根

我们认为g是最小的原根

寻找方法：

\[在gcd(k,\varphi(m))条件下,(g^{k})也是模m意义下的原根 \]

先学习定理3

然后我们来证明这样的寻找方法是正确的

\[\delta_m(g)=\varphi(m)\\ \delta_m(g^k)=\frac {\varphi(m)} {gcd(\varphi(m),k)} \]

我们要使得\(\frac {\varphi(m)} {gcd(\varphi(m),k)}=\varphi(m)\)

所以\(gcd(\varphi(m),k)=1\)

代码

    int now=g;
    ans[++cnt]=g;
    for(int j=2;j<phi[n];j++){
        now=now*g%n;
        if(gcd(j,phi[n])!=1) continue;
        ans[++cnt]=now;
    }

如何知道模m意义下有无原根呢？

这些数有原根

\(结论：2,4,p^k,2×p^k，其中 p 为奇素数，k 为正整数。\)

证明详见

原根

如何知道原根数量

我们在前面可以知道，当求出一个g(最小原根)，

\[在gcd(k,\varphi(m))=1条件下,(g^{k})也是模m意义下的原根~~~k\in[1,\varphi(m)) \]

有多少个k满足:\(k\in[1,\varphi(m))~~~gcd(k,\varphi(m))=1\)

其实就是\(\varphi(\varphi(m))\)

总代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int phi[N],prim[N],v[N],vis[N],tot=0,ans[N],cnt=0;
int t,n,d;
void pre(){
    phi[1]=1;
    for(int i=2;i<=N-1;i++){
        if(!v[i]){
            prim[++tot]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=tot&&prim[j]*i<=N-10;j++){
            v[i*prim[j]]=1;
            if(i%prim[j]==0){
                phi[i*prim[j]]=phi[i]*prim[j];
                break;    
            }else{
                phi[i*prim[j]]=phi[i]*phi[prim[j]];
            } 
        }
    }
    vis[2]=1;
    vis[4]=1;
    for(int i=2;i<=tot;i++){
        for(long long j=1;j<=N;j=j*prim[i]){
            if(j>N-10){
                break;    
            }
            vis[j]=1;
            if(2*j<=N-1) vis[2*j]=1;
        }
    }
}//预处理phi和prime
int gcd(int x,int y){
    if(y==0) return x;
    return gcd(y,x%y);
}
void input(){
    scanf("%d",&t);
    for(int i=1;i<=t;i++){
        cnt=0;
        memset(ans,0,sizeof(ans));
        scanf("%d%d",&n,&d);
        if(!vis[n]){
            printf("0\n\n");
            continue;    
        }
        int g=0;
        while(++g){
            int now=1,bj=0;
            if(gcd(g,n)!=1) continue;
            for(int j=1;j<phi[n];j++){
                now=now*g%n;
                if(now==1){
                    bj=1;
                    break;
                }
            }
            if(bj==1) continue;
            else if(bj==0){
                break;
            }
        }
        int now=g;
        ans[++cnt]=g;
        for(int j=2;j<phi[n];j++){
            now=now*g%n;
            if(gcd(j,phi[n])!=1) continue;
            ans[++cnt]=now;
        }
        sort(ans+1,ans+1+cnt);
        printf("%d\n",phi[phi[n]]);
        for(int j=1;j<=phi[phi[n]]/d;j++){
            printf("%d ",ans[j*d]);
        }
        printf("\n");

    }
}
int main(){
//     freopen("1.txt","w",stdout);
    pre();
    input();

    return 0;
}

完结撒花~~~~

标签：implies,gcd,数论,varphi,pmod,delta,equiv
From： https://www.cnblogs.com/hfjh/p/17132559.html