论 2023 深圳市适应性考试的一道错题

回顾一下问题：

给定 \(c_1,c_2\)，要求 \(\{ A | A \in c_1, \exist B \in c_2 \ \text{s.t.} \ \text{dis}(A,B) \leq 8\}\)。

我们事实上找到了 \(f: c_2 \mapsto c_1\) 满足 \(f(B) = A, \text{dis}(A,B) = \min_{A'\in c_1}\{\text{dis}(A', B)\}\)。

官方解答事实上只算入了 \(\{f(B) | B \in c_2, \text{dis}(B, f(B)) \leq 8\}\)。

但是，这真的是对的吗？

你会发现对于某个 \(A \in c_1\)，可能存在一个 \(B \in c_2\) 使得 \(\text{dis}(A,B) \leq 8\) 但 \(f(B) \neq A\)。此时这个 \(A\) 可能不会被算入。

好了，所以你知道它有问题了。

几何直观：

以双曲线为圆心 \(8\) 为半径作圆，则这个圆内扫到直线的部分，则是合法的点集。

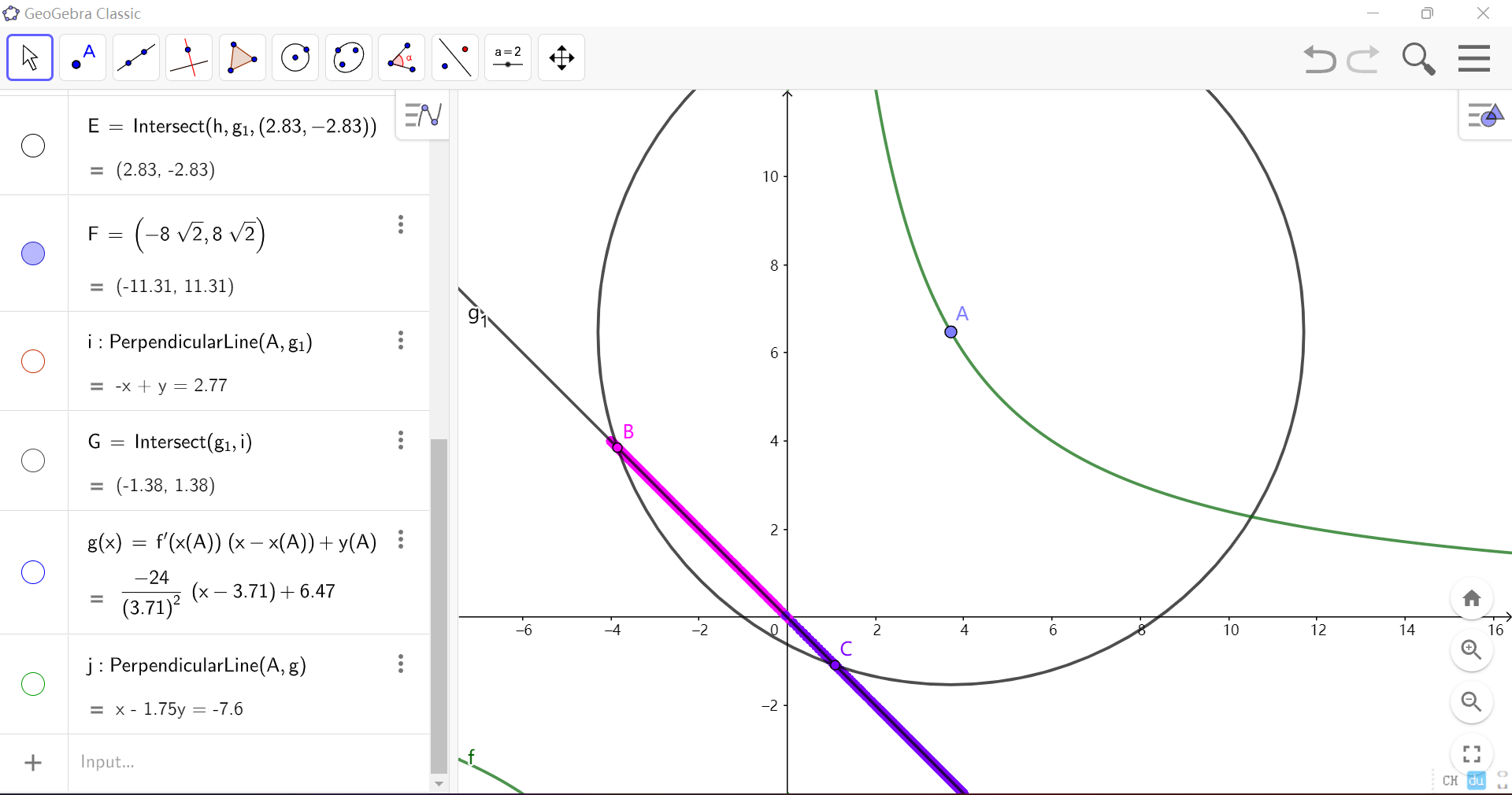
这里只画出了边缘的点，有色的一段即为合法的。

再把标答算法的结果输出来。

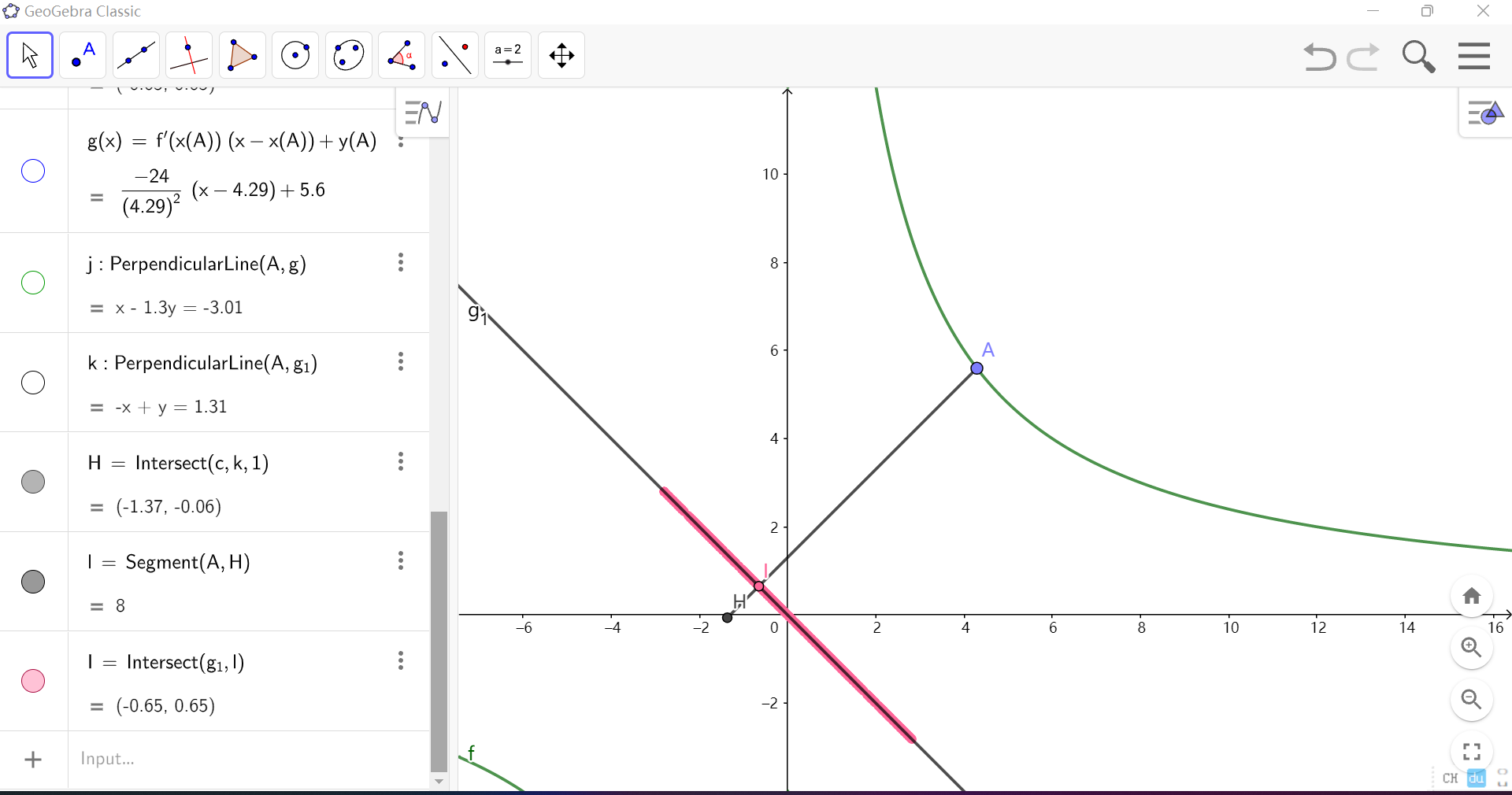
若与 \(A\) 最近的直线上的点距离小于等于 \(8\) 则标记为合法。

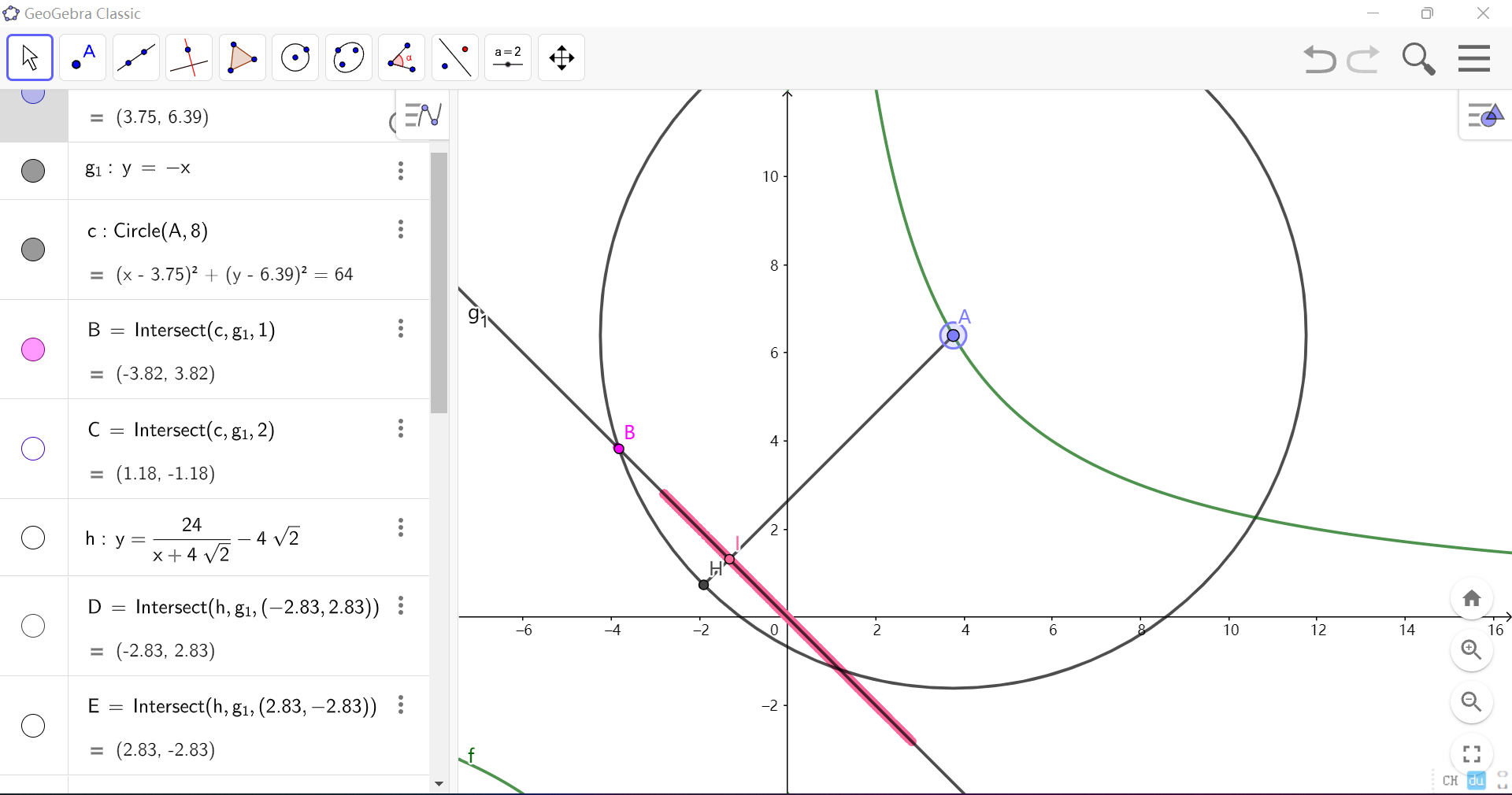
它不对了。

手动画一下会发现 \(I\) 上移到一个位置后 \(B\) 随之下移最后同时到达粉色段的边缘。这就是为什么官方答案只考虑了粉色段。

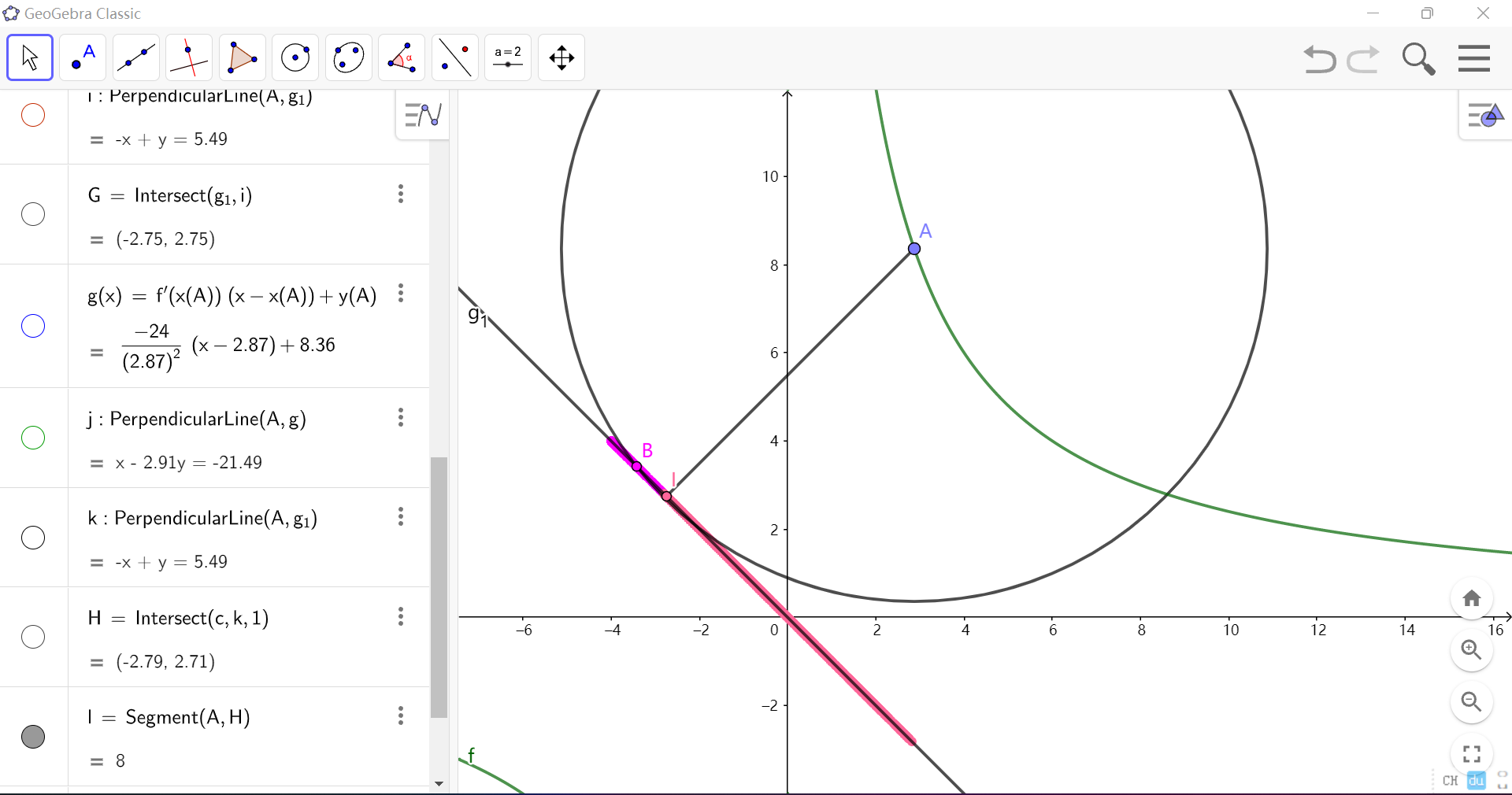
答案是 \(80 \sqrt{2}\)，有同学有证明了。等会补。