RSA常见题型------2023.2.17

标签：gmpy2 17 题目 RSA 2023.2 flag import print 加密

1，已知dp,dq求解m

其中关系式如下:

dp=d%(p-1)
dq=d%(q-1)

解题脚本：

#!/usr/bin/python  
#coding:utf-8  
  
import gmpy2  
from Crypto.Util.number import long_to_bytes  
  
c = xxx  
p = xxx  
q = xxx  
dp = xxx  
dq = xxx   
  
InvQ=gmpy2.invert(q,p)  
mp=pow(c,dp,p)  
mq=pow(c,dq,q)  
m=(((mp-mq)*InvQ)%p)*q+mq  
  
print long_to_bytes(m) 

2，e=2把密文c开平方求解

在RSA加密中，由于e只有2，相当于把明文m平方了而已，得到的c也比n小很多。尝试把c开根号看能否得到明文。Python自带的开根号求解的数并不打。我们可以使用gmpy2库来对大整数开根号。

题目: 01-西湖论剑rsa

已知:
e=2
c=9217979941366220275377875095861710925207028551771520610387238734819759256223080175603032167658086669886661302962985046348865181740591251321966682848536331583243529
求明文m?

解题:

#!/usr/bin/python 
#coding:utf-8 
#@Author:Mr.Aur0ra
 
import gmpy2  
import libnum  
c = 9217979941366220275377875095861710925207028551771520610387238734819759256223080175603032167658086669886661302962985046348865181740591251321966682848536331583243529  
m = gmpy2.isqrt(c)  
m = int(m)  
m_text = libnum.n2s(m)  
print(m_text)

3. e=2 Rabin加密中的N可被分解

Rabin解密的Python实现:

def rabin_decrypt(c, p, q, e=2):  
    n = p * q  
    mp = pow(c, (p + 1) / 4, p)  
    mq = pow(c, (q + 1) / 4, q)  
    yp = gmpy2.invert(p, q)  
    yq = gmpy2.invert(q, p)  
    r = (yp * p * mq + yq * q * mp) % n  
    rr = n - r  
    s = (yp * p * mq - yq * q * mp) % n  
    ss = n - s  
    return (r, rr, s, ss)  

题目: 02-Jarvis OJ -Crypto-Hard RSA

 

ValueError: no invmod for given @a and @n 

所以要多积累一些题型，这里就是考察的e=2时，Rabin加密中的N可被分解。

首先通过openssl提取公钥的信息：

我们得到e=2，n=0xC2636....

然后分解n得到p和q：

然后就可以写Python脚本了:

#!/usr/bin/python 
#coding:utf-8 
 
import gmpy2  
import libnum  
 
e = 2  
n = 87924348264132406875276140514499937145050893665602592992418171647042491658461  
p = 275127860351348928173285174381581152299  
q = 319576316814478949870590164193048041239  
c=int(open('./flag.enc','rb').read().encode('hex'),16)  
 
mp=pow(c,(p+1)/4,p)  
mq=pow(c,(q+1)/4,q)  
yp=gmpy2.invert(p,q)  
yq=gmpy2.invert(q,p)  
r=(yp*p*mq+yq*q*mp)%n  
rr=n-r  
s=(yp*p*mq-yq*q*mp)%n  
ss=n-s  
print libnum.n2s(r)  
print libnum.n2s(rr)  
print libnum.n2s(s)  
print libnum.n2s(ss) 

4， e=3 小明文攻击

适用情况：e较小，一般为3。

5，Roll按行加密

顾名思义，这里的的加密是按行进行的。

题目: 04-实验吧---RSAROLL

不要总是觉得 密文C 就是一连串的字符串，密文C 也可以是分行的，记住不要把分行符删除让 密文C 变为一个字符串。应该按行进行解密。

ｎ为920139713，ｅ为19，手动把加密的部分另存为一份文件roll.txt。

解题脚本：

#!/usr/bin/python 
#coding:utf-8 
#@Author:Mr.Aur0ra
 
import gmpy2  
from Crypto.Util.number import long_to_bytes  
 
n = 920139713  
p = 49891  
q = 18443  
e = 19  
phi = (p-1)*(q-1)  
d = gmpy2.invert(e,phi)  
m = ""  
with open('roll.txt','r') as f:  
    for c in f.readlines():  
    m += long_to_bytes(pow(int(c), d, n))  
print m  

6，模不互素

适用情况：存在两个或更多模数 ，且gcd(N1,N2)!=1 也就是N1和N2不互质。

多个模数n共用质数，则可以很容易利用欧几里得算法求得他们的质因数之一gcd(N1,N2) ，然后这个最大公约数可用于分解模数分别得到对应的p和q，即可进行解密。实现参照本文欧几里得算法 部分和RSA解密部分。

题目: 05-存货1

N is 18674375108313094928585156581138941368570022222190945461284402673204018075354069827186085851309806592398721628845336840532779579197302984987661547245423180760958022898546496524249201679543421158842103496452861932183144343315925106154322066796612415616342291023962127055311307613898583850177922930685155351380500587263611591893137588708003711296496548004793832636078992866149115453883484010146248683416979269684197112659302912316105354447631916609587360103908746719586185593386794532066034112164661723748874045470225129298518385683561122623859924435600673501186244422907402943929464694448652074412105888867178867357727
e is 65537
message is 0x8BD7BF995BF9E16A0D04ADB49A2411C74FFDB0DB4F35DB3A79A1B44691947C9824085BC4CA5F7F4EFA3C8FD0BC3E870AA6D5E15307A63A2172C44C5903D35785B8D06B51651EE7106B070D5A6AABA089AB67609661265B74914C865F863DC1D2DC08CE0B026107A74EC3FDC62666B50110B9D15A243EAAD6F53646929A3369285404868E42DD0BBE92D956018E3C0B36EF5E9516E433228CFDD06D6E662EC0A9A31061EA11F61CA17EABF43D2D4977FC9D6FC53AB6DC01509401B8D9A46B59A9ADAA97D54CC50C27445E4C21B893510620EC3566AD6E8727FA147437B207505217E6F2DF009E2286C8354D281374D7802D08A2062FE48DBF135BBCAB120EBF84

N is 20071978783607427283823783012022286910630968751671103864055982304683197064862908267206049336732205051588820325894943126769930029619538705149178241710069113634567118672515743206769333625177879492557703359178528342489585156713623530654319500738508146831223487732824835005697932704427046675392714922683584376449203594641540794557871881581407228096642417744611261557101573050163285919971711214856243031354845945564837109657494523902296444463748723639109612438012590084771865377795409000586992732971594598355272609789079147061852664472115395344504822644651957496307894998467309347038349470471900776050769578152203349128951
e is 65537
message is 0x8C3CF3161AA3E37831030985C60566A7604688B73E5B1D3B36E72EF06ED4F71289EFE80E0D94BD755034E6C210F17DA85B9D0388F3AD104C68BC514A8EB1569A109EB5F266F7C5FA4DDFA638258949B43D4CF1406720CCD4CA11E74FDF8AEB35C56A79781C87157FC4213573329C5B0FF411F8A4F34580AA103DB9FD403C0D409FA11860A7C4595FDC49DC2CF94E5112B772E5DEC8F17E24B10A7FD7A95DCB87BE5E27C32FC931574A7847BC506A61EFE9DB3D3F612143845FE80D7B3EA548B886A67A29CBDB2775B1F91178B6DA763F1A6ECFF46592E4C7FFAAB6C9FEF29D9CB9E035A3D98ECFFB26BA2EEAA56D1CD096E6A2CF9A58086CAD7718DDA5CB0C1B

求明文m？

这里把明文字符串一分为二做了分别做了RSA加密，上面的message其实就是密文c。关键是加密时它们多个模数使用了相同的质数e，而且模数N1和N2不互素，所以可以进行模不互素攻击。

判断两个数是否互素的脚本:

#!/usr/bin/python 
#coding:utf-8 
#@Author:Mr.Aur0ra
 
def gcd(a,b):    #判断来两个数是否互素,辗转相除法 
    if(b==0):  
        return a  
    else:  
        return gcd(b,a%b)  

def main():  
    x = 17              #x,y的值根据需要修改即可 
    y = 65537  
    if gcd(x,y)==1:    #如果两个数的最大公约数是1，那么两数互素。 
        print str(x)+" "+str(y) + "两个数互素" 
    else:  
        print str(x)+" "+str(y) + "两个数不互素" 
if __name__=="__main__":  
    main()

题目是给出的文件rsa2.txt，为了方便Python直接读取文件为变量赋值，这里把无关的解释性东西删除掉，生成新的tmp.txt文件。

内容如下:

解题脚本:

#!/usr/bin/python  
#coding:utf-8  
#@Author:Mr.Aur0ra
  
import gmpy2  
from Crypto.Util.number import long_to_bytes  
  
lines = open('tmp.txt','r').readlines()  
  
c1 = int(lines[2],16)  
c2 = int(lines[6],16)  
n1 = int(lines[0])  
n2 = int(lines[4])  
  
p12 = gmpy2.gcd(n1, n2)  
assert (p12 != 1)  
q1 = n1 / p12  
q2 = n2 / p12  
e = 0x10001  
d1 = gmpy2.invert(e, (p12 - 1) * (q1 - 1))  
d2 = gmpy2.invert(e, (p12 - 1) * (q2 - 1))  
m1 = pow(c1, d1, n1)  
m2 = pow(c2, d2, n2)  
print long_to_bytes(m1)+long_to_bytes(m2)

7，共模攻击

适用情况：明文m、模数n相同，公钥指数e、密文c不同，gcd(e1,e2)==1也就是e1和e2互质。

对同一明文的多次加密使用相同的模数和不同的公钥指数可能导致共模攻击。

题目: 06-Jarvis OJ -Crypto-very hard RSA

这个题目就比较有意思了，4096位的RSA加密，要不是这里存在共模攻击说不定你死活都解不开。哈哈哈，要是有量子计算机的话说不定能解开。

题目给出了两个flag.enc文件以及一个easyRSA.py的加密脚本。

通过分析加密脚本可知，该加密脚本首先会从flag.txt中读取字符串flag，然后对flag根据不同的e的值进行2次RSA加密，并分别将密文保存到了flag.enc1和flag.enc2中。

我们发现明文m、模数n相同，但是公钥指数e1和e2不同，而且e1与e2互素（上面给过判断2数是否互素的脚本），所以这就是典型的共模攻击。

解密脚本

8,低解密指数攻击

在RSA中d也称为解密指数，当d比较小的时候，e也就显得特别大了。

适用情况：e过大或过小（一般e过大时使用）

在e过大或过小的情况下，可使用算法从e中快速推断出d的值，进而求出m

题目: 07-存货2

n = 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597L
e = 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619L
c = 38230991316229399651823567590692301060044620412191737764632384680546256228451518238842965221394711848337832459443844446889468362154188214840736744657885858943810177675871991111466653158257191139605699916347308294995664530280816850482740530602254559123759121106338359220242637775919026933563326069449424391192
求明文m?

首先需要需要下载工具rsa-wiener-attack ：

git clone https://github.com/pablocelayes/rsa-wiener-attack

然后把exp.py放入这个目录中运行即可：

低解密指数攻击

9,根据公钥计算得到私钥

这种题型需要使用RsaCtfTools根据公钥生成私钥

题目: 08-存货3

题目只给出了两个文件（一个私钥文件和一个密文文件）

按照常规查看提取一下公钥文件，发现n特别大，无法直接分解为p和q，而且e也不存在是特殊值的可能，也不存在其他的攻击方法。

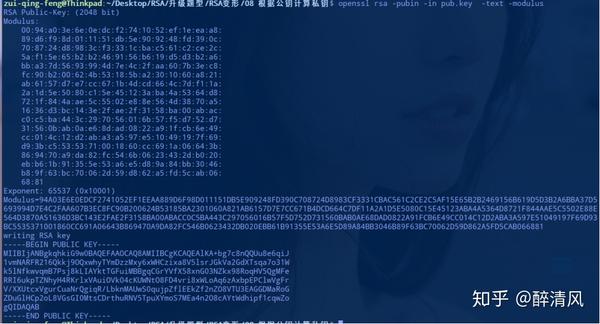
首先进入RsaCtfTools，接着执行下面的命令生成私钥。

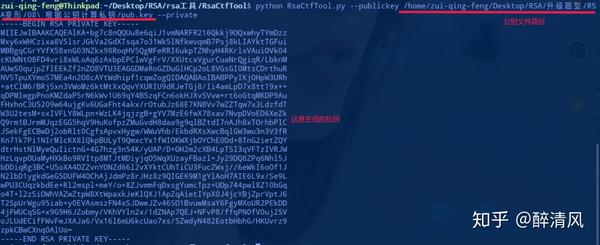
接着把这些内容复制到新创建的文件pri.key中。

使用openssl通过私钥文件进行解密：

打开生成的文件txt即可得到flag

作者：曙光
链接：https://zhuanlan.zhihu.com/p/76228394
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

10,分解n得到相同的几个p

这个题目牵扯到欧拉函数的一些知识，一会你就知道该补一补了，哈哈哈。

题目: 09-存货4

题目给出两个文件，一个文件是加密脚本encrypt.py，另一个是加密脚本输出的文件2.txt。

下面是我注释了的加密脚本:

import gmpy2
import random
from Crypto.Util.number import *
from flag import flag

def generate_key(1024):
    p = getPrime(1024)
    r = random.randint(2, 10)
    s = random.randint(r, 1024)
    while True:
        e = random.randint(3, p**r*(p-1))
        if gmpy2.gcd(e, p**s*(p-1)) == 1:
        	break
    pubkey = (long(e), long(p**r))   #返回e和p^r
    return pubkey

def crypt(msg, pubkey):
    e, n = pubkey             #e,n=p^r
    m = bytes_to_long(msg)    
    assert m < n - 1
    enc = pow(m, e, n)       
    return long_to_bytes(enc)

nbit = 1024
pubkey = generate_key(1024)
print 'pubkey =', pubkey  #输出e和p^r
msg = flag值   
enc = crypt(msg, pubkey)  

print 'enc =\n', enc.encode('base64')

11,已知n,e,d求p,q

一看这个标题你就应该有个觉悟，n一定无法直接分解得到p和q。

题目: 10-存货5

题目给出了两个文件，一个是加密脚本chall.py，一个是加密后输出的内容output.txt。

分析一下加密脚本：

加密脚本真的是很简单啊，flag就是str(p+q)进行md5运算之后的得到的字符串，从output.txt中可以得到n,e,d。

作者：曙光
链接：https://zhuanlan.zhihu.com/p/76228394
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

低加密指数广播攻击

如果选取的加密指数较低，并且使用了相同的加密指数给一个接受者的群发送相同的信息，那么可以进行广播攻击得到明文。

适用范围：模数n、密文c不同，明文m、加密指数e相同。一般情况下，e=k (k是题目给出的n和c的组数)。

题目: 12-Jarvis OJ -2018强网杯nextrsa-Level9

题目给出n1，n2，n3，c1，c2，c3，e。求明文m的值。

 

 

标签：gmpy2,17,题目,RSA,2023.2,flag,import,print,加密
From： https://www.cnblogs.com/wlwl1234/p/17131490.html