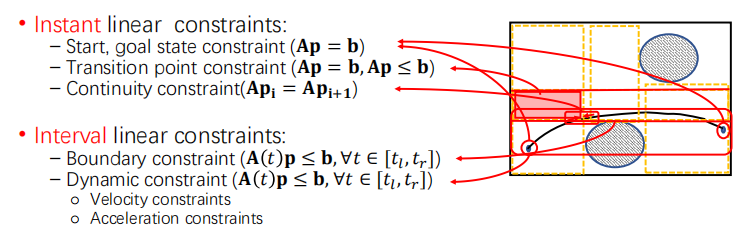基于Minimum Snap/Jerk的轨迹生成/优化
轨迹生成/优化
寻找一条路径,可以不考虑动力学约束,也可以考虑动力学约束,然后将路径所在的低维空间转到机器人运动的状态空间,称为轨迹生成
生成一条【安全】、【动力学可行】、【光滑】的轨迹是motion planning的终极目标
为什么要求轨迹平滑?
- 便于机器人移动
- 速度/更高阶的动力学参数(加速度,jerk……)不能突变
- 机器人不能再拐角处停下来(如果用直线来连接,轨迹在拐角处发生突变,机器人就需要停下来,转到下一段直线)
- 更节约能量(不用频繁加减速)
path finding + trajectory generation
经典的planning包括【前端路径搜索】+【后端轨迹生成】
我们已经有了kinodynamic planning,搜索出来的路径满足动力学约束,为什么还要进行轨迹生成?
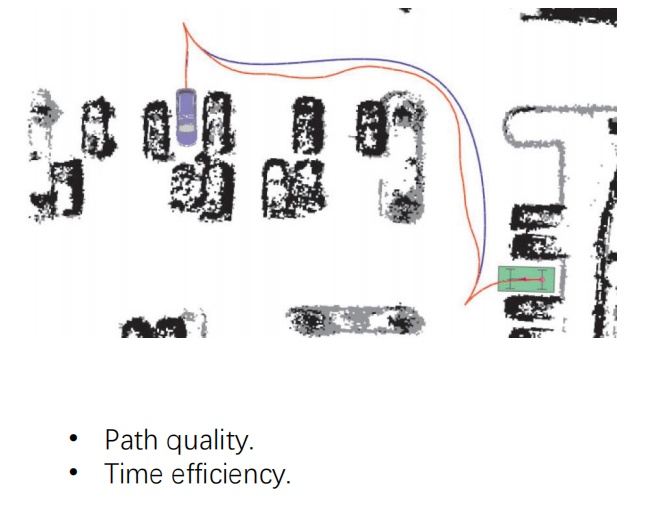
如图:橙色的是Hybrid A*生成的轨迹,蓝色是优化后的,二者都可以直接执行,但是明显蓝色更优一些,如果算例有限,那么kinodynamic path也可以不做轨迹优化,但是如果算例足够,可以通过比较小的代价进行轨迹优化,那么做轨迹优化显然是更好的选择
框架
- 边界条件:起始的状态,目标的状态
- 中间条件:中间路点(waypoins)的状态
- waypoints可以人为给出
- 也可以是前端path finding出来的(A*,RRT,etc)
- 光滑条件:每个point的左右状态极限是连续的,也就是minimize变化率
Minimum Snap Optimization
Differentia Flatness 微分平坦
一个全维度的状态空间可以被一组低维的精心挑选的输出平坦空间的变量及其导数的代数组合的方式所表示。由此,路径规划就可以在这组精心挑选的变量的空间所进行。
例如:对于四旋翼飞机来说,状态空间是12维度,包括3个位置,3个角度,3个线速度,3个角速度。可以用3个位置和偏航角(x,y,z,yaw)这4个量(对于无人车需要x,y,yaw)及其导数表示。所以,路径规划可以在4维空间中进行,无人车可以在【(x,y,yaw)】的三维空间进行规划。
多项式轨迹
轨迹选择多项式来表示,用多项式来表示轨迹的好处:
1)多项式的光滑准则很好,例如某阶导数的平方的积分
2)求导好求,能快速求出v,a,jerk……
3)3维度方向上都是多项式,可以方便的解耦地规划
平滑一段1-D轨迹
其实就是之前的BVP问题
- 多项式函数具有天然的光滑性
- 没有waypoints
因此就是这样一个问题,以五次多项式轨迹为例:
\[x = p_5x^5+p_4x^4+p_3x^3+p_2x^2+p_1x+p_0 \]- 边界条件
| Position | Velocity | Acceleration | |
|---|---|---|---|
| t = 0 | a | 0 | 0 |
| t = T | b | 0 | 0 |
- 求解
平滑多段1-D轨迹
- 对直线段的拐角处进行平滑
- 给定waypoints的速度v
- waypoints的加速度为0
- 需要特殊处理短段(short segments)
问题则变成
\[\begin{align}x &= p_5x^5+p_4x^4+p_3x^3+p_2x^2+p_1x+p_0 \\v &= 5p_5x^4+4p_4x^3+3p_3x^2+2p_2x+p_1\end{align} \]- 边界条件
| Position | Velocity | Acceleration | |
|---|---|---|---|
| t = 0 | a | v0 | 0 |
| t = T | b | vr | 0 |
- Solve
waypoints的【v,a】是人为指定的,但是实际上我们并不知道waypoints的v,a应该是多少,那么就需要用【优化的方式】找出每个waypoint最优的【v和a】
Optimization-based Trajectory Generation
Minimize Snap Optimization
- 对于四旋翼无人机,Minimize Jerk 就是Minimize 角速度,有利于视觉跟踪
- 对于四旋翼无人机,Minimize Snap就是Minimize 推力差,有利于节省能量
- 对于无人车,一般是Minimize Jerk ,有利于乘坐舒适性
问题定义:
\[f(t)=\left\{\begin{array}{cc}f_{1}(t) \doteq \sum_{i=0}^{N} p_{1, i} t^{i} & T_{0} \leq t \leq T_{1} \\f_{2}(t) \doteq \sum_{i=0}^{N} p_{2, i} t^{i} & T_{1} \leq t \leq T_{2} \\\vdots & \vdots \\f_{M}(t) \doteq \sum_{i=0}^{N} p_{M, i} t^{i} & T_{M-1} \leq t \leq T_{M}\end{array}\right. \]- 每段都是一个多项式
- 并不要求每一段的阶数都是一样的,但是如果令每一段多项式的阶数保持一致,就会使问题简单化
- 每一段的时间都是要已知的,不是像OBVP问题时间是优化出来的
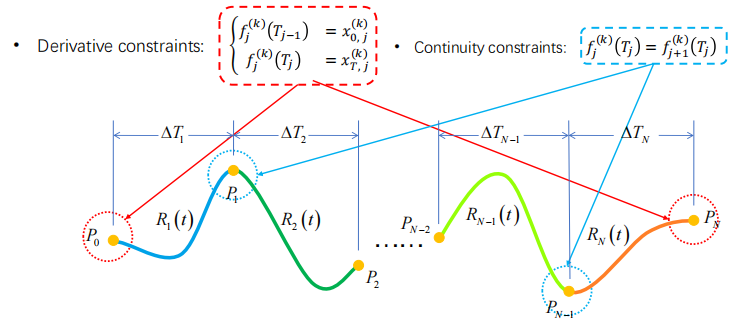
约束条件
- 微分约束
- 连续性约束
确定轨迹多项式的阶次
【光滑性:k阶光滑意味着k-1阶连续】
标准:
-
在某一阶次上光滑
-
在某一阶次上连续
-
在某一阶次上,优化控制输入
以上三个条件是相互独立的
对于一段轨迹:
- Minimize Jerk: N = 2 * 3(jerk) - 1 = 5, control input p, v, a
- Minimize Snap: N = 2 * 4(Snap) - 1 = 7, control input p, v, a, j
对于k段轨迹:
以Minimize Jerk为例:
- 约束:起点和终点各有3个约束(\(p_0,v_0,a_0,p_f,v_f,a_f,f \ for final\)),中间k-1个waypoint提供了位置约束,因此约束的个数为:\(3+3+k-1=k+5\)
- 未知量个数:一共有k段轨迹,每段轨迹有N+1个未知量,因此未知量的个数为\((N+1)*k\)
- \((N+1)*k=k+5\),得到\(N=5/k\)
m可以看出,随着轨迹段数的增加,平均的阶次是降低的,但是实际上在工程中,我们不知道前端路径搜索会返回几个waypoint,可能直接返回了终点,因此需要做最坏的准备,因此通常每段都取成5阶
时间轴
时间的定义决定了轨迹多项式函数的形式,有两种方式:
-
相对时间,数值是稳定的,但是多项式复杂

-
绝对时间,多项式简洁,但是数值不稳定

Minimize Snap
定义cost function:
\[\begin{aligned}& f(t)=\sum_i p_i t^i \\& \Rightarrow f^{(4)}(t)=\sum_{i \geq 4} i(i-1)(i-2)(i-3) t^{i-4} p_i \\& \Rightarrow\left(f^{(4)}(t)\right)^2=\sum_{i \geq 4, l \geq 4} i(i-1)(i-2)(i-3) l(l-1)(l-2)(l-3) t^{i+l-8} p_i p_l \\& \Rightarrow J(T)=\int_{T_{j-1}}^{T_j}\left(f^4(t)\right)^2 d t=\sum_{i \geq 4, l \geq 4} \frac{i(i-1)(i-2)(i-3) j(l-1)(l-2)(l-3)}{i+l-7}\left(T_j^{i+l-7}-T_{j-1}^{i+l-7}\right) p_i p_l \\& \Rightarrow J(T)=\int_{T_{j-1}}^{T_j}\left(f^4(t)\right)^2 d t \\& \Rightarrow J_j(T)=\mathbf{p}_j^T \mathbf{Q}_j \mathbf{p}_j \text { Minimize this! } &\end{aligned} \]约束
- 微分约束,对于起点和终点是k = 0, 1, 2, 3,即要求p,v,a,j;对于waypoint则通常要求k = 0,即只要求p,这两种情况都可以写成矩阵形式的等式约束
- 连续性约束,对于waypoint虽然不要求v,a,j,但是要求左右两段的轨迹在waypoint处的各阶导数是相等的
整合成QP问题
\[\begin{aligned}& \min \left[\begin{array}{c}\mathbf{p}_1 \\\vdots \\\mathbf{p}_M\end{array}\right]^T \quad\left[\begin{array}{ccc}\mathbf{Q}_1 & \mathbf{0} & \mathbf{0} \\\mathbf{0} & \ddots & \mathbf{0} \\\mathbf{0} & \mathbf{0} & \mathbf{Q}_M\end{array}\right]\left[\begin{array}{c}\mathbf{p}_1 \\\vdots \\\mathbf{p}_M\end{array}\right] \\& \text { s.t. } \mathbf{A}_{\mathrm{eq}}\left[\begin{array}{c}\mathbf{p}_1 \\\vdots \\\mathbf{p}_M\end{array}\right]=\mathbf{d}_{e q}&\end{aligned} \]QP问题(二次优化问题)是一种典型的凸优化问题,在无人驾驶中非常常见。
简单凸优化问题
具体凸优化的课程可以看中科大凌青老师课程和Boyd斯坦福公开课程
- 凸优化问题的标准形式
其中目标函数\(f_0\)和不等式约束函数\(f_i\ (i = 1,\dots,m)\)都是凸函数,\(Ax = b\)要求是仿射的,x的定义域要是一个凸集
- 几种标准的凸优化问题
- Linear Programming (LP):线性规划问题
- Quadratic Programming (QP):二次规划问题
- Quadratically Constrained QP (QCQP):具有二次约束的二次规划问题
- Second-Order Cone Programming (SOCP):二阶最优化问题
Closed-form Solution to Minimum Snap
利用QP求解器求解的是Minimum Snap问题的数值解,另一种解法,从代数上直接求出Minimum Snap问题的解析解,即Minimum Snap问题的闭式解法。
变量映射
之前优化的变量是每一段轨迹多项式的系数\(p_{j,0},p_{j,1},\dots,p_{j,7}\),这样做的问题是,优化的参数不具有具体的物理意义,会带来轨迹优化上的数值不稳定,例如\(p_{7}t^7\),由于\(t^7\)很大有可能优化出来的\(p_7\)非常非常小。因此可以将原问题从优化【轨迹参数】问题转变成优化各个【路点的导数约束】的问题。通过映射矩阵\(M\)将轨迹参数\(p_j\)映射到路点的导数约束\(d_j\),即\(p_jM=d_j\)。
- 原问题的目标函数:
- 映射关系:
- 新的目标函数:
- 轨迹方程:
- 得到映射矩阵M
【这里的时间用的是相对时间】
固定变量和自由变量分解
起点和终点的【p,v,a,j】,以及waypoint的【p】都是已知的固定的,因此可以通过非奇异选择矩阵\(C\)将优化变量d进行分解。
\[\mathbf{C}^T\begin{bmatrix}\mathbf{d}_F\\ \mathbf{d}_P\end{bmatrix}=\begin{bmatrix}\mathbf{d}_1\\ \vdots\\ \mathbf{d}_M\end{bmatrix}\ d_P\ for free\ and\ d_F\ for\ fixed \]因此目标函数变成一个无约束的二次规划问题,可以闭式求解:
\[J=\begin{bmatrix}\mathbf{d}_F\\ \mathbf{d}_P\end{bmatrix}^T\mathbf{C}M^{-T}\mathbf{Q}M^{-1}\mathbf{C}^T\begin{bmatrix}\mathbf{d}_F\\ \mathbf{d}_P\end{bmatrix}=\begin{bmatrix}\mathbf{d}_F\\ \mathbf{d}_P\end{bmatrix}^T\begin{bmatrix}\mathbf{R}_{pF}&\mathbf{R}_{pp}\\ \mathbf{R}_{pF}&\mathbf{R}_{pp}\end{bmatrix}\begin{bmatrix}\mathbf{d}_F\\ \mathbf{d}_p\end{bmatrix} \]\[\begin{array}{c}J=\mathbf{d}_F^T\mathbf{R}_{F F}\mathbf{d}_F+\mathbf{d}_F^T\mathbf{R}_{F P}\mathbf{d}_P+\mathbf{d}_P^T\mathbf{R}_{P F}\mathbf{d}_F+\mathbf{d}_P^T\mathbf{R}_{P P}\mathbf{d}_P\\ \\ \mathbf{d}_P^*=-\mathbf{R}_{P P}^{-1}\mathbf{R}_{F P}^T\mathbf{d}_F\end{array} \]【为什么连续性约束也消失了?因为通过设计选则矩阵C将\(d_F\)中的一个变量映射到d的两个变量中去,这样就满足了连续性约束】
【设计选择矩阵C】

分级方法
path planning + trajectory generation
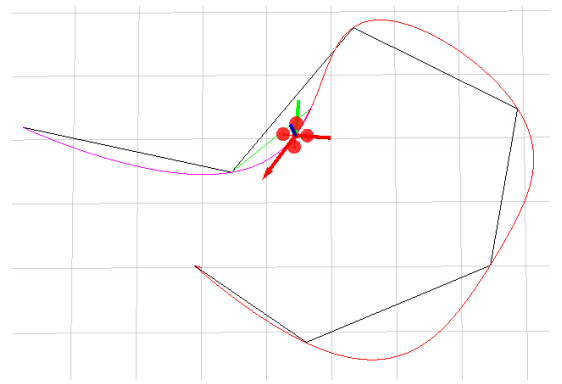
- 如何获得无碰撞的waypoint:path planning
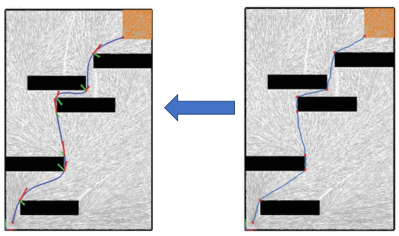
图中展示的是RRT进行路径规划得到waypoints,接着利用minimum snap进行轨迹生成
- 利用RRT寻找的路径是无碰撞的,但是经过轨迹优化后会产生超调(如图),如何确保优化后的轨迹是无碰撞的?
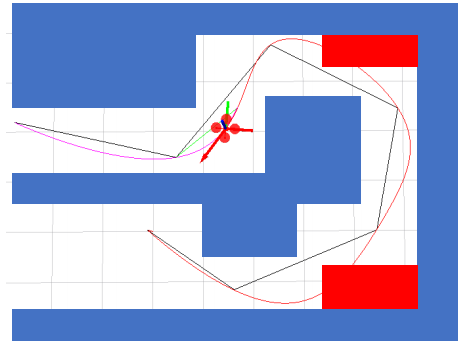
解决方案:在碰撞的部分新增一个路点,重新生成轨迹,如果还是碰撞,就继续从插入路点,极端情况生成的轨迹会无限接近于path planning出的绝对安全的路径
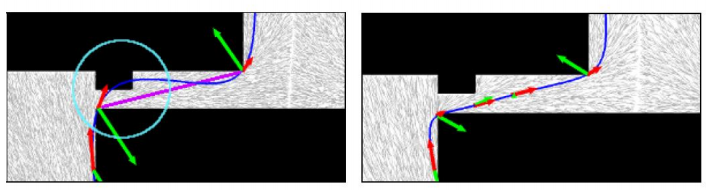
更好的解决方案:增加路点的方案,会造成局部轨迹的质量快速下降,且无法保证,通过加点一定可以将轨迹控制在绝对安全的范围内。更好的做法是添加bounding box约束,在下节课详细讨论。