Author: Wublabdubdub
随机化
解决关于随机化的是什么,为什么,怎么做的问题
什么是随机化
随机化算法(\(\mathcal{randomized\ algorithm}\)),是这样一种算法,在算法中使用了随机函数,且随机函数的返回值直接或者间接的影响了算法的执行流程或执行结果。就是将算法的某一步或某几步置于运气的控制之下,即该算法在运行的过程中的某一步或某几步涉及一个随机决策,或者说其中的一个决策依赖于某种随机事件。
————《百度百科》(不是给人看的)
啥意思?
就如它的名字一样,就是使用了随机函数的算法。 可以笼统的认为就是算法中用到了随机数并影响了结果(包括结果和资源消耗)就是随机化
随机化算法大体可以分为蒙特卡罗算法,拉斯维加斯算法、和舍伍德算法。(这里的的分类都并非指具体代码实现,而是思想)
特点:一般来讲同一段随机化算法即使在同一运行环境下多次进行,也有可能产生不同的结果,结果精度或正确性会随运行次数增加而增加,相应地时间也会更长
蒙特卡罗算法
蒙特卡罗算法用于求问题的准确解。对许多问题,近似解是毫无意义的。用蒙特卡罗算法能求得问题的一个解,但这个解未必是正确的。其求得正确解的概率依赖算法所用的时间。算法所用时间越多,得到正确解的概率就越高。蒙特卡罗算法的主要缺点也在于此。一般情况下,无法有效的判断所得到的解是否可定正确。大多数蒙特卡罗算法经重复调用之后正确率快速上升。
例如:随机抛点求圆周率
原理:
现在我们有一个半径为 \(r\) 圆和他的外接正方形,设圆的面积为 \(S_1\) 正方形面积为 $ S_2 $
我们随机向平面内扔sum个点,每个点落在圆内的概率为\(\frac{S_1}{S_2}\)
则
\[S_1=\pi r^2,S_2=4 r^2 \]\[\frac{cnt}{sum}= \frac{S_1}{S_2}=\frac{\pi}{4} \]当sum足够大时cnt/sum*4就是pi的值
Code:
#include<iostream>
#include<cstdio>
#include<random>
#include<time.h>
#include<cmath>
using namespace std;
//求解圆周率的值
double sum=0;//一共sum个点
double cnt=0;//cnt个在圆内
int times;//扔times次
int main()
{
mt19937 rd(time(0));//生成随机数
cin>>times;
sum=times;//记录次数
while(times--)
{
double x=((long long)rd())%10000000;
double y=((long long)rd())%10000000;
//生成一个点
cnt+=(sqrt((x-5000000.00)*(x-5000000.00)+(y-5000000.00)*(y-5000000.00))<=5000000.00);
//看是否在圆内
}
cout<<cnt/sum*4.00;//输出
return 0;
}
//这样做精度极低,实际生产应用时我们自然不会这样做
//仅需理解它作为蒙特卡罗算法的特征以及作为随机化算法的可行性即可
拉斯维加斯算法
拉斯维加斯算法不会得到不正确的解。一旦用拉斯维加斯算法找到一个解,这个解就一定是正确解。但有时用拉斯维加斯算法会找不到解。拉斯维加斯算法找到正确解的概率会随着它所用的计算时间的增加而提高。
例如:猴子排序
依据:无限猴子定律(一只猴子随机敲打打字机键盘,如果时间足够长,总是能打出特定的文本,比如莎士比亚全集。)
因此我们让一个序列反复打乱,总会有一次有序
Code:
#include<algorithm>
#include<iostream>
#include<random>
#include<cstdio>
using namespace std;
int a[100002];
int main()
{
mt19937 r(time(0));
int n;scanf("%d",&n);
bool b=1;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
while(b)
{
shuffle(a+1,a+1+n,r);//随机打乱
b=0;
for(int i=2;i<=n;i++)//是否有序
if(a[i]<a[i-1])
{
b=1;break;//有序则跳出
}
}
for(int i=1;i<=n;i++) printf("%d ",a[i]);
return 0;
}
//这样做速度极慢,实际生产应用时我们自然不会这样做
//仅需理解它作为拉斯维加斯算法的特征以及作为随机化算法的可行性即可
舍伍德算法
舍伍德算法总能求得问题的一个解,而且所得的解总是正确的。当一个确定性算法在最坏情况下的计算复杂性与其平均情况下的计算复杂性有较大差别时,可在这个确定性算法中引入随机性将它改造成一个舍伍德算法,消除或减少问题的好坏实例间的这种差别。舍伍德算法的精髓不是避免算法的最坏情形,而是设法消除这种最坏情形行为与特定实例之间的关联性。
快速排序就是一个例子,在快速排序中我们选取的标准数在答案序列中的大小是随机的,因此即使答案不变(总会是一个有序序列),所消耗的时间是不一定的(如果恰好每次选取的基准数都恰好为最大的数或最小的数,快排会退化为 \(\mathcal{n^2}\))
为了避免出题人刻意制造这种情况(事实上,这么优(que)秀(de)的出题人可以扔海里喂鲨鱼了),可以先用shuffle打乱顺序
另外,treap也可以被视作一个舍伍德算法
代码就不放了。
//这样做速度没啥影响,实际生产应用时我们自然可以这样做
//仅需理解它作为舍伍德算法的特征以及作为随机化算法的可行性即可
为什么使用随机化算法
- 有些问题难以在一个确定的时间内给出正确解,但使用随机化可以在较短时间内给出一个近似解,并且在误差在接受范围内(最速曲线的计算,PI的计算)。
- 考试时乱搞(为了得分嘛,不寒掺)
- 对由于一些原因被证伪的贪心,进行改造,使它合理起来,即随机化贪心。(P7883 ,P2503)
如何写随机化算法
随机函数
既然要用随机化,自然要有一个产生随机数或随机序列的方式
rand( )
包含于头文件
mt19937
温馨提示:使用mt19937需要c++14及以上的版本
一种更快更好的随机数产生方式在头文件mt19937 myrand(time(0)) (其中"myrand"可以换为任意您喜欢的名字)每次使用时打出myrand()即可,范围为unsigned int内的整数,如果想让随机化范围达到unsigned long long,可使用mt19937_64
shuffle
用于打乱一个数组,使用方法为shuffle(a+1,a+1+n,myrand())打乱a数组中1~n位置的元素,myrand()为mt19937生成的随机数函数
模拟退火
模拟退火算法来源于固体退火原理,是一种基于概率的算法,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
————《百度百科》(依然看不懂)
人话:模拟退火又叫模拟退役(bushi)
伪代码如下
得到一个初始解ans
设定一个合适的温度
while(温度还不够低)
{
产生新解
if(新解更优) 采纳新解,更新状态
else if(新解与旧解的差符合一定条件(Metropolis准则)) 更新状态
降温
}
其中Metropolis准则为:
计算概率$$ P = exp(-\frac{f(x + 1)-f(x)}{T_0}) $$。取一个随机数\(0<r<1\),当$ r < P$ 时把当前值更新为新值,否则不更新。可以发现,当前温度 \(T_0\)越大,指数函数括号里的值越大,接受这个新值的概率P越大。随着迭代次数的增加,\(T_0\)会越来越小,接受新值的概率P也会越来越小,相当于渐渐冷却了下来,趋于稳定的状态。
这么来看仍然有些太抽象了,我们来看一道例题:
洛谷P1337 吊打dpc
[JSOI2004] 平衡点 / 吊打dpc
题目描述
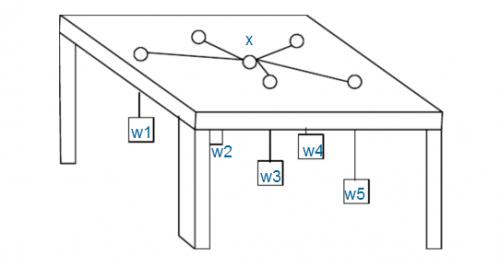
如图,有 \(n\) 个重物,每个重物系在一条足够长的绳子上。
每条绳子自上而下穿过桌面上的洞,然后系在一起。图中 \(x\) 处就是公共的绳结。假设绳子是完全弹性的(即不会造成能量损失),桌子足够高(重物不会垂到地上),且忽略所有的摩擦,求绳结 \(x\) 最终平衡于何处。
注意:桌面上的洞都比绳结 \(x\) 小得多,所以即使某个重物特别重,绳结 \(x\) 也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
明确一点:能量越小的系统越稳定,最终状态指的就是使得系统动能最小的点
就是让你找一个点\((x_0,y_0)\)使$$\sum_{i=1}{n}{\sqrt{(x_i-x_0)2+(y_i-y_0)^2}*w_i}$$最小
Solution 1
最暴力的做法
以0.001为增量,枚举横纵坐标,记录答案
预计\(0pts\)
Solution 2
正解
利用计算几何知识二分,参考题解区
我相信讲计算几何或者二分的大佬会给出正解的
Solution 3
模拟退火
选择坐标平均值位置作为初始解,每次降温更改坐标并重新计算
#include<iostream>
#include<random>
#include<cstdio>
#include<cmath>
#include<time.h>
using namespace std;
const long long R_M=20221027;//草神的祝福
int n;
mt19937 mrd(time(0));//随机数函数
struct node
{
int x,y,w;
}a[2002];
double ansx,ansy,answ;
double eee(double x,double y)//计算系统能量
{
double res=0,dx,dy;
for(int i=1;i<=n;i++)
{
dx=x-a[i].x;
dy=y-a[i].y;
res+=sqrt(dx*dx+dy*dy)*a[i].w;
}
return res;
}
long long rd()//手动限制mt19937范围
{
return (long long)mrd()%R_M;
}
void solve()//退火主体
{
double t=4500;//初温,参数1
while(t>1e-15)//末温,参数2
{
//产生一个新解
double ex=ansx+(rd()*2-R_M)*t;
double ey=ansy+(rd()*2-R_M)*t;
double nans=eee(ex,ey);
//计算差值
double de=nans-answ;
if(de<0)//更优
{
//采纳
ansx=ex;
ansy=ey;
answ=nans;
}
else if(exp(-de/t)*R_M>rd())//概率接受
{
//只更新状态,不改变答案
ansx=ex;
ansy=ey;
}
t*=0.997;//降温,参数3
}
return ;
}
void work()
{
//矩阵提精(bushi)
solve();solve();solve();solve();
solve();solve();solve();solve();
solve();solve();solve();solve();
solve();solve();solve();solve();
}
int main()
{
cin>>n;//读入
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].w);
ansx+=a[i].x;
ansy+=a[i].y;
}
//产生初始解
ansx/=n;
ansy/=n;
answ=eee(ansx,ansy);
//模拟退火
work();
//输出
printf("%.3lf %.3lf",ansx,ansy);
return 0;
}
代码中标出了三个参数,其中初始温度足够高就行,末温一般在\(10^{-10}\)以下,降温速度最直接地影响代码运行时间,降温速度越快,程序越快,精度越低,降温速度越慢(越接近1),程序越慢,精度越高,模拟退火的参数会极大地影响正确率,调得一个好参会花费大量时间,\(IOI\)赛制中可以通过不断尝试来取得AC,但在\(OI\)赛制中,模拟退火想获得AC极不容易,但是作为一个骗分手段,往往可以获得\(60-80pts\)的好分数。
题外话:有人说随机化是对一道好题的不敬,我说要是会写正解我自然会表示出对该题的敬意(摘自luogu题解区)
随机化贪心
通过随机,使得一些可以被轻易hack掉的贪心可行
话不多说,上例题:
题目描述
已知 \(n\) 个正整数 \(a_1,a_2 ... a_n\) 。今要将它们分成 \(m\) 组,使得各组数据的数值和最平均,即各组数字之和的均方差最小。均方差公式如下:
\[\sigma = \sqrt{\frac 1m \sum\limits_{i=1}^m(\overline x - x_i)^2},\overline x = \frac 1m \sum\limits_{i=1}^m x_i \]其中 \(\sigma\) 为均方差,\(\bar{x}\) 为各组数据和的平均值,\(x_i\) 为第 \(i\) 组数据的数值和。
【数据规模】
对于 \(40\%\) 的数据,保证有 \(m \le n \le 10\),\(2 \le m \le 6\)
对于 \(100\%\) 的数据,保证有 \(m \le n \le 20\)。
凭借数学直觉,我们发现,每组数越接近,答案越优
证明来源于WJiannan 的博客
看看原式:$$\sigma=\sqrt{\sum_{i=1}n (x_i-\bar{x})2 \over n}\quad\bar{x}={\sum_{i=1}^n\ x_i \over n}$$
同时平方:$$n\sigma2=\sum_{i=1}n\ (x_i-\bar{x})^2$$
拆开算式:\(n\sigma^2=\sum_{i=1}^n x_i^2-2\bar{x}\sum_{i=1}^{n}x_i + \sum_{i=1}^{n}\bar{x}^2\)
我们知道 \(-2\bar{x}\sum_{i=1}^{n}x_i + \sum_{i=1}^{n}\bar{x}^2\) 都是定值,
也可以推测出当 \(\sum_{i=1}^{n}x_i\) 为定值,每个 \(x\) 尽量接近时,\(\sum_{i=1}^n x_i^2\) 最小。
证毕!
于是一个显而易见的贪心出现了,即每次把数字扔到最小的一个组内。
但是用脚造数据都能hack它,欸,这个时候
"无所谓,随机化会出手"
\(Code:\)
#include<algorithm>
#include<iostream>
#include<cstdio>
#include<random>
#include<queue>
#include<cmath>
using namespace std;
int n,m;
int a[30];
double ans=1e11;
double ba=0;
double work()
{
double res=0;
priority_queue<int,vector<int>,greater<int> > q;
//使用优先队列,记录每组中加和
for(int i=1;i<=m;i++) q.push(0);
for(int i=1;i<=n;i++)
{
int tmp=a[i]+q.top();
q.pop();q.push(tmp);
//把新数扔进最小的一堆
}
while(!q.empty())
{
//计算答案
int tmp=q.top();q.pop();
res+=(tmp-ba)*(tmp-ba);
}
return sqrt(res/m);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) {scanf("%d",&a[i]);ba+=a[i];}
ba/=m;//计算平均数
mt19937 r(time(0));
for(int tm=1;tm<=500000;tm++)
{
shuffle(a+1,a+1+n,r);//打乱
ans=min(ans,work());//统计答案
}
printf("%.2lf",ans);
return 0;
}
练习题
写在最后
随机化最终要的不是\(luck\)(运气),而是\(pluck\)(勇气),想不出来正解时,一个合理的随机化往往比暴力有更优的效果
参考:
https://blog.csdn.net/seacean2000/article/details/53455665
https://blog.csdn.net/weixin_46838605/article/details/124943782
https://www.luogu.com.cn/blog/wucstdio/solution-p1337
https://99nl.blog.luogu.org/guan-yu-mu-ni-tui-huo-di-xue-xi-bi-ji
https://steaunk.blog.luogu.org/solution-p2503
标签:double,sum,随机化,算法,邪术,solve,include From: https://www.cnblogs.com/Lkkaknoi/p/17118490.html