基于图搜索的路径规划
配置空间
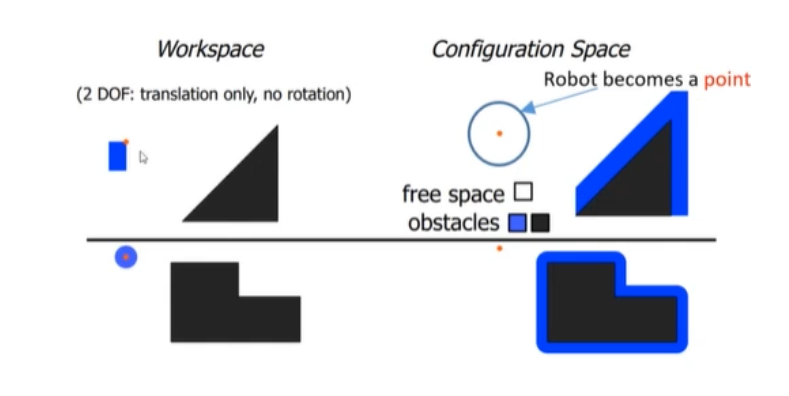
维度等于机器人的自由度,可以理解为一个点可以表示一个机器人的位姿。例如小车4自由度(x,y,z,θ)。在配置空间中,机器人表示为点。
在配置空间做规划
在3维空间中,要做碰撞检测,很麻烦。所以在配置空间中做规划,要对障碍物按照机器人的尺寸做膨胀,机器人看成一个点。
基于图搜索的算法框架

关键问题
如果一个结点被弹出容器,就不再会被加入到容器中
BFS使用的容器是队列,DFS使用的是栈。在边的权重都为1的情况下,BFS能保证路径最短,所以搜索算法是基于BFS的
启发
启发是一种对离目标点有多近的猜测(欧式距离,曼哈顿距离)
Dijkstra

与BFS相比,Dijkstra从容器中弹出的规则不同。Dijkstra弹出的是从起点到某点的走过的距离最短的点。也就是说,容器不再使用队列,而是优先队列,弹出的总是走过路径最短的点。
优点:完备的,能保证最优解
缺点:没有启发,就是暴力搜
A*
Dijkstra + 启发(预测的从该节点到终点的距离)
Accumulated cost: 从起点到当前节点cost的累加

Heuristic: 启发

相比于Dijkstra,A*的容器对元素的排序依赖的是(走过的路径的距离+启发距离)
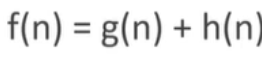

当启发距离小于真实距离的时候(admissble),A*能找到最优解。
欧式距离→ always
曼哈顿距离→depends(当机器人不能对角运动时)
L∞ norm→always
0→always
技巧
对于这些启发函数,h(n) ≤ h(n) 是满足的,但是在h(n)和h(n)之间有很大的gap,导致搜索过程存在浪费
Best Heuristic: 使用Diagonal Heuristic

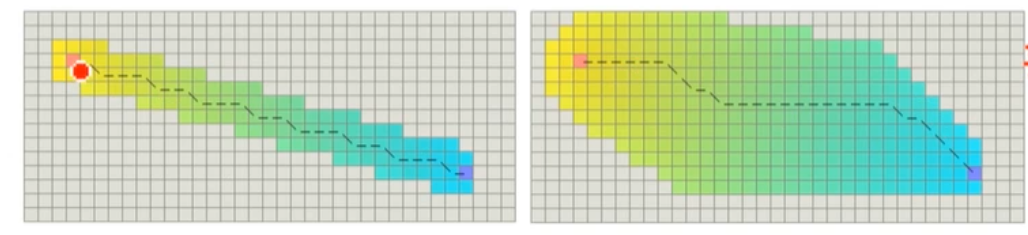
Breaker: 打破两个节点的f(n)相等的情况(对称性)
1.将h微小放大
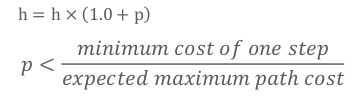

2.Tie Breaker: 对于相同f的节点有倾向性的选择一条路径
- f 相同比较 h
- 每个节点加一个随机值
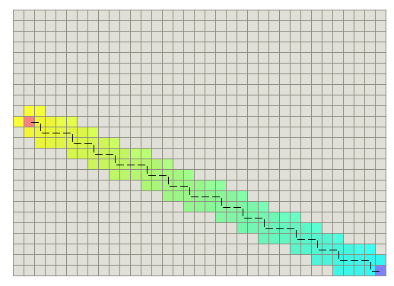
- 在 h 上加上 cross (当前节点距离起点和终点连线的偏移量)
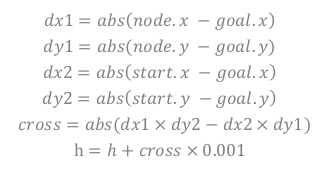
Jump Point Search
核心思想
找到图中的对称性,并打破对称性
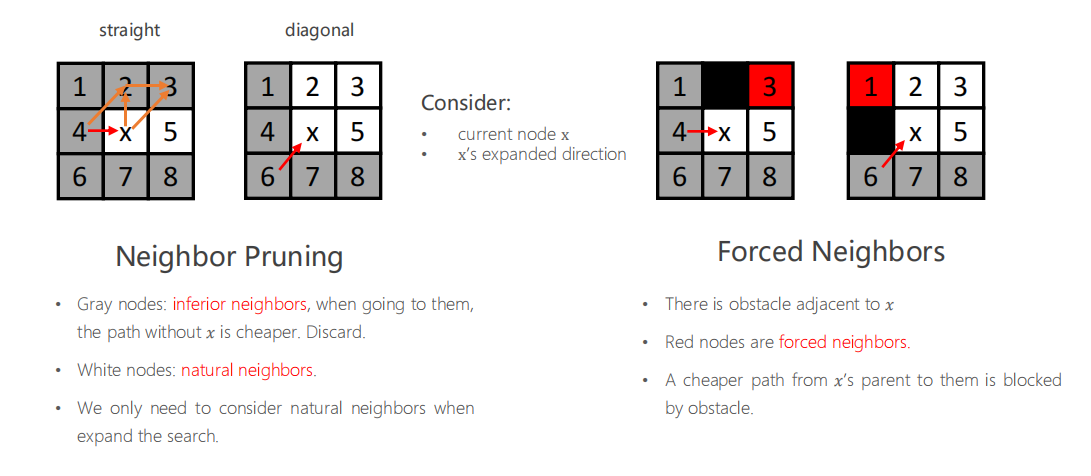
Look Ahead Rules
- 在周围没有障碍物的时候,对于当前的节点x,如果将要扩展的节点能够从他的父亲节点到达并且path的长度小于等于经过x的path长度,那么就没必要扩展。例如当前节点为x,父节点为4,对于2节点,4→2可以直接到达并且path长度小于4→x→2,那么2就没必要从4扩展。
- 当存在障碍物时,劣性的节点(不需要考察的节点)可能会转化为Forced Neighbor(需要考察的节点)。例如原本节点3不需要从x拓展,但是由于存在障碍物,从节点4(x的父节点)到节点3的最优路径不复存在,因此节点x需要考察节点3。
Jumping Rules
- 直线跳跃规则:从节点x沿着直线跳跃,直到节点y(关键节点),节点y有一个Forced Neighbor(节点z), 节点x到节点z没有比经过节点y更优的路径。
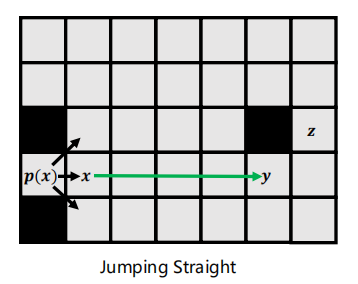
- 对角跳跃规则:当节点进行水平和垂直跳跃失败(遇到障碍物或者到达地图边界)后,进行对角跳跃,直到节点y(关键节点),y的下一个节点z有一个Forced Neighbor。同时节点x也有一个Forced Neighbor。
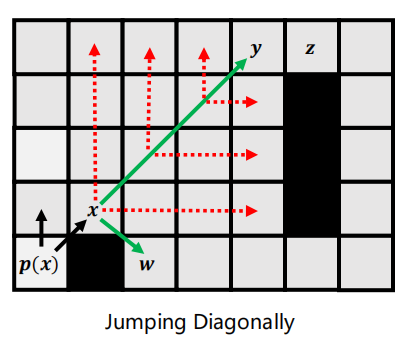

Jump Point Search
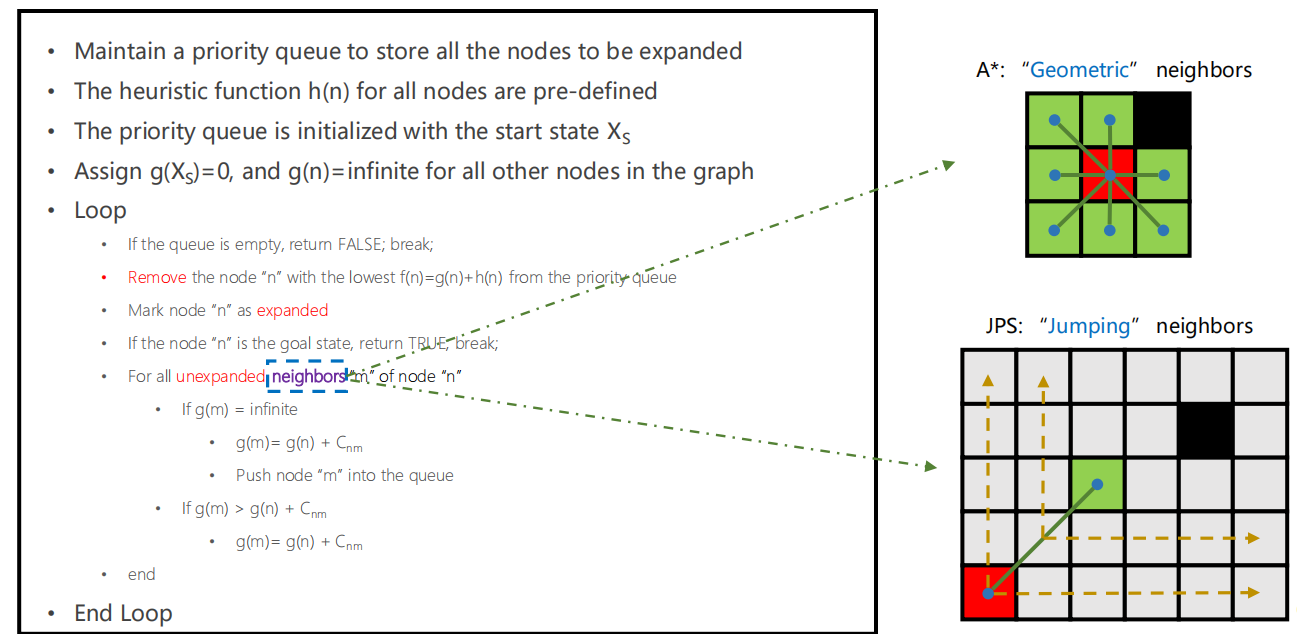
JPS与A几乎一模一样,不同点在于如何找当前节点的neighbors,对于A 就是除去障碍物的上下左右以及对角方向,JPS则是根据规则找到后继节点。
标签:障碍物,基于,路径,距离,Dijkstra,搜索,节点,启发 From: https://www.cnblogs.com/chenjq12/p/17111032.html