题目描述
给定一棵树,树中包含 \(n\) 个结点(编号\(1\)~\(n\))和 \(n-1\) 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
解题思路
\(\qquad\)首先因为是树所以有这样的一个性质:树上两点之间有且仅有一条路径,路径\((x,y)\)可以拆分成两条路径 \((x,r)\) 和 \((r,y)\),其中 \(r\) 表示 \(LCA(x, y)\)。
\(\qquad\)所以我们可以得到一个思路:枚举断点 \(r\),状态 \(dist[r]\) 表示 \(r\) 的子树中,与 \(r\) 距离最远的点的距离。对于 \(r\) 的所有子节点 \(x_1, x_2, x_3,......x_k\),有
\[\Large dist[r] = \max_{1\le i\le k}\{ dist[x_i] + w(r,x_i)\} \]\(\qquad\) 然后再定义 \(f[x]\) 为以 \(x\) 为断点的最长链,那么树的直径就是
\[\Large \max_{1\le x\le n}\{f[x]\} \]求\(f\)的过程如下图所示
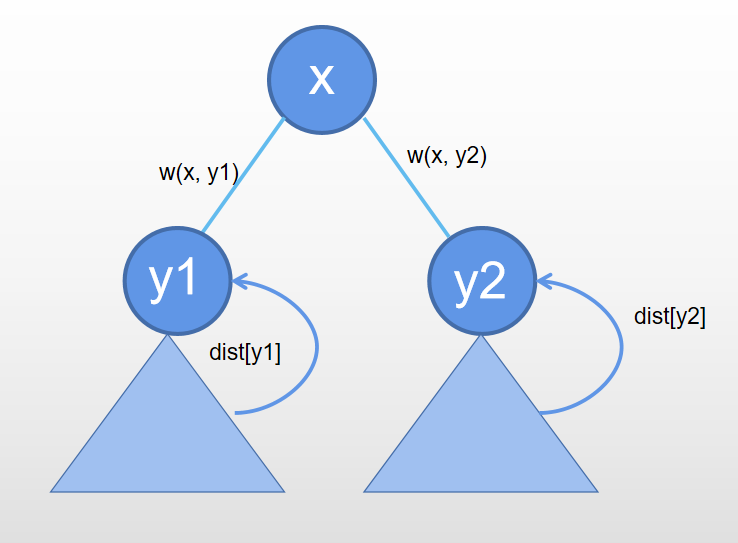
对于 \(x\) 的任意两个子节点 \(y_i\) 和 \(y_j\),\(f[x]\) 可以分成下面四个部分的和
\(\qquad 1.\) 从 \(y_i\) 到 \(y_i\) 的子树的最大距离
\(\qquad 2.\) 从 \(y_i\) 到 \(x\) 的距离
\(\qquad 3.\) 从 \(x\) 到 \(y_j\) 的距离
\(\qquad 4.\) 从 \(y_j\) 到 \(y_j\) 子树的最大距离
因此$$\large f[x] = \max_{1\le j<i\le k}{{dist[y_i] + dist[y_j] + w(x,y_i) + w(x,y_j) }}$$
然后就OK了
优化
如果我么顺序枚举,那么在将要枚举到 \(i\) 的时候,对于每个已经枚举过的节点 \(j < i\) 我们都可以保存到从 \(x\) 出发走向以 \(y_j\) 为根的子树最大距离,这个距离也就是
\[\large \max_{1\le j < i}\{dist[y_j] + w(x,y_j)\} \]所以我们可以一边枚举一边用\(dist[x] + dist[y_i] + w(x, y_i)\) 更新 \(f[x]\), 一边用\(dist[y_i] + w(x, y_i)\) 更新 $ dist[x]$。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010, M = N << 1;
int h[N], e[M], w[M], ne[M], idx = 1;
bool st[N]; int n, dist[M], res = -0x3f3f3f;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dp(int x)
{
st[x] = true;
for (int i = h[x]; ~i; i = ne[i])
{
int j = e[i];
if (st[j]) continue ;
dp(j);
res = max(res, dist[x] + dist[j] + w[i]);
dist[x] = max(dist[x], dist[j] + w[i]);
}
res = max(res, dist[x]);
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d", &n);
while (n -- )
{
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
add(u, v, w), add(v, u, w);
}
dp(1);
printf("%d\n", res);
return 0;
}