标签：matrix int self 矩阵 6292 差分 dp sumRegion DP

304. 二维区域和检索 - 矩阵不可变

Description

Difficulty: 中等

Related Topics: 设计, 数组, 矩阵, 前缀和

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

示例 1：

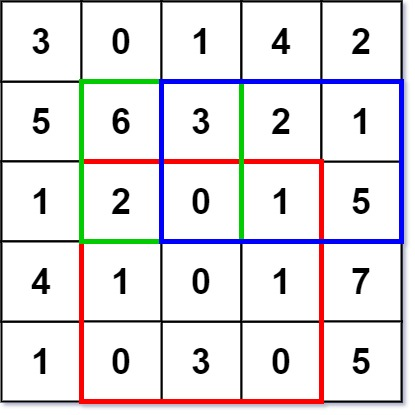
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -10⁵ <= matrix[i][j] <= 10⁵
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 10⁴ 次 sumRegion 方法

Solution

二维前缀和模版题。
Language: Python3

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        if not matrix or not matrix[0]:
            self.dp = None
        m, n = len(matrix), len(matrix[0])
        self.dp = [[0] * (n + 1) for _ in range(m + 1)]
        for i in range(m):
            for j in range(n):
                self.dp[i + 1][j + 1] = self.dp[i][j + 1] + self.dp[i + 1][j] - self.dp[i][j] + matrix[i][j]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        if not self.dp: return 0
        return self.dp[row2 + 1][col2 + 1] - self.dp[row2 + 1][col1] - self.dp[row1][col2 + 1] + self.dp[row1][col1]




# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

6292. 子矩阵元素加 1

Description

Difficulty: 中等

Related Topics:

给你一个正整数 n ，表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ，矩阵中填满了 0 。

另给你一个二维整数数组 query 。针对每个查询 query[i] = [row1_i, col1_i, row2_i, col2_i] ，请你执行下述操作：

• 找出 左上角 为 (row1_i, col1_i) 且 右下角 为 (row2_i, col2_i) 的子矩阵，将子矩阵中的 每个元素 加 1 。也就是给所有满足 row1_i <= x <= row2_i 和 col1_i <= y <= col2_i 的 mat[x][y] 加 1 。

返回执行完所有操作后得到的矩阵 mat 。

示例 1：

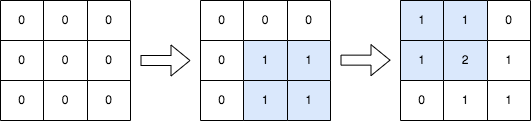
输入：n = 3, queries = [[1,1,2,2],[0,0,1,1]]
输出：[[1,1,0],[1,2,1],[0,1,1]]
解释：上图所展示的分别是：初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。
- 第一个操作：将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。 
- 第二个操作：将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。 

示例 2：

输入：n = 2, queries = [[0,0,1,1]]
输出：[[1,1],[1,1]]
解释：上图所展示的分别是：初始矩阵、执行完第一个操作后的矩阵。 
- 第一个操作：将矩阵中的每个元素加 1 。

提示：

• 1 <= n <= 500
• 1 <= queries.length <= 10⁴
• 0 <= row1_i <= row2_i < n
• 0 <= col1_i <= col2_i < n

Solution

二维差分前缀和模版题。
Language: Python3

class Solution:
    def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:
        mat = [[0] * n for _ in range(n)]
        for x1, y1, x2, y2 in queries:
            for i in range(x1 ,x2 + 1):
                for j in range(y1, y2 + 1):
                    mat[i][j] += 1
        return mat

标签：matrix,int,self,矩阵,6292,差分,dp,sumRegion,DP
From： https://www.cnblogs.com/hyserendipity/p/17053842.html