线段树合并
温馨提示:学习此内容之前,确保你会动态开点
如果不太会,可以自行搜搜。
什么是线段树合并(如果会了可以自行跳过)
总的来说,就是把两颗形状一样的线段树合并在一起(特别的,在我们动态开点中,不需要保证形状完全相等(因为有些点没开,有些点开了))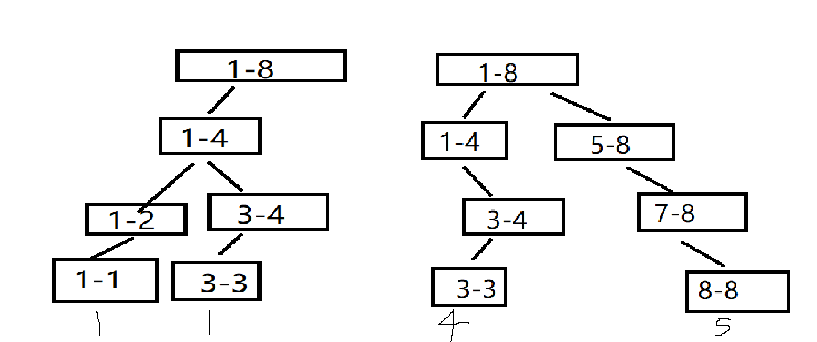
如上图两个线段树,我们把上面两个线段树合并起来,规则如下:
线段树合并规则
1.规定C线段树为A线段树和B线段树合并起来的线段树
2.每个C线段树的非叶子节点根据C本身pushup算
3.如果C中有一个区间A有B没有(或者B有A没有),就直接C的lson/rson指向A/B的lson/rson
4.如果A线段树和B线段树搜到的这个区间,A和B中都有,就向下搜子树
5.如果搜到叶节点,两树都有,那么就直接c[u].val=a[u].val+b[u].val;
不理解?那就模拟一下好了
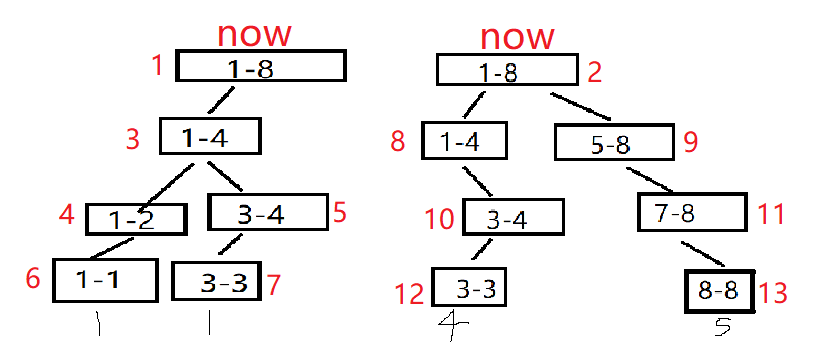
温馨提示:红色代表的是线段树中这个区间的下标,因为是动态开点所以连续,所以下标是连续的,叶节点下方的数字代表的是val
(在这里我们把所有线段树放在一个数组里面,这无所谓,ls/rs指向自己儿子就行)
假设C树的根节点下标为14
最开始在根节点

都有1-4这个区间所以向下搜
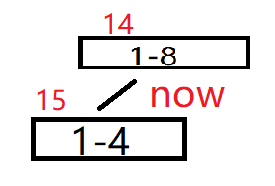
然后搜[1-2],只有A中有这个区间,B中没有,所以直接将c[u].lson=a[u].lson(1-2相当于a和c的共享儿子,直接接到c的1-4上)
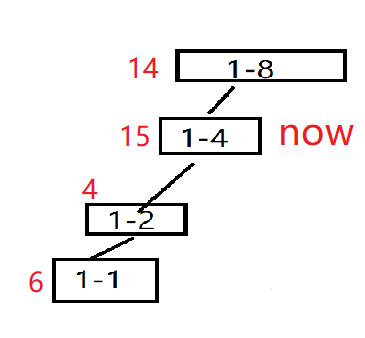
然后搜[3-4],发现两个树都有[3-4],新开一个点,就继续向下搜;
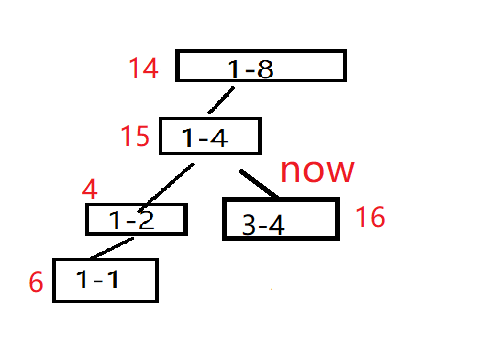
然后搜[3-3],发现是叶子节点,那么就合并两个直接c[u].val=a[u].val+b[u].val;
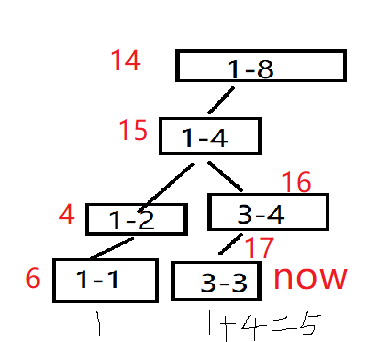
然后pushup回溯,就将c线段树普通回溯(下面展示的是求区间和的回溯)
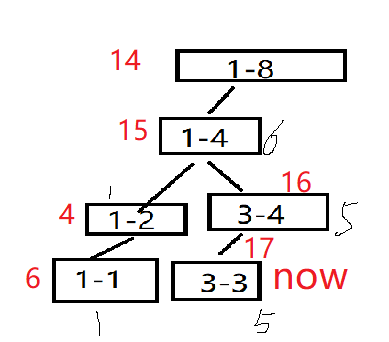
剩下的线段树合并也是一样的操作,就不详细描述了,直接放结果(其实就一步因为a没有右子树)
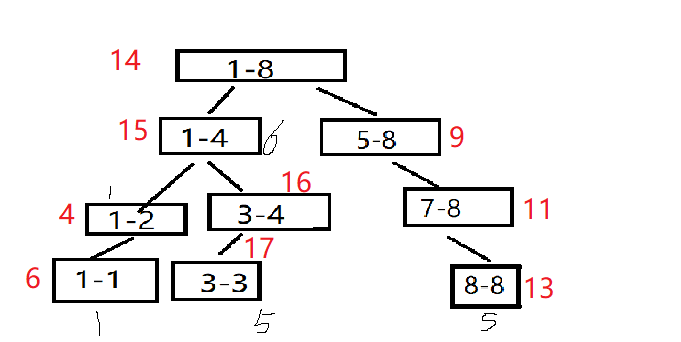
那么在这道题目中线段树合并有什么关系,为什么说这个题是线段树合并模板?
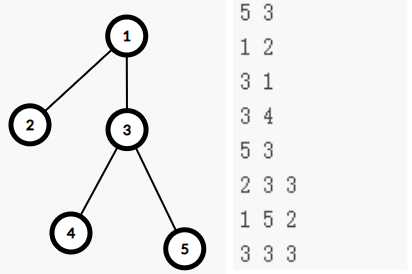
这是题目的样例(假设1是根)
我们分别要在2-3这个路径上放3,1-5这个路径上放2,3-3这个路径上放3
敲重点:
每个节点修一个线段树,单点就是救济粮种类,这个节点被发了救济粮就在线段树单点修改,叶子节点的区间[a,a]代表a号救济粮的个数,普通区间[a,b]就记录a-b区间内最大救济粮个数和种类号(动态开点所以不会爆炸)
pushup的代码如下(挺好理解的):
`
void pushup(int u){
if(tree[tree[u].ls].max_num>tree[tree[u].rs].max_num){
tree[u].max_num=tree[tree[u].ls].max_num;
tree[u].max_id=tree[tree[u].ls].max_id;
}else if(tree[tree[u].ls].max_num<tree[tree[u].rs].max_num){
tree[u].max_num=tree[tree[u].rs].max_num;
tree[u].max_id=tree[tree[u].rs].max_id;
}else if(tree[tree[u].ls].max_id<tree[tree[u].rs].max_id){
tree[u].max_num=tree[tree[u].ls].max_num;
tree[u].max_id=tree[tree[u].ls].max_id;
}else{
tree[u].max_num=tree[tree[u].rs].max_num;
tree[u].max_id=tree[tree[u].rs].max_id;
}
}`
这个地方我最开始理解了很久
我们可以直接遍历,然后每个点加一次,但时间复杂度是O(nm) 这是不能接受的
我们考虑有两种方法:
1.树链剖分(作者会但考场写挂了)
2.树上前缀和/差分
首先不要被这个名词吓住,其实只要你会了前缀和/分就该会树上前缀和/差分
在这里作者以差分为例子(因为这道题用差分)
我们先来想想普通差分是什么
这是一个数组a=[1,1,4,5,1,4]
我们区间修改要O(n)
差分就是cf[i]=a[i]-a[i-1];得到cf=[1,0,3,1,-4,3]
这样我们区间修改就只用O(2);
还原这个数组也就是求差分序列的前缀和
那么差分树是什么意思呢?
先随便画一个树:
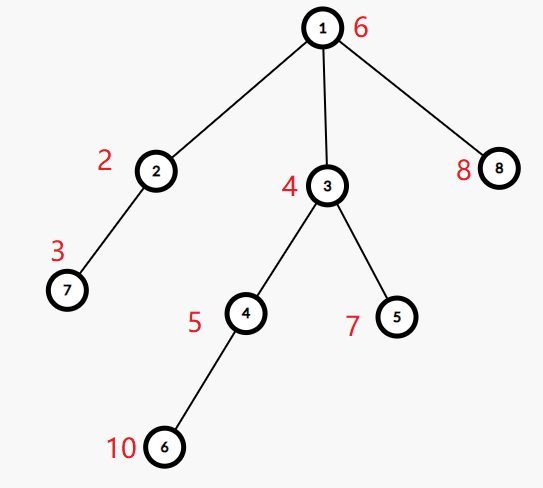
他的差分树是
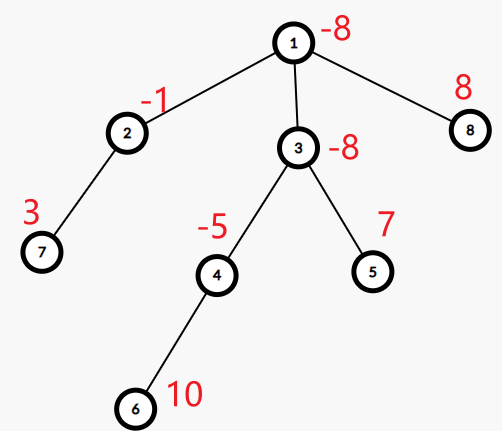
观众可以先自行观察一下这个差分树怎么来的
obviously,差分树上的值是原本树上的值减去他所有子树的值
还原就直接把这个节点和以他为根的子树全部加起来,dfs然后再回溯的时候加可以在O(n)将差分树还原成原本树
那么现在在将a-b路径发救济粮就可以直接在差分树上的v[a]++;v[b]++;v[lca(a,b)]--,v[fa(lca(a,b))]--;读者可以自行推导模拟一下为什么这样是正确的;
``
到最后我们的线段树合并就派上用场了,我们在算原树的时候就要全部加起来,这个时候就需要用到线段树合并;
下面是找lca(我用的是倍增)
`
int lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
while(dep[x]>dep[y]){
x=fa[x][lg2(dep[x]-dep[y])];
//cout<<"a"<<lg2(dep[x]-dep[y]);
}
if(x==y) return x;
for(int i=19;i>=0;i--){
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
}
return fa[x][0];
}`
下面是我们在x-y路径发w救济粮的代码
`
void add_tree(int x,int y,int w){
int lc=lca(x,y);
add_on(root[x],1,N,w,1);
add_on(root[y],1,N,w,1);
add_on(root[lc],1,N,w,-1);
add_on(root[fa[lc][0]],1,N,w,-1);
}`
下面是在线段树上某个点(某种救济粮)进行改变的过程
`
int merge(int l,int r,int x,int y){
if(x==0) return y;
if(y==0) return x;
if(l==r){
tree[x].val+=tree[y].val;
tree[x].max_num=tree[x].val;
return x;
}
int mid=(l+r)>>1;
tree[x].ls=merge(l,mid,tree[x].ls,tree[y].ls);
tree[x].rs=merge(mid+1,r,tree[x].rs,tree[y].rs);
pushup(x);
return x;
}`
下面是操作完后通过差分序列算原本序列的dfs过程
`
void dfs2(int x){
for(int i=head[x];i;i=edge[i].next){
int y=edge[i].to;
if(y==fa[x][0]) continue;
dfs2(y);
merge(1,N,root[x],root[y]);
}
} `
下面是线段树合并(差分相加得到原本)
`
int merge(int l,int r,int x,int y){
if(x==0) return y;
if(y==0) return x;
if(l==r){
tree[x].val+=tree[y].val;
tree[x].max_num=tree[x].val;
return x;
}
int mid=(l+r)>>1;
tree[x].ls=merge(l,mid,tree[x].ls,tree[y].ls);
tree[x].rs=merge(mid+1,r,tree[x].rs,tree[y].rs);
pushup(x);
return x;
}`
总代码:
`
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m,tot=0,head[N],x,y,w,fa[N][20],dep[N],s;
int root[N];
struct node{
int next,to;
}edge[2*N];
struct node1{
int ls,rs,val;
int max_id,max_num;
}tree[100*N];
void pushup(int u){
if(tree[tree[u].ls].max_num>tree[tree[u].rs].max_num){
tree[u].max_num=tree[tree[u].ls].max_num;
tree[u].max_id=tree[tree[u].ls].max_id;
}else if(tree[tree[u].ls].max_num<tree[tree[u].rs].max_num){
tree[u].max_num=tree[tree[u].rs].max_num;
tree[u].max_id=tree[tree[u].rs].max_id;
}else if(tree[tree[u].ls].max_id<tree[tree[u].rs].max_id){
tree[u].max_num=tree[tree[u].ls].max_num;
tree[u].max_id=tree[tree[u].ls].max_id;
}else{
tree[u].max_num=tree[tree[u].rs].max_num;
tree[u].max_id=tree[tree[u].rs].max_id;
}
}
void add_on(int u,int l,int r,int w,int val){
// cout<<u<<endl;
//if(u==0) u=++tot;
if(l==r){
tree[u].val+=val;
tree[u].max_id=w;
tree[u].max_num=tree[u].val;
return ;
}
int mid=(l+r)>>1;
if(w<=mid){
if(tree[u].ls==0) tree[u].ls=++tot;
add_on(tree[u].ls,l,mid,w,val);
}else{
if(tree[u].rs==0) tree[u].rs=++tot;
add_on(tree[u].rs,mid+1,r,w,val);
}
pushup(u);
}
int lg2(int x){
int a=1,ans=0;
while(x>a){
a*=2;
ans++;
}
if(a==x)return ans;
else return ans-1;
}
void add(int x,int y){
tot++;
edge[tot].next=head[x];
edge[tot].to=y;
head[x]=tot;
}
void input(){
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
}
void dfs1(int x){
dep[x]=dep[fa[x][0]]+1;
for(int i=0;fa[x][i];i++)fa[x][i+1]=fa[fa[x][i]][i];
for(int i=head[x];i;i=edge[i].next){
int y=edge[i].to;
if(y==fa[x][0])continue;
fa[y][0]=x;
dfs1(y);
}
}
int lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
while(dep[x]>dep[y]){
x=fa[x][lg2(dep[x]-dep[y])];
}
if(x==y) return x;
for(int i=19;i>=0;i--){
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
}
return fa[x][0];
}
void add_tree(int x,int y,int w){
int lc=lca(x,y);
add_on(root[x],1,N,w,1);
add_on(root[y],1,N,w,1);
add_on(root[lc],1,N,w,-1);
add_on(root[fa[lc][0]],1,N,w,-1);
}
int merge(int l,int r,int x,int y){
if(x==0) return y;
if(y==0) return x;
if(l==r){
tree[x].val+=tree[y].val;
tree[x].max_num=tree[x].val;
return x;
}
int mid=(l+r)>>1;
tree[x].ls=merge(l,mid,tree[x].ls,tree[y].ls);
tree[x].rs=merge(mid+1,r,tree[x].rs,tree[y].rs);
pushup(x);
return x;
}
void dfs2(int x){
for(int i=head[x];i;i=edge[i].next){
int y=edge[i].to;
if(y==fa[x][0]) continue;
dfs2(y);
merge(1,N,root[x],root[y]);
}
}
void op(){
tot=0;
for(int i=1;i<=n;i++){
root[i]=++tot;
}
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&w);
add_tree(x,y,w);
}
dfs2(1);
}
int main(){
input();
dfs1(1);
op();
for(int i=1;i<=n;i++) cout<<tree[i].max_id<<endl;
return 0;
}`