【带你读论文】向量表征经典之DeepWalk

标签：DeepWalk 随机 Embedding 游走 表征 节点 向量

摘要：详细讲解DeepWalk，通过随机游走的方式对网络化数据做一个表示学习，它是图神经网络的开山之作，借鉴了Word2vec的思想。

本文分享自华为云社区《[论文阅读] (25) 向量表征经典之DeepWalk：从Word2vec到DeepWalk，再到Asm2vec和Log2vec》，作者：eastmount 。

一.图神经网络发展历程

在介绍向量表征之前，作者先结合清华大学唐杰老师的分享，带大家看看图神经网络的发展历程，这其中也见证了向量表征的发展历程，包括从Word2vec到Deepwalk发展的缘由。

图神经网络的发展历程如下图所示：

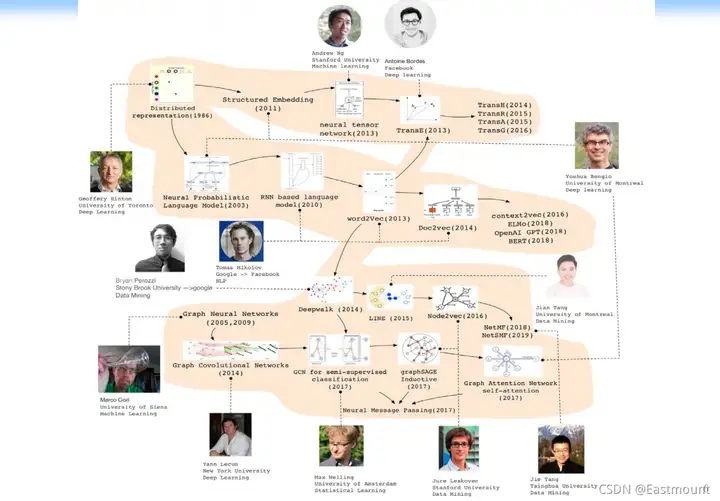
（1）Hinton早期（1986年）

图神经网络最早也不是这样的，从最早期 Hinton 做了相关的思路，并给出了很多的ideas，他说“一个样本可以分类成不同的representation，换句话，一个样本我们不应该去关注它的分类结果是什么，而更应该关注它的representation，并且它有很多不同的representation，每个表达的意思可能不同” ，distributed representation 后接着产生了很多相关的研究。

（2）扩展（Bengio到Word2Vec）

Andrew Ng 将它扩展到网络结构上（结构化数据），另一个图灵奖获得者Yoshua Bengio将它拓展到了自然语言处理上，即NLP领域如何做distributed representation，起初你可能是对一个样本representation，但对自然语言处理来讲，它是sequence，需要表示sequence，并且单词之间的依赖关系如何表示，因此2003年Bengio提出了 Nerual Probabilistic Language Model，这也是他获得图灵奖的一个重要工作。其思路是：每个单词都有一个或多个表示，我就把sequence两个单词之间的关联关系也考虑进去。

• Yoshua Bengio, Rejean Ducharme, Pascal Vincent, and Christian Jauvin. A neural probabilistic language model. Journal of Machine Learning Research (JMLR), 3:1137–1155, 2003.
• 原文地址：https://www.jmlr.org/papers/volume3/bengio03a/bengio03a.pdf

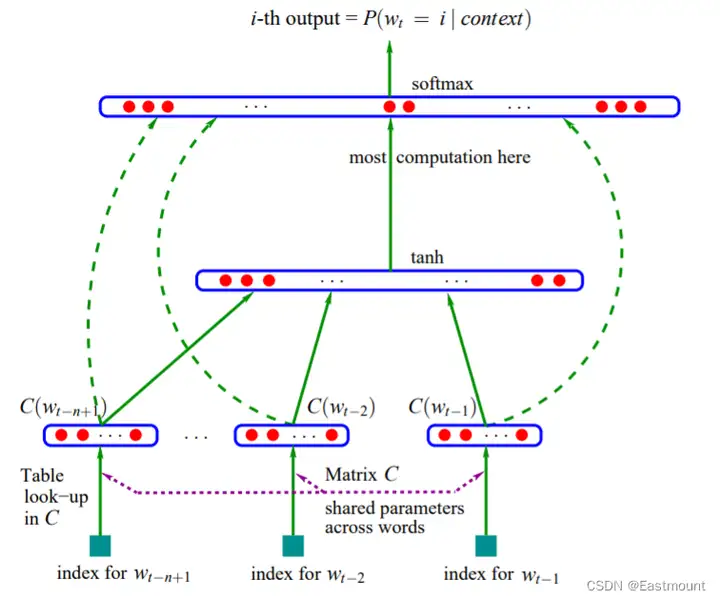
但是，当时做出来后由于其计算复杂度比较高，很多人无法fellow。直到谷歌2013年提出 Word2Vec，基本上做出来一个场景化算法，之后就爆发了，包括将其扩展到paragraph、文档（Doc2Vec）。补充一句，Word2Vec是非常经典的工作或应用，包括我们安全领域也有相关扩展，比如二进制、审计日志、恶意代码分析的Asm2Vec、Log2Vec、Token2Vec等等。

• Efficient Estimation of Word Representations in Vector Space
• 原文地址：https://arxiv.org/abs/1301.3781v3

(3) 网络化数据时期（Deepwalk）

此后，有人将其扩展到网络化的数据上，2014年Bryan做了 Deepwalk 工作。其原理非常建立，即：原来大家都在自然语言处理或抽象的机器学习样本空间上做，那能不能针对网络化的数据，将网络化数据转换成一个类似于自然语言处理的sequence，因为网络非常复杂，网络也能表示成一个邻接矩阵，但严格意义上没有上下左右概念，只有我们俩的距离是多少，而且周围的点可多可少。如果这时候在网络上直接做很难，那怎么办呢？

通过 随机游走 从一个节点随机到另一个节点，此时就变成了一个序列Sequence，并且和NLP问题很像，接下来就能处理了。

• 原文地址：https://dl.acm.org/doi/10.1145/2623330.2623732

随后又有了LINE（2015）、Node2Vec（2016）、NetMF（2018）、NetSMF（2019）等工作，它们扩展到社交网络领域。唐老师们的工作也给了证明，这些网络本质上是一个Model。

(4) 图卷积神经网络（GCN）时期

2005年，Marco Gori 实现了 Graph Neural Networks。2014年，Yann Lecun 提出了图卷积神经网络 Graph Convolutional Networks。2017年，Max Welling将图卷积神经网络和图数据结合在一起，完成了 GCN for semi-supervised classification，这篇文章引起了很大关注。还有很多不做卷积工作，因此有很多Graph Neural Networks和Neural Message Passing（一个节点的分布传播过去）的工作。Jure针对节点和Transductive Learning又完成了 Node2vec 和 grahpSAGE 两个经典工作。唐老师他们最近也做了一些工作，包括 Graph Attention Network。

GraphSAGE 是 2017 年提出的一种图神经网络算法，解决了 GCN 网络的局限性: GCN 训练时需要用到整个图的邻接矩阵，依赖于具体的图结构，一般只能用在直推式学习 Transductive Learning。GraphSAGE 使用多层聚合函数，每一层聚合函数会将节点及其邻居的信息聚合在一起得到下一层的特征向量，GraphSAGE 采用了节点的邻域信息，不依赖于全局的图结构。

• Hamilton, Will, Zhitao Ying, and Jure Leskovec. “Inductive representation learning on large graphs.” Advances in neural information processing systems. 2017.
• 原文地址：https://proceedings.neurips.cc/paper/2017/file/5dd9db5e033da9c6fb5ba83c7a7ebea9-Paper.pdf

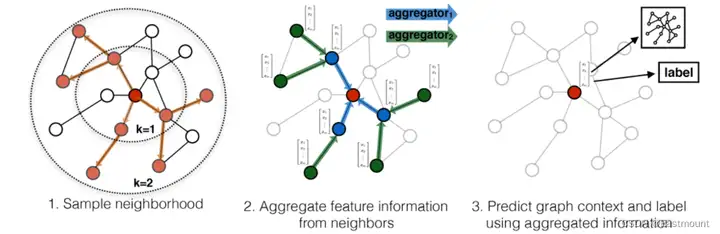
Data Mining over Networks

• DM tasks in networks:
  – Modeling individual behavior
  – Modeling group behavioral patterns
  – Reveal anomaly patterns
  – Deal with big scale

第一部分花费大量时间介绍了研究背景，接下来我们正式介绍这六个工作。

二.Word2vec：NLP经典工作（谷歌）

（详见前文）

Word2vec是一个用于生成词向量(word vectors)并预测相似词汇的高效预测框架，Word2vec是Google公司在2013年开发。

• Tomás Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean. Efficient Estimation of Word Representations in Vector Space. ICLR, 2013.

三.Doc2vec

（详见前文）

在Word2Vec方法的基础上，谷歌两位大佬Quoc Le和Tomas Mikolov又给出了Doc2Vec的训练方法，也被称为Paragraph Vector，其目标是将文档向量化。

• Quoc V. Le, Tomás Mikolov. Distributed Representations of Sentences and Documents. ICML, 2014: 1188-1196.

四.DeepWalk：网络化数据经典工作（KDD2014）

(一).论文阅读

原文标题：Deepwalk: Online learning of social representations
原文作者：Perozzi B, Al-Rfou R, Skiena S
原文链接：https://dl.acm.org/doi/abs/10.1145/2623330.2623732
发表会议：2014 KDD，Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining
参考资料：强推B站同济子豪兄 - https://www.bilibili.com/video/BV1o94y197vf

DeepWalk是图嵌入（Graph Embedding）的开山之作，于2014年被Bryan Perozzi等提出，旨在将图中的每一个节点编码为一个D维向量，为后续节点分类等下游任务提供支撑。DeepWalk通过随机游走算法从一个节点随机到另一个节点，从而将网络化数据转换成一个序列（Sequence），再利用类似于NLP的方法处理。DeepWalk将图当作语言，节点当作单词来生成Embedding。

1.摘要

本文提出了DeepWalk，一种新颖的（novel）用于学习网络节点的隐式表征（latent representations）的方法。这些隐式表征能够把节点在图中的连接关系进行编码，编码为一个稠密低维连续的向量空间（vector space），再通过该向量很容易地完成后续的统计机器学习分类。DeepWalk对现有的语言模型和无监督特征学习（或深度学习）的最新进展进行了概括，将原本用于NLP领域对文本或单词序列进行建模的方法（如Word2Vec）用至图中，对节点进行嵌入。

DeepWalk使用有截断的 随机游走（random walks） 序列去学习局部信息的隐层表示，并将随机游走序列当作是句子。我们演示了DeepWalk在社交网络的一些多类别网络分类任务上的隐式表示，比如BlogCatalog（博客）、Flickr（图片）和YouTube（视频）。实验结果表明DeepWalk的表现优于现有的同类（基线）算法，后者拥有一个网络的全局视图，特别是在信息缺失（标注稀疏）的场景下。当标记数据稀疏（sparse）时，DeepWalk的表示可以提供比竞争方法高出10%的F1值。在一些实验中，DeepWalk的表示优于所有基线方法，并且少使用60%的训练数据。

DeepWalk也是可扩展的（scalable）。它是一个在线学习算法，可以迭代有用的增量学习结果，并且是并行的。这些特性使得它可以适用于广泛的现实世界的应用中，如网络分类（network classification）和异常检测（anomaly detection）。

2.引言和贡献

由于引言至关重要，因此该部分会全文介绍，学习这些经典文章如何介绍背景、引出问题及本文的贡献及动机。

网络表示的稀疏性（sparsity）既是优点也是缺点。稀疏性使得设计有效的离散算法成为可能，但如果使用统计机器学习模型去分类或回归就会很困难。网络中的机器学习应用（如网络分类、内容推荐、异常检测和缺失链路预测）必须能够处理这种稀疏性，才能生存下来（或工作）。

在本文中，我们介绍了深度学习（无监督特征学习）技术 [3]，即Word2Vec，该技术在自然语言处理中已被证明是成功的，并首次将其引入到网络分析中。

• [3] Y. Bengio, A. Courville, and P. Vincent. Representation learning: A review and new perspectives. 2013.

我们提出了DeepWalk算法，通过建模一连串的随机游走序列来学习一个图的顶点的网络连接表示（social representations，即连接结构信息）。连接结构信息是捕获邻域相似性和社群成员信息的顶点的隐式特征。这些隐式表示编码连接关系成一个连续低维稠密的向量空间。DeepWalk是神经语言模型的推广，通过随机游走序列去类比一个个句子。神经语言模型（Word2Vec）已被证明在捕获人类语言的语义和句法结构上非常成功，甚至是逻辑类比问题中。

DeepWalk将一个图作为输入，并产生一个隐式表示（向量）作为输出。本文方法应用于经典的空手道网络数据集的结果如图1所示。图1(a)是由人工排版的，图1(b)显示了我们方法所生成的2维向量（输出）。除了原图中的节点都惊人的相似外，我们注意到在图1(b)中出现了线性可分的边界，图1(b)的聚类结果对应于输入图1(a)中模块最大化的集群（用顶点颜色显示）。

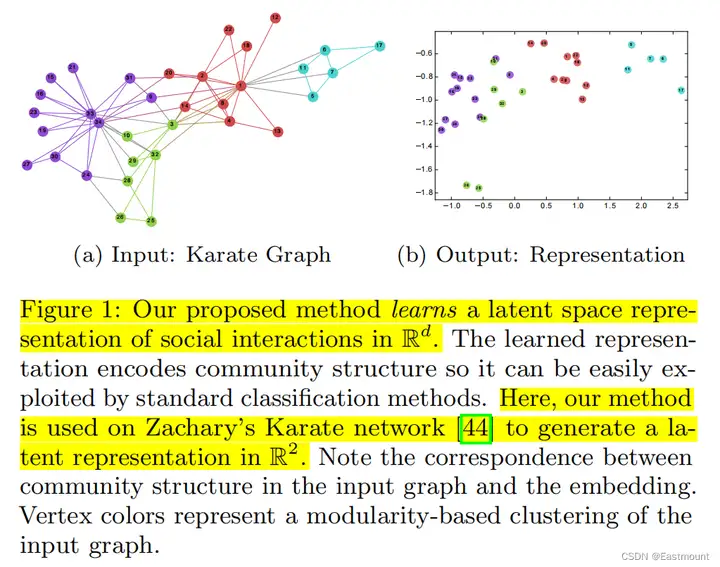
图1的补充内容：

(1) 图1(a)表示34个人组建的空手道俱乐部的无向图，连接表示两个人相互认识，后续分成了不同颜色的派系；图1(b)是经过DeepWalk编码后的D维向量（二维），它会将graph的每一个节点编码为一个D维向量（二维节点），绘制直角坐标系中会发现，原图中相近的节点嵌入后依然相近。该结果说明DeepWalk生成的Embedding隐式包含了graph中的社群、连接、结构信息。

(2) DeepWalk会将复杂的图转换成一个Embedding向量，然后下游任务再对该向量进行分类或聚类。此外，DeepWalk编码和嵌入属于无监督过程，没有用到任何的标记信息，只用到了网络的连接、结构、社群属性的信息，因为随机游走不会考虑节点的特征和类别信息，它只会采样图节点之间的顺序、结构信息。

(3) Karate Graph（空手道图）是经典的数据集，类似于机器学习中的鸢尾花数据集。

为了验证（demonstrate）DeepWalk在真实场景中的潜力，我们评估了它在大型异质图（heterogeneous graphs）中具有挑战性的多标签网络分类问题上的性能。在关系分类问题中，特征向量之间的链接违反了传统的独立同分布假设（i.i.d.）。解决这个问题的技术通常使用近似推理（approximate inference）技术来利用依赖信息以改进分类结果。我们跳出这些传统的方法（we distance ourselves），通过学习图的标签无关的表示来将每个节点表示为一个向量。我们的表示质量不受标记顶点选择的影响（无监督学习），因此它们可以在任务之间共享。

• 关系分类问题（relational classification）：在图中标注一些节点，用已有节点去预测未标注节点的类别，如攻击者识别。
• 独立同分布假设：在鸢尾花或MNIST图谱数据集中，每个样本（花）之间或数字之间是无关的，彼此互不影响，但它们都是鸢尾花或手写数字图像，因此叫独立同分布，适用于传统的机器学习。然而，在图中，比如标注已有的攻击者去预测未知的攻击者，图之间是存在联系的，因此既不独立也不一定满足同分布，没法直接用传统的LR、SVM、DT算法解决。

DeepWalk在创建连接维度方面优于其它的隐式表示方法，特别是在标记节点稀疏的情况下。我们的表示具有很强的性能，能够使用非常简单的线性分类器（如逻辑回归）完成相关实验。此外，我们的表示方法是通用的，并且可以与任何分类方法（包括传统的迭代推理方法）相结合。DeepWalk同时也是一个在线学习算法，并且能并行加速。

本文的贡献如下：

• 我们引入深度学习作为图嵌入的工具，以建立适用于统计机器学习建模且鲁棒的向量表示。DeepWalk能够通过随机游走序列学习图的结构规律。
• 我们在多个社交网络的多标签分类任务上评估了本文的表示方法。特别在标注稀疏的场景下，DeepWalk显著提高了分类的性能，Micro F1值提高了5%到10%。在某些情况下，即使减少了60%的训练数据，DeepWalk的表现也可以超过竞争算法。
• 我们通过并行加速将DeepWalk扩展到互联网级别的图（如YouTube）上来证明我们算法的可扩展性。此外，我们还进行了一些变种改进，通过构建streaming version所需的最小变化来生成图嵌入。

3.问题定义

首先需要解决节点分类问题。我们考虑将一个社交网络的成员划分为一个或多个类别的问题。

• G = (V,E)：V表示网络的节点，E表示连接关系。
• E ⊆ (V×V)：E可以表示成一个V行V列的邻接矩阵，表明第i个节点和第j个节点存在联系。
• G_L = (V,E,X,Y)：X表示特征（每个节点有S维特征），Y表示类别，|V|表示节点个数，|y|表示类别个数，G_L为被标注的社交网络。

在传统机器学习算法中，通常需要拟合一个映射H，它将X的元素映射到标签集y中。在本文的示例中，由于是图数据，因此需要利用图G结构中的依赖重要信息来获得优越的性能。在本文中，这种称为关系分类（relational classification）或集体分类（collective classification）问题。

• 传统关系分类解决方法：无向马尔科夫网络推理，通过迭代近似推理算法（如迭代分类算法、Gibbs采样、Label relaxation）计算标签给定网络结构的后验概率分布。
• 本文关系分类解决方法：提出一种新颖的方法来捕获网络拓扑信息。该方法不将标签和连接特征混合，而是通过随机游走序列来采样连接信息，即仅在Embedding中通过随机游走来编码连接信息，这是一种无监督的学习方法。

该方法的好处是将网络的连接结构信息（结构表征）和标签信息分开，从而避免误差累积（cascading errors）。此外，相同的表示方法（即图嵌入）可以用于各种网络相关的多分类问题。

本文的目标是学习到一个X_E矩阵，如下所示：比如将10个节点（|V|），每个节点压缩成128维度（d）的向量。其中，d可以是一个低维分布的向量，通过该低维连续稠密的向量（每个元素不为0）的每个元素来表达整个网络。

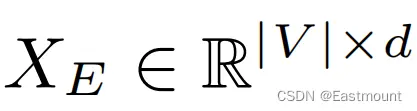
利用这些结构特征，我们将反映连接信息的Embedding和反映节点本身的特征连接，用来帮助分类决策。这些特征是通用的，可以用于任何分类算法（包括迭代方法）。然而，我们认为这些特性的最大优势是它们很容易与简单的机器学习算法集成。它们在现实世界的网络中能够被有效地扩展，我们将在第6节中展示。

4.网络连接的特征表示

该部分主要是描述Embedding。我们希望DeepWalk学到的Embedding（特征表示）具有下列特性：

• 适应性（Adaptabilty）：真实网络在持续地演化，新的节点和关系出现时不需要再重新训练整个网络，而是能够增量或在线训练。换句话说，网络的拓扑结构随着网络新的节点和连接动态变化。
• 社区意识（Community aware）：应该反映社群的聚类信息，如图1所示，属于同一个社区的节点有着相似的表示，网络中会出现一些特征相似的点构成的团状结构，这些节点表示成向量后也必须相似。这允许在具有同质性的网络中进行泛化。
• 低维（Low dimensional）：当标记数据稀缺时，低维模型可以更好地扩展并加速收敛和推理（防止过拟合）。即每个顶点的向量维度不能过高。
• 连续（Continuous）：低维向量应该是连续的，每个元素的细微变化都会对结果有影响，并且能拟合平滑的决策边界，从而实现鲁棒性更强的分类任务。

DeepWalk是通过一连串随机游走序列来对节点进行嵌入（或表示）的，并是有最初的语义模型（Word2Vec）进行优化。接下来，我们将简单回顾随机游走和语言模型的知识。

(1) Random Walks

假设将一个起始点v(i)的随机游走表示为W(vi)，对应的随机过程（stochastic process）定义为：

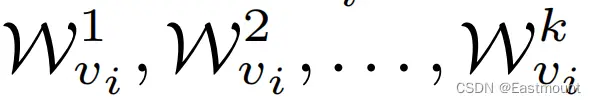
其中，k表示随机游走的第k步，v(i)表示起始点，之后的第k+1节点是从第k个节点的邻居节点中随机选择一个，属于均匀的随机游走。

随机游走已被应用于内容推荐和社区检测领域中的各种相似性度量问题。通过该方法将离得近且容易走动（或连通）的节点聚集。随机游走也是输出敏感类算法的基础，这些算法利用随机游走来计算与输入图大小相关的局部社区结构信息。

• Random Walk：假设相邻节点具有相似性
• Word2Vec：假设相邻单词具有相似性

这种局部结构信息可以促使我们利用一连串的随机游走来提取网络的信息。除了捕获社群信息外，随机游走还有其它两个比较好的优点。

• 并行采样
• 在线增量学习（迭代学习不需要全局重新计算）

(2) Connection: Power laws（幂律分布）

选择在线随机游走算法作为捕获图结构的雏形后，我们现在需要一种合适的方法来捕获这些信息。如果连通图的度（degree）分布遵循幂律分布（即无标度图，重要节点），我们观察到顶点在随机游走中出现的频率也将遵循幂律分布。

• 随机网络：节点的度服从正态分布
• 真实世界网络：属于无标度网络，比如社交网络存在大V、银行客户存在富翁等，存在大型中枢节点，此时服从幂律分布（长尾分布或二八分布）

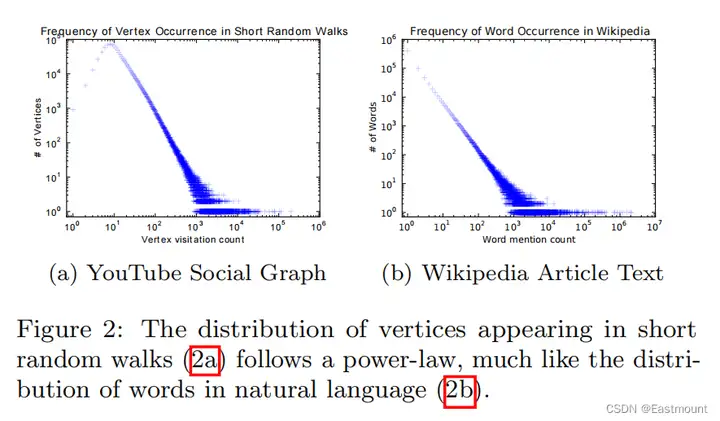
图2中展示了幂律分布现象，图2(a)是一个无标度图一系列随机游走的分布图，图2(b)是英文维基百科上的10万篇文章的单词幂律分布图。

• 图2(a)的横轴表示被媒体提及次数，纵轴表示节点个数（UP主数量）
• 图2(b)的横轴表示某个单词被采样到的次数，纵轴表示单词数，比如the\an\we出现较多

幂律分布参考我的前文：

• [python数据分析] 简述幂率定律及绘制Power-law函数 - Eastmount

为什么介绍这部分内容呢？

我们工作的一个核心贡献是将用于自然语言模型（幂律分布或Zipf定律）的技术可以用在图结构中建模（图数据挖掘）。换句话说，真实世界中，只有极少部分的单词被经常使用，或极少部分的节点被经常使用。

(3) Language Modeling

语言模型的目标是估计一个特定的单词序列出现在一个语料中的似然概率（likelihood）。换句话说，给定一系列单词W，通过上文的前n-1个词来预测第n个词。最近的表示学习研究就聚焦于利用神经网络语言模型来实现词的表示。

• 语言模型能反映一句话是否自然、高频或真实存在。

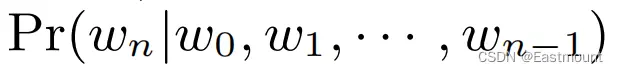
在本文中，我们提出了一种语言模型的推广，通过一系列的随机游走路径来进行建模。 随机游走可以被看作是一种特殊语言的短句或短语，节点类比成单词，通过前i-1个节点来预测第i个节点（预测访问顶点vi的可能性）。公式如下如下：

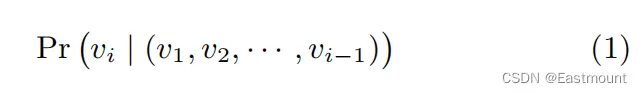
然而，本文希望利用的是节点的Embedding，而不是节点本身，如何解决呢？
我们的目标是学习一个隐式表示，因此引入一个映射函数Φ，即取出对应节点的Embedding。

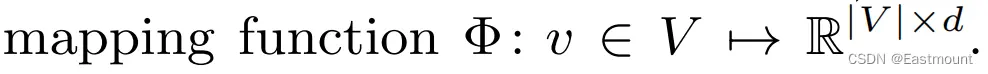
接着我们就可以用公式(2)完成计算，通过前i-1个节点的Embedding来预测第i个节点。该问题是要估计它的似然概率 。

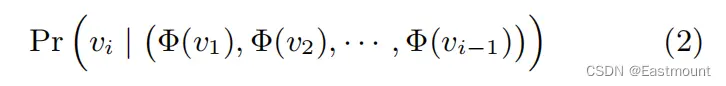
然而，随着随机游走长度的增加，计算这个条件概率就变得不可行了（n个概率连续相乘结果太小）。

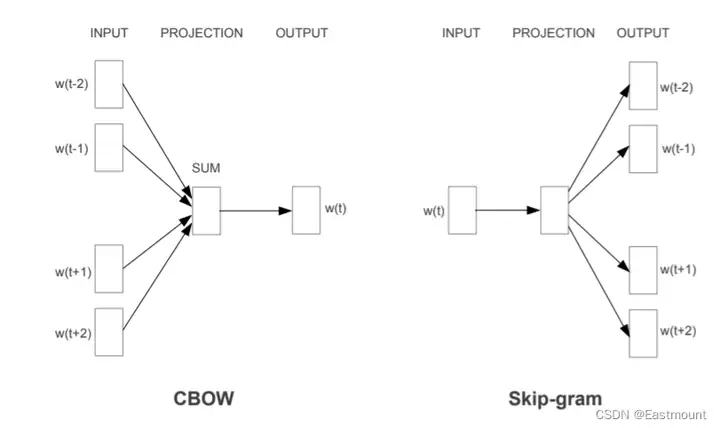
最近语言模型[27,28]（Word2Vec）很好地解决了这个问题。它可以利用周围上下文来预测中间缺失的单词（CBOW），也可以利用中心词去预测上下文单词（Skip-gram），从而构建自监督场景。

• [27] T. Mikolov, K. Chen, G. Corrado, and J. Dean. Efficient estimation of word representations in vector space. CoRR, abs/1301.3781, 2013.

Word2Vec将单词编码成向量如下图所示：

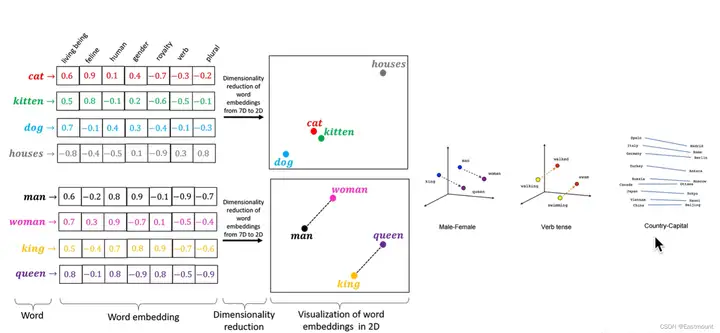
其次，上下文是由同时出现在给定单词的左右两侧的单词组成的。最后，它消除了问题的顺序约束，而是要求模型在不知道单词与给定单词之间的情况下，最大化上下文中任何单词出现的偏移的概率。

DeepWalk(Skip-gram)的损失函数定义如下（优化问题），最大化似然概率：

• 我们期待通过大量的随机游走序列训练，迭代地去优化Φ中的每一个元素，直到这个函数收敛或损失函数最小化，此时的Φ就是每个节点的Embedding。

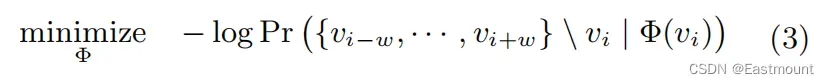
该方法对于图嵌入（表示学习）非常适用。

• 随机游走生成的顺序没有意义，符合当前场景，能很好地捕获邻近信息。
• 模型较小能加快训练时间。

方程3的优化问题：

• 具有相同邻居节点将获得相似的表示（编码共引相似）

总而言之，本文提出一种图嵌入的表示方法，通过结合随机游走和语言模型，能将图的每个节点编码为一个连续、稠密、低维的向量（Embedding），其包含了社群的语义特征，适用于各种变化的网络拓扑结构。==

5.本文方法

该部分将详细介绍该算法的主要组件及变体。同各种语言模型算法一样，需要构建语料库和词汇表。在DeepWalk中，语料库就是一系列的随机游走序列，词汇表就是节点集合本身（V）。

(1) Algorithm: DeepWalk

该算法的详细描述如下图所示：

a) SkipGram

SkipGram是一种语言模型，旨在利用中心词去预测上下文单词，它能反映词和词的共现关系，即使句子中出现在窗口w中的单词共现概率最大化。它使用一个独立假设来近似方程3中的条件概率，SkipGram计算Pr的算法如下：

• 通过中心节点的Embedding和上下文的某个节点的Embedding做向量的数量积。

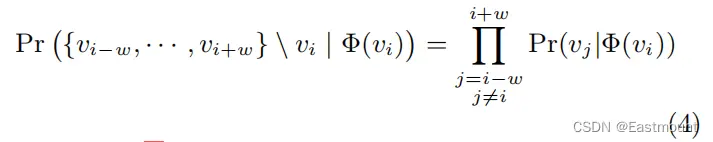
算法2是SkipGram的具体流程。给定vj表示，我们希望在随机游走中最大化它邻居的概率（算法第3行）。此外，它也会遇到和Word2Vec相同的问题。当节点较多时，会有数以万亿的分类预测，其分母会很大。因此，为加快训练时间，我们使用分层Softmax来近似概率分布。

 

b) Hierarchical Softmax

分层Softmax计算如下，它会将顶点分配给二叉树的叶子节点，将预测问题转化为层次结构中特定路径的概率最大化。

• 时间复杂度从O(n)降至O(log(n))

前一篇Word2Vec论文中已详细介绍：

• Hierarchical Softmax：Huffman树将较短的二进制代码分配给频繁出现的单词，减少需要评估的输出单元的数量。

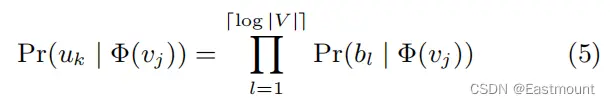
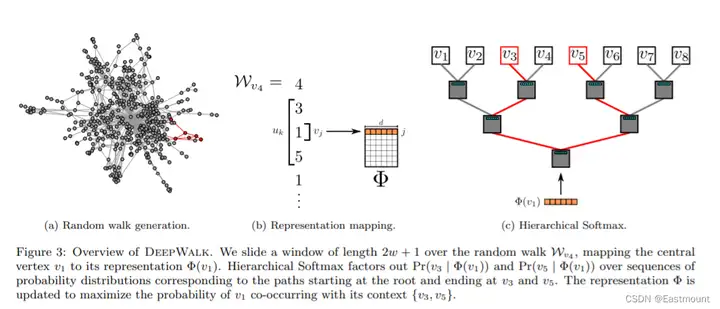
如图3c所示，原来的八分类问题转换成了3个二分类（log2(8)=3）。图中，最上层为叶子节点（8个），第二层和第三次的灰色方块为非叶子节点，即逻辑回归二分类器（7个），其参数量和Embedding维度一致。V3和V5是标签，两条红色先为对应的路径，会按照公式计算对应的损失函数并更新Embedding。

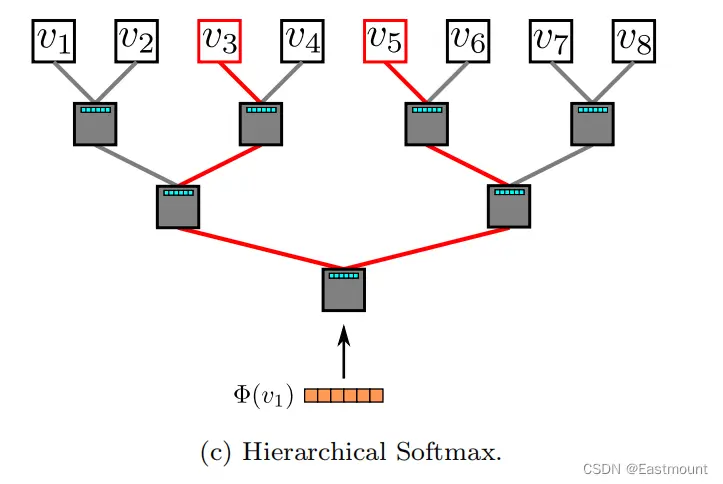
接着详细分析图3。

• 首先，图3(a)表示从图中随机游走采样出一个节点序列（红色标注）；
• 然后生成图3(b)所示的映射关系，v4表示4号节点，输入中心节点（v1）来预测上文和下文的节点，每侧窗口宽度w=1，通过查表得到中心节点v1映射对应的表示Φ(v1)；
• 最后，将该中心词的向量输入到分层Softmax中（图3c），由于v3和v5都是标签，两条路径回各自计算损失函数，再各自优化更新，这里存在两套权重，分别是：N个节点的D维向量，N-1个逻辑回归（每个有D个权重），这两套权重会被同时优化。

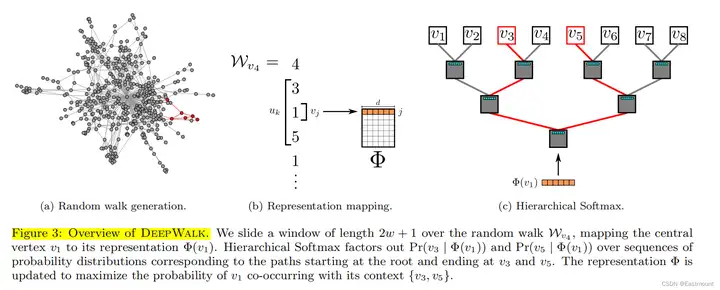
Pr(bl | Φ(vj)) 可以通过一个二分类器来建模，该分类器被分配给节点bl的父节点，如式6所示：

• 公式的指数表示词的Embedding和逻辑回归的权重的乘积，再通过Sigmod函数输出一个后验概率。

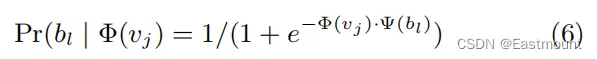
总之，我们通过在随机游走中分配更短的路径来加快训练过程（Hierarchical Softmax），霍夫曼编码可以减少树中频繁元素的访问时间。

c) Optimization（优化）

(2) Parallelizability

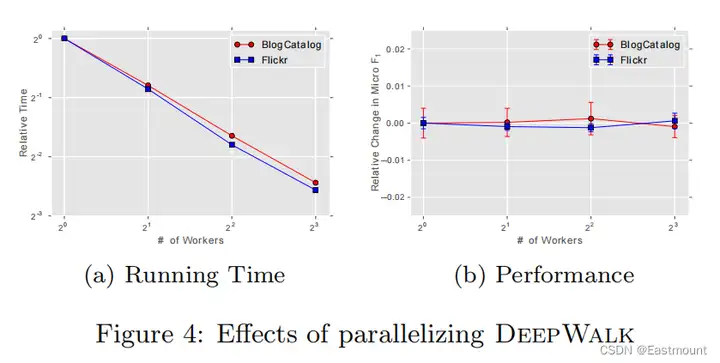
可以通过多线程异步并行（集群）来实现DeepWalk，ASGD梯度通过MapReduce实现。实验结果如图4所示，证明了加速的有效性（性能不变&加速）。

(3) Algorithm Variants

变种算法主要包括：

• Streaming
  在未知全图时，直接通过采样出的随机游走训练Embedding，新的节点会增量对应的Embedding
• Non-random walks
  不随机的自然游走

6.对比实验

(1) 数据集和Baseline方法

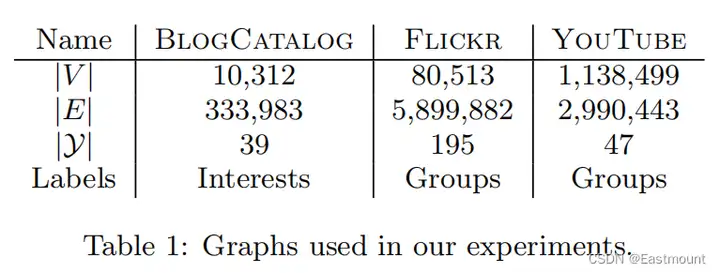
实验包括三个数据集。

• BlogCatalog：博客作者提供的社会关系网络，标签代表作者提供的主题类别。
• Flickr：照片分享网站，作者之间的联系网络，标签代表用户的兴趣组。
• YouTube：视频分享网站，用户之间的社交网络，标签代表喜欢视频类型（如动漫和摔跤）的观众群体。

对比方法如下：

• SpectralClustering（谱聚类）
• Modularity（模块化）
• EdgeCluster
• wvRN
• Majority

(2) 实验结果

评估指标包括：

• T_R：标注的节点比例
• Macro-F1
• Micro-F1

实验参数：

• γ =80：每个节点被采样的次数
• w = 10：滑动窗口
• d = 128：向量的维度
• t = 40：游走的节点长度

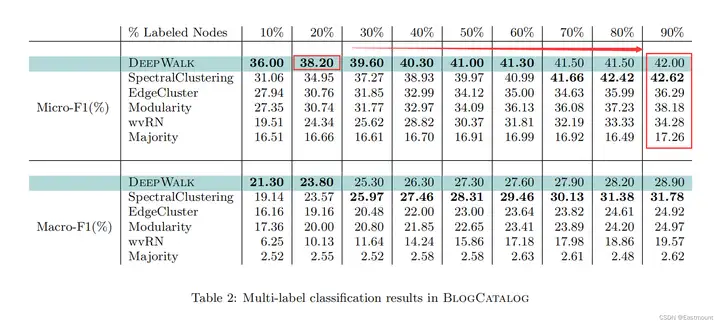
通过one-vs-rest逻辑回归分类器解决多分类问题（构建多个二分类实现多分类预测）。整个实验结果如下所示：

• DeepWalk预测效果优于其它算法
• 当标注节点比例越小，DeepWalk效果表现越好，甚至只用20%的数据比其他算法用90%的数据更强

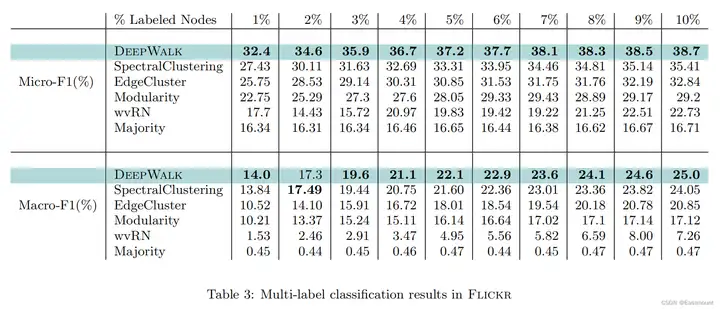
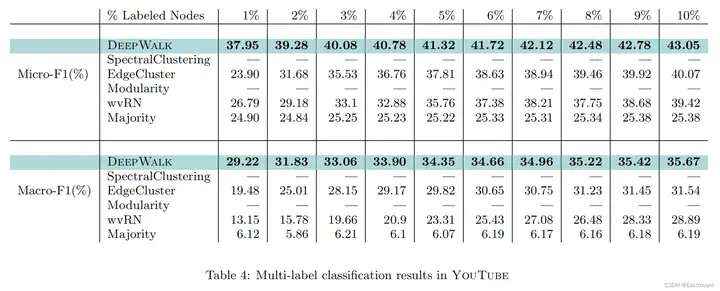
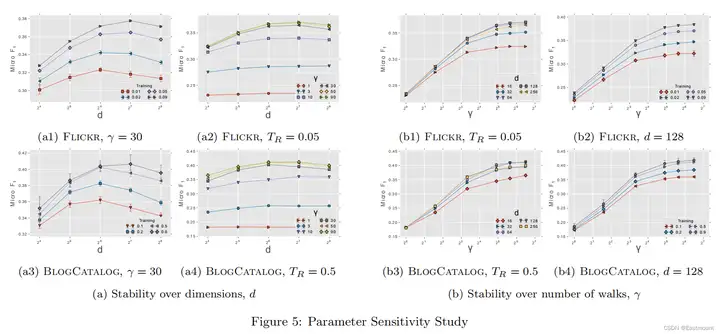
参数敏感性对比实验如下图所示：

• TR会影响最优d，TR越大效果越好
• γ越大，效果越好，但边际效果逐渐降低

7.个人感受

首先，本文在相关工作中进一步突出DeepWalk的优势，具体如下：

• DeepWalk是通过机器学习得到的隐式表示（Embedding），而非人工统计构造。
• DeepWalk不考虑节点的标注和特征信息，只考虑Graph的连接信息，属于无监督学习。后续可以利用无监督的Embedding和标注信息训练有监督的分类模型。
• DeepWalk是一种只使用Graph的局部信息且可扩展的在线学习方法，先前的方法都需要全局信息且是离线的。
• 本文将无监督表示学习思路应用于图中。

综上所述，本文提出了DeepWalk，一种用来学习隐式网络表征的新颖方法。通过随机游走序列捕捉网络的局部信息，再将每个节点编码成向量Embedding，能有效表征原图的结构规律。通过实验证明了DeepWalk多分类的有效性。

下图是子豪老师的总结：

个人感受：

DeepWalk是图嵌入（Graph Embedding）的开山之作，图神经网络领域非常重要的一篇论文。其核心思想是将Word2vec应用在图中，语言模型和图网络的转换非常精妙，DeepWalk将图当作语言，节点当作单词来生成Embedding。在DeepWalk中，它通过随机游走算法从一个节点随机到另一个节点，从而将网络化数据转换成一个序列（Sequence），再无监督地生成对应的Embedding，其扩展性、性能和并行性都表现良好，且支持在线学习。此外，上一篇文章我们介绍了Word2Vec，推荐大家结合阅读。

最后，好文章就是好文章，真心值得我们学习。同时，本文除了作者阅读原文外，也学习了B站同济子豪老师的视频，强烈推荐大家去学习和关注。在此表示感谢，他也说到，本文可能存在一些语法错误，但最重要的是Idea，大家写论文也优先把握好的Idea和贡献，花更多精力在那方面。

 

点击关注，第一时间了解华为云新鲜技术~

标签：DeepWalk,随机,Embedding,游走,表征,节点,向量
From： https://www.cnblogs.com/huaweiyun/p/17043255.html