(昨天发病写题解,结果一看早就截止了)
前置知识:数列分块
我们先看一个式子
\[\sum_{k=1}^{n} \lfloor \sqrt k \rfloor \]化简
我们稍微枚举一下,就会发现这样一个性质
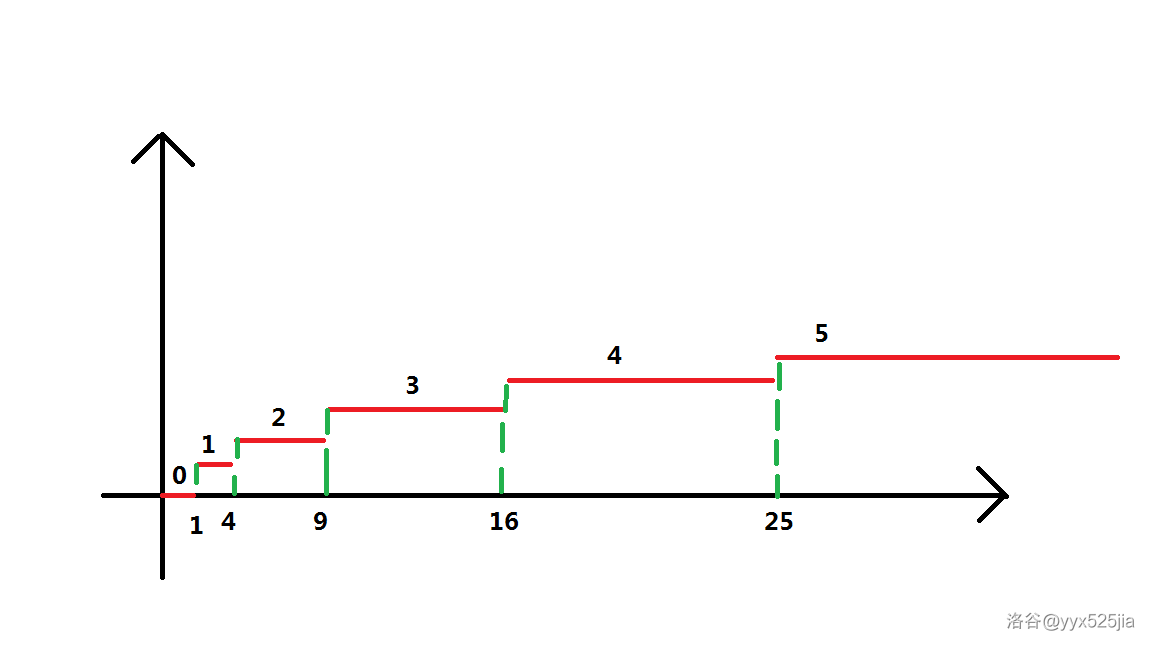
这个数列是一段一段的,而且第i段的长度是 \(i^2-(i-1)^2\),第i段的值是 $ i-1 $,那么我们可以直接化简成线段长度* 线段值
此时我们不禁思考:

数学家们和百度告诉我们:

所以我们可以设一个
\[\sum_{k=1}^{n}f(i) \lfloor \frac{n}{i} \rfloor \]\(f(i)\)可以是任意一个函数
那么此时我们自然贪心的想要一个对于这一类式子的统一的优化,我们可以仿造之前对例4的处理,仍然把它分成整块区间的区间长度*区间值(其实也就是 \(f(i)\) ) ,至于被从中间截断的,我们直接特判就完事,我们现在需要的是:

我们关注到一个性质: $ 一段区间的函数值是相同的。$
所以我们就可以列出一个等式
稍加化简,可以得到
\[r = \lfloor \frac{n}{\lfloor \frac{n}{l} \rfloor} \rfloor \]就这样,我们得到了l和r之间的关系式,因此,一个普遍的优化就这样推出来了
回归正轨:P2261 [CQOI2007]余数求和
题意:
给出正整数 n 和 k,请计算
注:mod就是%
给出n,k
$ 对于 100% 的数据,保证 1 \leq n, k \leq 10^9 $
首先,我们应该知道%的本质
\[a\bmod b=a-b* \lfloor \frac{a}{b} \rfloor \]所以我们直接返璞归真
\[G(n, k) = \sum_{i = 1}^n (k-i* \lfloor \frac{k}{i} \rfloor) \]使用把k抽出来
\[G(n, k) = \sum_{i = 1}^n k-\sum_{i = 1}^n (i* \lfloor \frac{k}{i} \rfloor) \]把k化简
\[G(n, k) = n*k-\sum_{i = 1}^n (i* \lfloor \frac{k}{i} \rfloor) \]我们发现,这不就是个数列分块嘛,所以我们自然而然的使用优化。
总共有k种取值,所以时间复杂度就是\(O(\sqrt k)\)的。
然后就直接模拟按照刚刚的推论做就完事
注意开long long
#include<bits/stdc++.h>
#define for1(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
#define mp(a,b) make_pair(a,b)
using namespace std;
ll n,k;
int main()
{
cin>>n>>k;
ll ans=n*k;
ll l=1,r=0;
while(l<=n)
{
l=r+1;
if(k/l!=0)
r=min(k/(k/l),n);
else //当k/l等于0时意味着已经触碰到了边界n
r=n;
ans-=(k/l)*(r-l+1)*(l+r)/2;
}
cout<<ans<<endl;
return 0;
}