线性 DP

概述

• 线性 DP 并没有明确的定义。

• 我个人认为，广义的线性 DP 指的是满足以下几个条件的 DP：

  • 存在至少一维可以线性推进;

    • 区间 DP 可以满足这个要求，只要在状态里放 \(len\)。在这一意义下，区间 DP 是“线性推进的一维为区间长度”的特化线性 DP。

    • 状压 DP 显然不满足，即使状态为 \(dp_{sta,i}\)，占据主导地位的“层”实质上是 \(sta\) 的 \(ppc\)，当然你如果非说在这一不存在的“维”上线性那...我也只能同意...

    • 数位 DP 显然满足。在这一意义下，数位 DP 是“线性推进的一维为考虑到哪个数位”的特化线性 DP。

    • 树形 DP...过于特殊了吧？高度依赖树形结构。甚至也许我们应该认为线性 DP（链上的）是特化的树形 DP（树上的）...

  • 转移较为简单，具有某种意义上的线性，通常可以使用网格图刻画；

    • 这个主要是把一些高度依赖记忆化搜索/拓扑排序的 DP 划出去。

    • 这种转移的简单往往是从状态设计的精巧而来的。具体来讲的话，DP 的本质在很大程度上就是抓取状态的关键信息...

    • 我们以背包 DP 为例吧。

      • 如果把选的集合视为点，物品视为边，直接建图，点数显然趋于指数级；

      • 而背包 DP 离谱的状态设计则把这样一个点数超多，边（也就是点的关系，也即转移）超复杂的图压成了一个简单网格图，然后偏移连边，某种意义上这里的层界就是物品。

  • 通常较为容易进行各种优化。

    • 至少我见到的大部分 DP 优化都是在线性 DP 上做的。

• 我们会把线性 DP 作为 DP 的概述来使用。换言之，我们会在里面谈到很多 DP 的共性特点。

• 实际实践中，线性 DP 的形式也是极不同的。故此处不给出更多的状态/初始化/转移上的共性，我们直接起各种类吧。

子序列式问题

• 典型代表如 LCS 和 LIS。其实两者的 DP 形式共性不大...

• 特点是对某种意义下的子序列求最长。好吧我们还是来看各个子类...

最长上升子序列（Longest Increasing Subsequence,LIS）问题

• 经典模型为求一个串的最长上升子序列。不降/下降等问题显然与此问题本质同构。

• 深入剖析的话，这实质上是二维偏序问题，即 \(i<j,a_i<a_j\)。也因此，它具有极重要的地位。

• 通常复杂度（好像也是理论下界）是 \(O(n\log n)\)。下面给出几种能达到这个复杂度的 DP 设计：

• 结尾导向法：

  • 状态设计：\(dp_{i,len}\) 表示考虑了前 \(i\) 个数字，长度为 \(len\) 的上升子序列结尾最小是多少。

    • 实际上第一维常常省略掉，因为 \(dp_i\) 和 \(dp_{i+1}\) 几乎相同，不省略不仅空间炸而且时间炸。下面使用省略前的状态，但实际实现中请省略。

  • 初始化：\(dp_{x,0}=-\infty,top=0\)。

    • \(top\) 是一个辅助转移用的指针，表示当前最长上升子序列长度。

  • 状态转移：一般我使用递推转移。记 \(k\) 为 \(a_i\) 在 \(dp_{i-1}\) 上的 \(lower\_bound\)（但不许相等），则有 \(dp_{i,j}=\begin{cases} dp_{i-1,j} & j\neq k+1 \\ \min(dp_{i-1,j},a_i) & j=k+1\end{cases}\)。

    • 特别地，如果 \(k=top\)，那么 \(top=top+1\)。

  • 复杂度 \(O(n\log n)\)，也可以使用线段树上二分或 set 来实现，但可能常数更大。

• 长度导向法：

  • 状态设计：\(dp_{i,j}\) 表示考虑完前 \(i\) 个数字，结尾为 \(j\) 的 LIS 长度最大是多长。

    • 同样地，建议省略第一维。

  • 初始化：\(dp_{0,0}=0\)。

  • 状态转移方程：\(dp_{i,j}\begin{cases} dp_{i-1,j} & j\neq a_i \\ \max(dp_{i-1,j},\max_{k<j}(dp_{i-1,k})+1) & j=a_i\end{cases}\)。非常恶心。

  • 这个的优点主要在于其具有一定的在线性。显然这个东西是用线段树来维护的，而它的本质是枚举 \(i\)（第一维），求 \(a_i\)（第二维）的前缀 \(\max\) 然后插入到 \(a_i\) 上，具有明显的在线风格。

  • 更进一步地，结尾导向法也可以用线段树来做在线，不过是把 \(a_i\) 当做第一维来枚举罢了。

  • 这两个 DP 状态同构。相关定义请看 LCS 那边。

  • 哦，复杂度 \(O(n\log n)\)。

• 钦定结尾法：

  • 状态设计：\(dp_i\) 表示以 \(a_i\) 结尾的最长上升子序列长度。

    • 这一状态设计是较为经典的极小状态集思想的体现。

    • 所谓“极小状态集”，指的是 DP 状态应当使用极小的状态来表示信息，如果某两维能够互相推出，就应当舍去一个。

    • 在这里的体现就是 \(dp_i\) 的状态虽然记录的是“用了 \(1\sim i\) 这一段”，但既然是以 \(a_i\) 结尾，那么我们也就知道了对应 LIS 的结尾，不需要为了转移额外记录 LIS 的结尾。

    • 这一思想在 \(\text{P2051 [AHOI2009] 中国象棋}\) 也有较为经典的体现：不需要记录多少列没有炮，因为若记 \(l\) 为没有炮的列数，则总有 \(j+k+l=m\)，容易由 \(j,k\) 推出没有炮的列数。

  • 初始化：\(a_0=-\infty,dp_0=0\)。

  • 状态转移方程：\(dp_i=\max_{j=1}^{i-1}(dp_j+1)(a_j<a_i)\)。

  • 复杂度 \(O(n\log n)\)，但是这个可以树状数组。而且输出方案也比较舒服一些（不过这需要把 ta 魔改一下）。

最长公共子序列（Longest Common Subsequence，LCS）问题

• 经典模型为求两个字符串的最长公共子序列。

• 各做法复杂度不一而同但都有应用场景，下面给出几种常用的 DP 设计：

• 结尾导向法：

  • 状态设计：\(dp_{i,len}\) 表示 \(S_1\) 考虑了前 \(i\) 位，长为 \(j\) 的 LCS 在 \(S_2\) 的结尾最前是多少。

  • 初始化：\(dp_{0,0}=0\)。

  • 状态转移方程：\(dp_{i,len}=\min(dp_{i-1,len},S_2.find(S_{1,i},dp_{i-1,len-1}))\)。

    • 这里的 \(find\) 利用离散字符集后对每个字符记录出现位置，然后二分查找，做到 \(O(\log |S_2|)\)。

  • 复杂度 \(O(|S_1|^2\log |S_2|)\)，\(|S_1|,|S_2|\) 不同阶时表现较好。

• 长度导向法：

  • 状态设计：\(dp_{i,j}\) 表示 \(S_1\) 考虑了前 \(i\) 位，\(S_2\) 考虑了前 \(j\) 位，LCS 最长多长。

  • 初始化：\(dp_{0,0}=0\)。

  • 状态转移方程：

    • 泛用：\(dp_{i,j}=\max(dp_{i,j-1},dp_{i-1,j})\)。

    • 当 \(S_{1,i}=S_{2,j}\)：还有 \(dp_{i,j}=\max(dp_{i-1,j-1}+1)\)。

  • 这一 DP 的状态-转移网格图很有趣：

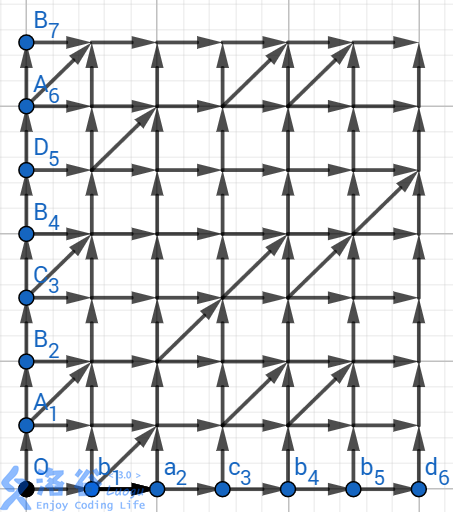
  • 实质上可以认为是斜边边权 \(1\)，纵横边边权 \(0\)，跑最长路。

  • 复杂度 \(O(|S_1||S_2|)\)，\(|S_1|,|S_2|\) 同阶时表现较好。

• 这两个 DP 有着同构状态。所谓同构状态，狭义来讲，指的就是各维（等号右边的也算一维）本质相同，只是位置不同（主要在于把哪一个放到等号右边）的 DP 状态。

• 广义的同构状态是通过设计合适的初始化和转移能够等价地描述同一过程的多个状态。

• 状态同构的 DP，转移和复杂度可能是不同的（LCS 就是一个很好的例子）。通常，选取哪个作为实际的 DP 状态，主要考虑以下几方面：

  • 状态数。把太大的放到等号右边。

    • 这在背包 DP 里特别典型：取 \(\sum w,\sum c\) 中较小的一个扔到等号左边。

    • \(\text{P6879 [JOI 2020 Final] スタンプラリー 3}\) 也是一个很好的例子，把答案放到维度里了。

  • 转移复杂度。选取转移复杂度较小的 DP 设计。

    • 譬如 LCS，因为实际题目中一般有 \(|S_1|,|S_2|\) 同阶，通常使用第二个 DP。

• 转为 LIS 法：

  • 此做法想要优秀复杂度的话，高度依赖序列不可重这一性质。

  • 我们来分析一些性质。之前说了，LIS 的本质是二维偏序，那 LCS 呢？

  • 也是二维偏序，没想到吧！考虑不可重的简单情况，分别记 \(k_{1,i},k_{2,i}\) 为 \(i\) 在 \(S_1,S_2\) 中的出现位置，实质上是求一个序列使得 \(k_{1,i}<k_{1,j},k_{2,i}<k_{2,j}\)。

  • 那自然是先把所有元素按 \(k_1\) 排序，也即以 \(S_1\) 为基础来做 DP。求出所有 \(k_2\)，问题变成在 \(S_1\) 的 \(k_2\) 数组上求 LIS，容易 \(O(n\log n)\) 解决。

  • 这个做法也可以推广到可重序列：

    • 以 bacac 和 abacc 为例，将 \(k_{2,i}\) 展开为一个单调递降的 vector，即，\((2),(3,1),(5,4),(3,1),(5,4)\)。

    • 然后对该序列求 LIS。倒序理由显然，防止同一个字符被重复选取，有点类似多重背包。

    • 随机数据下表现较好，但显然可以被全同的序列卡到 \(O(|S_1||S_2|\log |S_1|)\) 的复杂度。

• bitset 优化法：

  • 做差分然后上奇怪的 bitset 优化，我不会，参看位运算求最长公共子序列（显然不是我的）。

  • 时间 \(O(\dfrac{|S_1||S_2|}{w})\)，空间不劣于 \(O(\dfrac{|S_1|^2}{w})\)（对字符离散化）。

  • LOJ #6564. 最长公共子序列。

最长公共上升子序列（Longest Common Increasing Subsequence，LCIS）问题

• 经典模型为求两个串的最长公共上升子序列。

• 基于两串长度是否同阶，主要有两种 DP：

• 结尾导向法：

  • 状态设计：\(dp_{i,len}\) 表示以 \(S_{1,i}\) 结尾，长度为 \(len\) 的 LCIS 在 \(S_2\) 的结尾最前是多少。

  • 初始化：\(S_{1,0}=-\infty,dp_{0,0}=0\)。

  • 状态转移方程：\(\begin{aligned}dp_{i,len} & =\min_{j<i\And S_{1,j}<S_{1,i}}(S_2.find(S_{1,i},dp_{j,len-1}+1))\\ & =S_2.find(S_{1,i},\min_{j<i\And S_{1,j}<S_{1,i}}dp_{j,len-1}+1)\end{aligned}\)。

    • \(\min\) 部分可以用树状数组来做，转移本身有 \(j<i\) 的固有顺序，插到 \(S_{1,i}\) 处就好。

    • \(find\) 部分可以对字符集离散然后记录出现位置上去二分查找。这部分可能有 \(O(|S_2|\log |S_2|)\) 的预处理复杂度，请注意。

  • 复杂度 \(O(|S_1|^2\log |S_2|)\)，\(|S_1|,|S_2|\) 不同阶时表现较好。

• 长度导向法：

  • 状态设计：\(dp_{i,j}\) 表示使用/浪费了 \(S_1\) 的前 \(i\) 个，以 \(S_{2,j}\) 结尾的 LCIS 长度最大是多少。

    • 我们看到这个设计的核心思路是 LCS 风格的状态，然后 LIS 风格的转移。

  • 初始化：\(dp_{0,0}=0\)。

  • 状态转移方程：\(dp_{i,j}=\begin{cases} dp_{i-1,j} & S_{1,i}\neq S_{2,j}\\ \max_{k<j \And S_{2,k}<S_{1,i}}(dp_{i-1,k})+1 & S_{1,i}=S_{2,j} \end{cases}\)。

    • 可以看出，正如某些 LIS 做法一样，这个 DP 的第一维可以压掉。

    • 之所以 \(a_i=b_j\) 时不考虑继承是因为用一个 \(l<i\) 和用 \(i\) 作为 \(a\) 中的结尾并没有什么区别，毕竟 \(a\) 这边是基础，是层。

  • 显然可以使用前缀最大值优化做 \(O(|S_1||S_2|)\)，\(|S_1|,|S_2|\) 同阶时表现较好。

    • \(S_{1,i}\) 的限制对于同一层的转移是固定的，每次考虑新增的 \(j\) 作为 \(k\) 就好。

• 实际上这两者都钦定了结尾。生活所迫啊！

  • 一定要钦定以 \(S_{1,i}\) 和 \(S_{2,j}\) 结尾的话，转移会非常僵硬（难以邻项转移了），至少我只会 \(O(|S_1||S_2|\log |S_1|\log |S_2|)\) 的树套树二维前缀最大值做法，而且转移顺序非常恶心，是以值升序为第一关键字，以下标升序为第二关键字的顺序。

背包式问题

• 典型代表如 01 背包，完全背包和多重背包这三个经典背包问题。

• 较常见的推广的有分组背包，依赖背包，多维背包，泛化物品背包等。

• 常见的问题主要有可达性，\(K\) 优解，\(K\) 优解方案数，字典序最小的 \(K\) 优解等。

• 常用优化有二进制拆分，单调队列，分层 bfs ，基于四边形不等式的分治优化等。

• 不可小觑啊！说回来，谈谈它们的共性。

• 特点如下：

  • 给出一些物品，物品的本质是一个二元组（这里不考虑多维背包）\((c,w)\)。

  • 求 \(\sum c\leqslant lim\) 的条件下：

    • 能否恰有 \(\sum w=req\)。

    • 求第 \(k\) 大的 \(\sum w\)。

    • 其他问题。

    • 及满足对应要求的决策方案，可能还及字典序最小的方案。

  • 视题目不同，物品有不同的选取限制，可能是数量上的/顺序上的/...，泛化物品背包甚至将物品重构。

• 状态设计通常为 \(dp_{i,j}\) 表示考虑完前 \(i\) 个/种/组物品，共花 \(j\) 的代价的最大总价值。有时我们也会采用其同构状态。

• 初始化通常为 \(dp_{0,0}=0\)。

• 状态转移方程...最朴素的是 \(dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-c_i}+w_i)\)，但实际上视情况而定，不一而同。

• 经典三问的复杂度都可以做 \(O(n\min(\sum c,\sum w))\)，其他的具体问题具体分析。

• 注意，这是伪多项式时间。另外分层 bfs 在 \(\sum c\) 和 \(\sum w\) 都过大时也许能够做比经典复杂度优秀得多的复杂度。下面默认 \(\sum c\leqslant \sum w\)。

• 把两个背包合并到一起的复杂度是铁铁的 \(O((\sum c)^2)\)；在大部分背包问题中，这是一个很绝望的复杂度。如果有机会就多考虑暴力转，合并这个思路往往是没有前途的，因为暴力转可以设法重复利用转过的部分，而合并断无机会。

01 背包

• 经典模型如下：

  • 有 \(n\) 个物品，每个物品有代价 \(c\) 和价值 \(w\)。

  • 每个物品都只能选一遍。

  • 求选取的物品的 \(\sum c\leqslant lim\) 的前提下的最大 \(\sum w\)。

• DP 设计如下：

  • 状态设计：\(dp_{i,j}\) 表示考虑完前 \(i\) 个物品，共花 \(j\) 的代价，所得的最大总价值。有时我们也会采用其同构状态。

  • 初始化：\(dp_{0,0}=0\)。

  • 状态转移方程：\(dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-c_i}+w_i)\)。后项需要 \(j\geqslant c_i\)。

  • 通常会压掉 \(i\) 这一维，然后倒序转移以防止把同一个物品选了多遍。

• 复杂度 \(O(n\sum c)\)。

完全背包

• 经典模型如下：

  • 有 \(n\) 种物品，每种物品有代价 \(c\) 和价值 \(w\)。

  • 每种物品都有无限个，即可以选无数遍。

  • 求选取的物品的 \(\sum c\leqslant lim\) 的前提下的最大 \(\sum w\)。

• DP 设计如下：

  • 状态设计：\(dp_{i,j}\) 表示考虑完前 \(i\) 个物品，共花 \(j\) 的代价，所得的最大总价值。有时我们也会采用其同构状态。

  • 初始化：\(dp_{0,0}=0\)。

  • 状态转移方程：

    • 通常我们使用一种基于压维的转移。下面的内容认为把 \(i\) 这一维压掉了。

    • \(dp_j=\max(dp_j,dp_j-c_i+w_i)\)。后项需要 \(j\geqslant c_i\)。

    • 该转移顺序进行，某种程度上是在“利用后效性”来实现把同一种物品选多次的效果。

• 复杂度 \(O(n\sum c)\)。

多重背包

• 经典模型如下：

  • 有 \(n\) 组物品，每组物品有代价 \(c\) 和价值 \(w\)。

  • 每组物品有 \(num_i\) 个。

  • 求选取的物品的 \(\sum c\leqslant lim\) 的前提下的最大 \(\sum w\)。

• 多重背包的求解主要有三种方式。我们下面依次谈一谈：

• 朴素 DP/01 背包拆分 DP（这里给出后者的实现，前者的实现缺乏启发性，且本质同构）：

  • 状态设计：\(dp_{i,j}\) 表示考虑完前 \(i\) 个物品（把同种物品拆成 \(num_i\) 个），共花 \(j\) 的代价，所得的最大总价值。有时我们也会采用其同构状态。

  • 初始化：\(dp_{0,0}=0\)。

  • 状态转移方程：\(dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-c_i}+w_i)\)。后项需要 \(j\geqslant c_i\)。

  • 复杂度 \(O(n\sum c\sum num)\)。

• 这一拆分太过粗糙。仔细考虑，我们希望的是“选取 \(0\sim num_i\) 个”的决策都能被选取，那么能否使用更高效的拆分方式，使得更少的 01 背包物品代表着那些决策？

• 正是任何一种合理进制！但 \(k\) 进制的任何一位都要有 \(k-1\) 件 01 背包物品，故显然二进制拆分最优。

• 二进制拆分优化 DP：

  • DP 本身同上，只是拆分物品时做二进制拆分。

  • 复杂度 \(O(n\sum c\sum \log_2 num)=O(n\sum c\log_2 \prod num)\)。

• 单调队列优化 DP：过于复杂，参看 单调队列优化 中的“单调队列优化多重背包”。

• 广义多重背包（同组物品只有 \(c\) 或 \(v\) 相同）：参见 DP 优化-分治优化一节。

• 三大经典模型看完了。那么，准备好迎接更多奇怪的限制、奇怪的物品和奇怪的优化了吗？

分组背包

• 分组背包的主要特点如下：

  • 存在 \(K\) 个限制，每个限制是一个集合 \(S\)。

  • 限制的形式是 \(S\) 内的物品只能选 \([L,R]\) 个/种/组（选 \(x\) 个种/组指的是在其中至少选了一个）。

• 主要的区分点在于这几个：

  • 集合是否可交，乃至于物品间的矛盾关系是否可以进一步泛化。

  • \(L\) 是否 \(=0\) 和 \(R\) 是否等于 \(|S|\)。

  • 物品是哪种背包意义下的物品。

• 这里我们先就最简单的情况进行讨论，即集合不可交，\(L=0,R=1\)。

• 为了方便，这里认为 \(S_1\cup S_2\cup \dots \cup S_K=n\)，不行就手动补一些 \(|S|=1\) 的集合。

• DP 设计如下：

  • 状态设计：\(dp_{i,j}\) 表示考虑完前 \(i\) 个集合的物品，共花 \(j\) 的代价，所得的最大总价值。可能改用同构状态。

  • 初始化：\(dp_{0,0}=0\)。

  • 状态转移方程：\(dp_{i,j}=\max(dp_{i-1,j},\max_{k\in S_i}(dp_{i-1,j-c_k}+w_k))\)。后项需要 \(j\geqslant c_k\)。

• 复杂度 \(O(n\sum c)\)。

• 更泛化的矛盾：

  • 集合可交：似乎只能状压。

  • 更严苛的限制，譬如 \(|S_i\cup S_j|\leqslant 1\)，或者不是集合而是区间，也许有更优的做法。

  • 进一步泛化矛盾的相关内容可以参看 状压 DP 中“依赖式问题”一节。

  • 特别地，考虑参看其中的 \(\text{P2051 [AHOI2009] 中国象棋}\)，其本质上是一个很像线性的状压，有极其简洁（几乎可以称为线性）的状态，且在对这道题目的分析中，我们讨论了 DP 的本质。

• 选 \([L,R]\) 个：

  • 考虑暴力。

    • 每个集合 \(O(\sum\limits_{k=L}^R C(|S|,k)\times k\times \sum c)\)。

    • 总复杂度 \(O(\sum\limits_{i=1}^K \sum\limits_{k=L_i}^{R_i} C(|S_i|,k)\times k\times \sum c)\)。

  • 考虑朴素。

    • 设计一个集合内的 DP。

      • 状态设计：\(dp_{i,j,sumc}\) 表示考虑了前 \(i\) 个，选了 \(j\) 个，总代价为 \(sumc\) 的最大总价值。

      • 初始化：\(dp_{0,0,0}=0\)。

      • 状态转移方程：\(dp_{i,j,sumc}=\max(dp_{i-1,j,sumc},dp_{i-1,j-1,sumc-c_i}+w_i)\)。啊显然这个 \(i\) 是可以压的。

    • 集合内 \(O(|S|R\sum c)\)，集合间合并 \(O((\sum c)^2)\)。

    • 总复杂度 \(O(\sum\limits_{i-1}^K|S_i|R_i\sum c+(K-1)(\sum c)^2)\)。

  • 不能 wqs 二分！

    • 乍一看似乎在 \(sumc\) 固定时 \(sumv\) 关于 \(k\) 单峰，然而并不是这样。

    • 考虑三种物品分别有 \(1,2,3\) 个，属性为 \((v_1,sumc),(v_2,\dfrac{sumc}{2}),(v_3,\dfrac{sumc}{3})\)。

    • 容易证明在 \(k=1,2,3\) 时决策方案唯一，于是只要适当构造 \(v\) 就 OK 了，很容易让它不凸。

      • 譬如 \(v_1=10,v_2=4,v_3=3\)，甚至不单调。

      • 主要思路就是 \(v_i>v_{i+1}\) 然后乱搞。

杂谈

P5888 传球游戏

• 题意略。

• 主要的有趣点在于把同质的人合起来，以及全局打 tag，翻转转移的 \(O(km)\) 妙妙思路。

P3147 [USACO16OPEN] 262144 P

• 题意略。

• 倍增思想的完美运用，巧妙地将区间问题转化成线性问题。

P2470 [SCOI2007] 压缩

• 参看区间 DP-复杂区间 DP。我把自己骗了，这是一道很妙的线性啊...

P1758 [NOI2009] 管道取珠

• 题意：

  • 给定两个 01 栈。每次可以从还有数字的任意栈顶取一个并加到序列尾。

  • 求 \(\sum\limits_{res} case_{res}^2\)，其中 \(res\) 是生成的序列，\(case\) 是生成方案数。

• 数据范围：\(n\leqslant 500\)。

• 首先来一个惊为天人的转化：题意所求等于两个游戏同时进行且结果相同的方案数。

• 理由就是双方各有 \(case\) 种方式达到。

• 然后考虑设计一个最简状态 DP：

  • 状态设计：\(dp_{i,j,k}\) 表示取了 \(i\) 次，第一个游戏的第一个栈取了 \(j\) 次，第二个游戏的第一个栈取了 \(k\) 次，两个游戏生成的序列相同的方案数。

  • 初始化：显然为 \(dp_{0,0,0}=1\)。

  • 状态转移方程：不想写...顺推来讲的话，就是如果栈里还有且相等，就转移过去，系数为 \(1\)。

• 妙啊！\(O(n^3)\)。

P8321 『JROI-4』沈阳大街 2

• 题意：给定排列 \(A,B\)，求 \(\frac{1}{n!}\sum\limits_P f(P)\)，这里 \(f(P)=\prod\limits_{i=1}^n \min(A_i,B_{P_i})\)。

• 超级妙妙题...做如下题意转化：

• 注意到这里 \(P\) 可以认为是一个 \(B\to A\) 的双射，显然顺序是没有关系的，且乘多少取决于较小值，故将 \(A,B\) 合并为一个单调不增的序列。

• 既然 \(P\) 是一个双射，那么这其实是一个匹配问题。我们依次考虑这个序列的每个元素，其有两种选择：

  • 做一个 \((A_x,B_y)\) 对中较大的一个，并留一个“插头”。

  • 做较小的一个，需要有一个对应的“插头”。

• 据此设计 dp 如下：

  • 状态设计：\(dp_{i,j}\) 表示考虑了该序列的前 \(i\) 位，构成了 \(j\) 个对的所有方案的权值总和。

  • 初始化：\(dp_{0,0}=1\)。

  • 状态转移方程：以 \(i+1\in A\) 为例，为

  \[\begin{aligned} & dp_{i,j}\to dp_{i+1,j} & k=1 \\ & dp_{i,j}\to dp_{i+1,j+1} & k=v_{i+1}[cnt_{B,i}>j] \end{aligned} \]
  • 其中 \(k\) 为转移系数。

• 得解，复杂度 \(O(n^2)\)。

• 就其本质而言，这还是拆 \(\min\) 然后分别算贡献的思想；其特殊处在于其需要一个垫材（较大值）和元素只能用一次，为了创造 dp 机会，混成序列。

• 规定在较大值处计算权值自然也是可以的，但可能导致挂的插头太多回收不了，这就是同构状态的东西了。