抄自这里,加了一些自己的理解吧,但本人数学水平属实不行。
不知道极值点偏移这个东西是从哪里发源起来的,可能是全国甲卷吧,感觉常规方法(指对称点作差)的重复性劳动没太大意义,变难无非是不等式同构套娃,反而我是感觉失去了出这种题型的本意,但你还是得做。
下文不妨设 \(x_1<x_2\)。
概述
大概解决这样的问题:
给你个函数 \(f(x)\),若对于实数 \(m\),\(f(x)=m\) 有两个不同的根 \(x_1,x_2\),此时求证一个关于 \(x_1,x_2,m\) 的不等式。
增强函数大概使用这样的方法:
- 将不等式转换为左右同构,即 \(g(x_1)<g(x_2)\) 的形式,并且要求 \(g\) 的极值点与 \(f\) 相同。
- 构造一个简单的函数 \(h\) 使得 \(F(x)=h(f(x))+g(x)\) 单调。
- 不妨 \(F\) 递增,通过 \(F(x_1)<F(x_2)\) 两边同时减去 \(h(f(x_1))\) 得 \(g(x_1)<g(x_2)\) 得证。
这个 \(F\) 在文中被称作增强函数,我觉得很有道理。
例
更具体,举个例子:
(2021·新高考I卷)\(f(x)=x\ln x-x=m\) 两根 \(x_1,x_2\),证明 \(x_1+x_2>2\)。
即要证:
\[\begin{aligned} (x_1+x_2)(x_2-x_1)&>2(x_2-x_1)\\ g(x_2)=x_2^2-2x_2&>x_1^2-2x_1=g(x_1) \end{aligned} \]构造 \(F(x)=-2f(x)+g(x)=-2x\ln x+x^2\),有 \(F'(x)=2x-2-2\ln x>0\),即 \(F(x)\) 递增。
则 \(F(x_1)<F(x_2)\),即 \(-2f(x_1)+g(x_1)<-2f(x_2)+g(x_2)\),\(g(x_2)>g(x_1)\),得证。
更多的例子建议在原文中找,不赘述。
机械化的构造方式
不妨 \(f,g\) 极值点均为 \(x_0\),思考如何构造出满足条件的 \(F\)。
\(g\) 的极值点与 \(f\) 相同,只能赌一手需要证的东西只在 \(x_0\) 取等,否则我不会做。
\(F\) 单调,而 \(f,g\) 极值点都位于 \(x_0\),\(F'(x_0)=f'(x_0)h'(f(x_0))+g'(x_0)=0\),\(F\) 极值点也为 \(x_0\),同时 \(F\) 需要单调,也就是说 \(x_0\) 既是 \(F'\) 的极值点,也是 \(F'\) 的零点。
想到用 \(F''(x_0)=0\) 来刻画,但这并不充分,原因是 \(F'\) 可能分居 \(x\) 轴两侧,但恰好在 \(x_0\) 处斜率为 \(0\),如图。
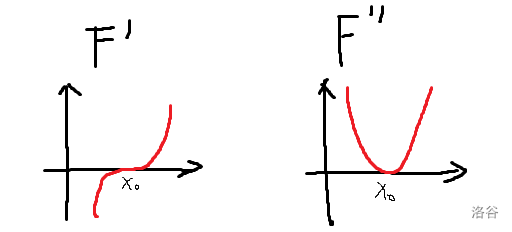
为了杜绝这种反例的出现,使用 \(F'''(x_0)\neq 0\) 来判定,但这并不必要,原因依葫芦画瓢自己脑补,故使用 \(F''''(x_0)= 0\) 来修正,然后套娃下去。(这个稍微有点感性理解,但我不知道咋说)
所以 \(F\) 需要满足的其实是:最小的满足 \(f^{(k)}(x_0)\neq0\) 的 \(\ge 2\) 的正整数 \(k\) 是奇数。这个条件是必要的。
说明这个条件的充分性:将 \(F\) 在 \(x_0\) 处泰勒展开,不妨第 \(i\) 项系数数 \(a_i\),则 \(F(x_0)=a_0\), \(F(x_0+dx)=a_0+a_kdx^k+o\left(dx^k\right)\),\(F(x_0-dx)=a_0+a_k(-dx)^k+o\left((-dx)^k\right)\),常数项相减消掉,两式两边都除以 \(dx^k\),而 \(k\) 为奇数正负变号,说明 \(F\) 在 \(x_0\) 处是单调的。
所以机械化的构造方式就呼之欲出了,将 \(f,g\) 在 \(x_0\) 处泰勒展开,然后用 \(f\) 消去 \(g\) 的偶数次项。这样构造出的 \(h\) 是一个次数有限的多项式函数(若 \(h\) 次数并不是有限的,感性理解 \(F\) 会变成常函数)。原文中 \(f(x)=x-\ln x=m\Rightarrow x_1+x_2<\dfrac{4a+2}{3}\) 便是一个 \(h(x)\neq kx\) 的例子。
好了,除开比较诡异的边界情况不想讨论,现在这种方法也变成重复性劳动了。
标签:增强,函数,ln,2x,构造,dx,极值 From: https://www.cnblogs.com/ustze/p/17033900.html