单调队列
前言
图床在 \(Github\) 中 ,如果访问不了 \(Github\) ,则图片无法加载
引入
原题链接:P1886 滑动窗口 /【模板】单调队列 - 洛谷
题意简述:有一个长度为 \(n\) 的数组,求其每 \(k\) 个连续的数中的最大值及最小值。
常规思路,对于每一段 \(i\sim i+k-1\) 的序列,逐个比较来找出最大值(和最小值),时间复杂度约为 \(O(n \times k)\)。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// n=7,k=4,a={1,3,6,2,5,1,7};
int n = sc.nextInt(), k = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; ++i) {
a[i] = sc.nextInt();
}
for (int i = 0; i + k - 1 < n; ++i) {
int max = a[i], min = a[i];
for (int j = 1; j < k; ++j) {
max = Math.max(max, a[i + j]);
min = Math.min(min, a[i + j]);
}
System.out.println(String.format("从%d开始的k个数中最大值为:%d,最小值为:%d", i, max, min));
}
}
}
很显然,这其中进行了大量重复工作,除了开头 \(k-1\) 个和结尾 \(k-1\) 个数之外,每个数都进行了 \(k\) 次比较,而题中 \(100\%\) 的数据为 \(n\leq 10^6\) ,当 \(k\) 稍大的情况下,显然会 \(TLE\)。
定义
顾名思义,单调队列的重点分为「单调」和「队列」。
-
「单调」指的是元素的「规律」——递增(或递减)。
-
「队列」指的是元素只能从队头和队尾进行操作(是一个双端队列)。
基本思想
维护一个双端队列(\(Deque\)),遍历序列,当且仅当一个元素可能为某个区间的最值时才保留他。
例题分析
以求连续的 \(k\) 个数的最大值为例。
若 \(n=7,k=4,arr=\{1,3,6,2,5,1,7\}\)。
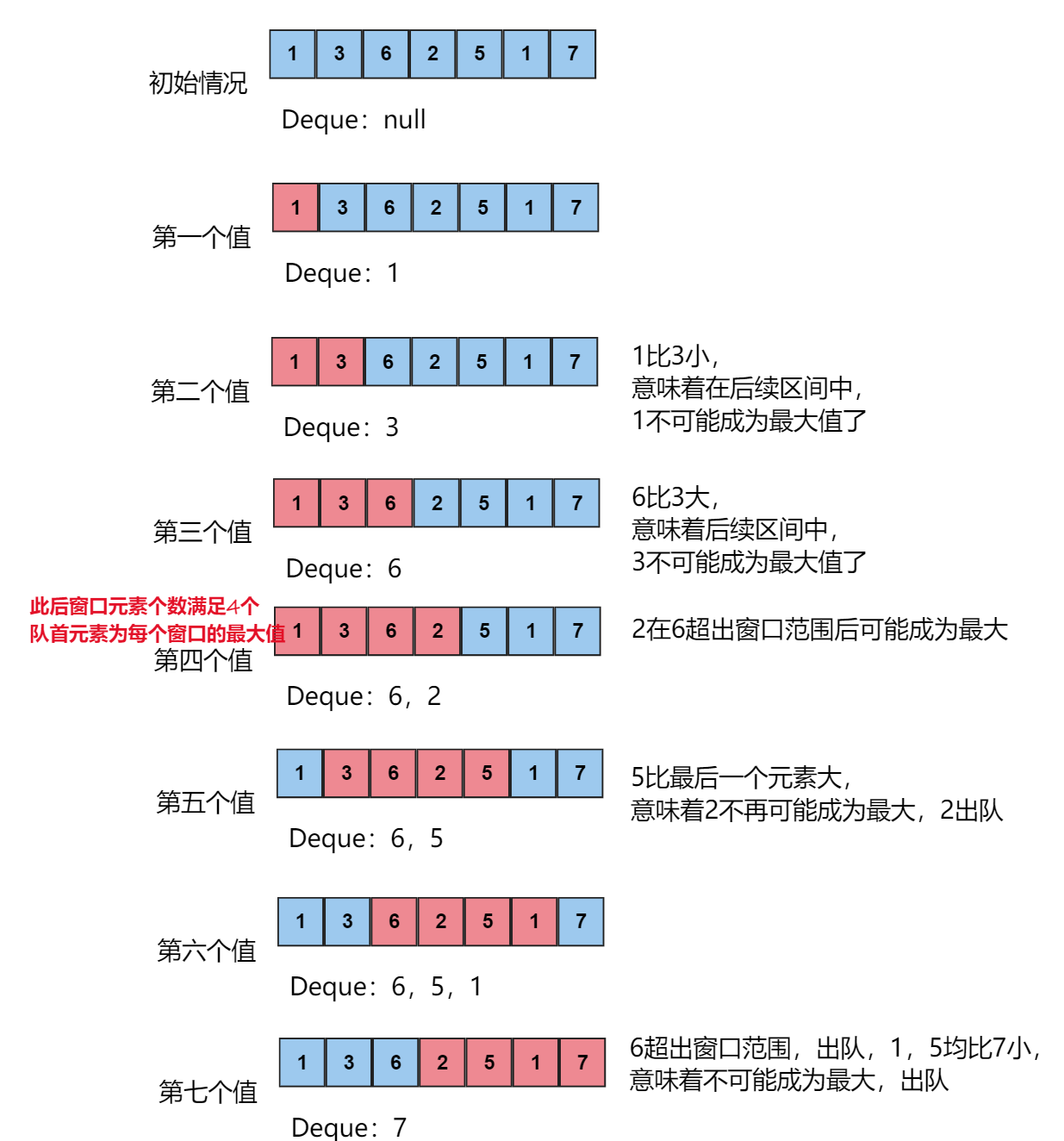
import java.io.*;
import java.util.ArrayDeque;
import java.util.Deque;
public class Main {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static PrintWriter out=new PrintWriter(System.out);
static int get() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
final int n = get(), k = get();
int[] a = new int[n];
for (int i = 0; i < n; ++i) a[i] = get();
Deque<Integer> min = new ArrayDeque<>(), max = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
//如果超出窗口范围
if (!min.isEmpty() && i - min.peekFirst() + 1 > k) min.pollFirst();
//如果不再可能成为最小值,则出队
while (!min.isEmpty() && a[min.peekLast()] >= a[i]) min.pollLast();
min.offerLast(i);
//说明此时窗口内元素个数已经足够,此后每个队首元素均为对应窗口的最值
if (i + 1 >= k) out.print(a[min.peekFirst()] + " ");
}
out.println();
for (int i = 0; i < n; ++i) {
//最大值同理
if (!max.isEmpty() && i - max.peekFirst() + 1 > k) max.pollFirst();
while (!max.isEmpty() && a[max.peekLast()] <= a[i]) max.pollLast();
max.offerLast(i);
if (i + 1 >= k) out.print(a[max.peekFirst()] + " ");
}
out.close();
}
}