标签：AtCoder int 题解 bmod ret choose 251 void define

AtCoder Beginner Contest 251 Solution

目录

• AtCoder Beginner Contest 251 Solution
  • 更好的阅读体验戳此进入
  • 题面链接
  • 题面 Luogu 链接
  • 老样子abc太水了就跳了
  • [ABC251D] At Most 3 (Contestant ver.)
    • 题面
    • Solution
    • Code
  • [ABC251E] Takahashi and Animals
    • 题面
    • Solution
    • Code
  • [ABC251F] Two Spanning Trees
    • 题面
    • Solution
    • Code
  • G 是计算几何，暂时跳了，以后有机会再回来做
  • [ABC251Ex] Fill Triangle
    • 题面
    • Solution
    • Code
  • UPD

更好的阅读体验戳此进入

题面链接

题面 Luogu 链接

老样子abc太水了就跳了

[ABC251D] At Most 3 (Contestant ver.)

题面

给你整数 \(W(1 \le W \le 10^6)\)。 你必须构造一个数组 \(a\)，包含最多 \(300\) 个元素，使得小于等于 \(W\) 的所有正整数都可以被 \(a\) 数组的元素相加表示出来。

Solution

显然按照十进制拆分成三组即可，即 $ [1, 99], [100, 9900], [10000, 990000] $ 即可，共 $ 99 \times 3 = 297 $ 个。

Code

#define _USE_MATH_DEFINES
#include <bits/stdc++.h>

#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}

using namespace std;

mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}

typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;

template < typename T = int > 
inline T read(void);

int main(){
    printf("297\n");
    for(int i = 1; i <= 99; ++i)printf("%d %d %d ", i, i * 100, i * 10000);
    printf("\n");
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

template < typename T >
inline T read(void){
    T ret(0);
    int flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

[ABC251E] Takahashi and Animals

题面

有 \(n\) 只动物围成一圈，你可以花费 \(a[i]\) 喂食动物 \(i\) 和 \(i+1\)。特别地，你可以花费 \(a[n]\) 喂食动物 \(n\) 和 \(1\)。

输出喂食所有动物需要的最小花费。

Solution

DP 显然，令 $ dp(i, 0/1) $ 表示考虑前 $ i $ 个元素且最后一个元素不喂 / 喂的最小花费。转移显然，注意要考虑一下 $ N $ 和 $ 1 $ 之间，具体选择哪个即可。

Code

#define _USE_MATH_DEFINES
#include <bits/stdc++.h>

#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}

using namespace std;

mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}

typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;

template < typename T = int >
inline T read(void);

int N;
int a[310000];
ll dp[310000][2];

int main(){
    N = read();
    for(int i = 1; i <= N; ++i)a[i] = read();
    memset(dp, 0x3f, sizeof dp);
    dp[1][1] = a[1];
    for(int i = 2; i <= N; ++i)
        dp[i][0] = dp[i - 1][1],
        dp[i][1] = min(dp[i - 1][1], dp[i - 1][0]) + a[i];
    // for(int i = 1; i <= N; ++i)printf("%d: 0 = %lld, 1 = %lld\n", i, dp[i][0], dp[i][1]);
    ll ans = min(dp[N][1], dp[N][0]);
    dp[1][0] = 0;
    for(int i = 2; i <= N; ++i)
        dp[i][0] = dp[i - 1][1],
        dp[i][1] = min(dp[i - 1][1], dp[i - 1][0]) + a[i];
    ans = min(ans, dp[N][1]);
    printf("%lld\n", ans);
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

template < typename T >
inline T read(void){
    T ret(0);
    int flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

[ABC251F] Two Spanning Trees

题面

给定无向连通简单图，求其两个以 $ 1 $ 为根的生成树 $ T_1, T_2 $，满足：

• 对于 $ T_1 $，其任意一条非树边连结的两个节点均存在祖先关系，即一个点为另一个点的祖先。
• 对于 $ T_2 $，其任意一条非树边连结的两个节点均不存在祖先关系。

Solution

前者对图 DFS，后者对图 BFS，证明显然。

Code

#define _USE_MATH_DEFINES
#include <bits/stdc++.h>

#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}

using namespace std;

mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}

typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;

template < typename T = int >
inline T read(void);

struct Edge{
    Edge* nxt;
    int to;
    OPNEW;
}ed[410000];
ROPNEW(ed);
Edge* head[410000];

int N, M;
bool vis[210000];

void dfs(int p = 1){
    vis[p] = true;
    for(auto i = head[p]; i; i = i->nxt){
        if(vis[SON])continue;
        printf("%d %d\n", p, SON);
        dfs(SON);
    }
}
void bfs(void){
    memset(vis, false, sizeof vis);
    queue < int > cur;
    cur.push(1), vis[1] = true;
    while(!cur.empty()){
        int tp = cur.front(); cur.pop();
        for(auto i = head[tp]; i; i = i->nxt){
            if(vis[SON])continue;
            printf("%d %d\n", tp, SON);
            vis[SON] = true, cur.push(SON);
        }
    }
}

int main(){
    N = read(), M = read();
    for(int i = 1; i <= M; ++i){
        int s = read(), t = read();
        head[s] = new Edge{head[s], t};
        head[t] = new Edge{head[t], s};
    }dfs(), bfs();
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

template < typename T >
inline T read(void){
    T ret(0);
    int flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

G 是计算几何，暂时跳了，以后有机会再回来做

[ABC251Ex] Fill Triangle

题面

存在序列 $ a_n $，将其压缩后给定。具体地，给定序列 $ P $ 以如下形式：$ ((a_1, c_1), (a_2, c_2), \cdots, (a_m, c_m)) $，表示序列 $ a $ 中有 $ c_1 $ 个 $ a_1 \(，\) c_2 $ 个 $ a_2 $，以此类推，且按序拼接。令序列 $ a_n $ 为三角金字塔 $ B $ 的第 $ n $ 层，即 $ B(n, i) = a_i $。特别地，该三角金字塔的递推式为 $ B(i, j) = (B(i + 1, j) + B(i + 1, j + 1)) \bmod{7} $。给定 $ k $，求该三角金字塔第 $ k $ 层的序列。

Solution

首先可以尝试随意给定一个序列 $ a_n $ 并打表，或手推一下，假设 $ n = 5 $，有：

$ a_1 + 4a_2 + 6a_3 + 4a_4 + a_5 $
$ a_1 + 3a_2 + 3a_3 + a_4 $	$ a_2 + 3a_3 + 3a_4 + a_5 $
$ a_1 + 2a_2 + a_3 $	$ a_2 + 2a_3 + a_4 $	$ a_3 + 2a_4 + a_5 $
$ a_1 + a_2 $	$ a_2 + a_3 $	$ a_3 + a_4 $	$ a_4 + a_5 $
$ a_1 $	$ a_2 $	$ a_3 $	$ a_4 $	$ a_5 $

不难发现这玩意每一项实际上就是二项式系数，或者说杨辉三角。并且还能发现，对于每一行的元素，它们的系数均相同，不同的只是将下标整体向右平移了一位。

此时我们便可以根据这个性质，求出对于第 $ k $ 层，第 $ x $ 列的元素，有：

\[B(k, x) = \sum_{i = 0}^{n - k}{n - k \choose i} a_{x + i} \bmod{7} \]

显然我们想要算出 $ k $ 层的所有元素，但是直接套这个式子暴力算是肯定过不了的。考虑优化。

显然序列 $ a $ 是由一段一段的相同元素构成的，而我们的查询就是在 $ a $ 里的查询一个区间然后按序将组合数乘上去。当我们从 $ B(k, x) $ 到 $ B(k, x + 1) $ 的时候，通过我们之前的结论可知需要将下标向右平移一位，而所有组合数的值不变，大概的过程如图：

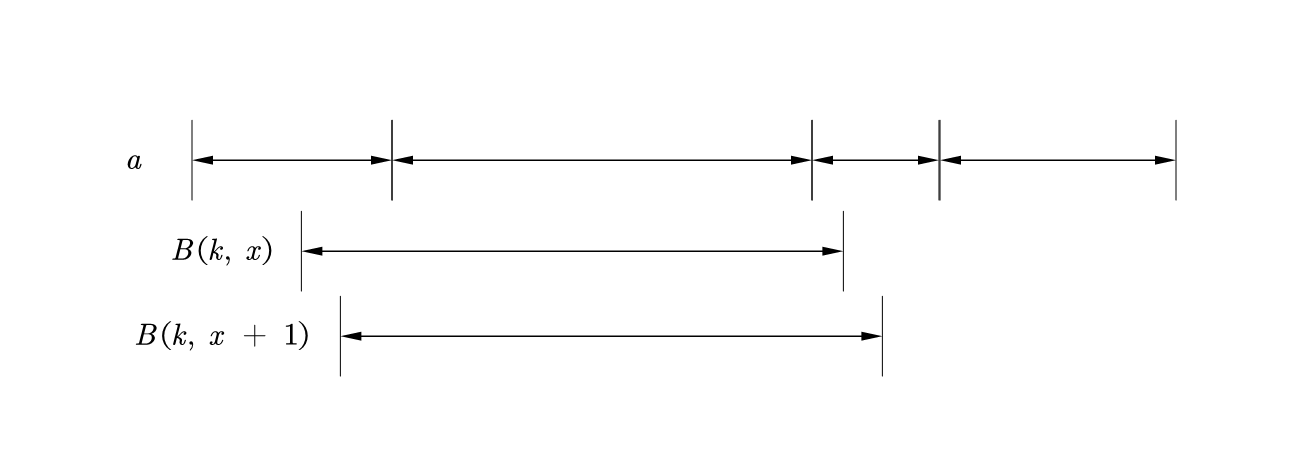
观察发现，这个东西平移之后，对于大多数的 $ {n - k \choose i} \times a_{x + i} $ 变成 $ {n - k \choose i} \times a_{x + i + 1} $，都存在 $ a_{x + i} = a_{x + i + 1} $，而对于这些的贡献是完全不变的。不难想到这个变化操作的复杂度最多是 $ O(m) $ 的。所以当我们确定了 $ B(k, 1) $ 之后，后面的 $ B(k, 2) $ 到 $ B(k, k) $ 就都可以每次 $ O(m) $ 求解，故这步的复杂度优化为 $ O(mk) $。

具体地当我们移动询问区间的时候，遍历所有段，如果某一段的右端点在当前区间内，那么显然指向这一段的组合数会移动到下一段中，所以需要减掉前面的加上现在的。注意移动这步实际上是 $ O(mk \log n) $ 的，而且这只 $ \log $ 不小，所以会 TLE，则我们考虑预处理 Lucas。显然直接预处理 $ 10^9 $ 范围肯定不行，于是这里有个高妙的思路，我们本身的模数为 $ 7 $，那么我们可以先让值对 $ 7^k $ 取模，然后再对 $ 7 $ 取模，这个显然是等价的。而如果我们搞一个 $ 10^5 $ 左右的 $ 7^k $ 的话，那么一步 Lucas 之后需要求的组合数就都在 $ 10^5 $ 以内了，所以这个时候我们只需要预处理 $ 10^5 $ 以内的组合数，那么对于每次求 Lucas 直接拆一次但是不递归，直接查值乘起来取模即可，这样复杂度就是 $ O(1) $ 了，或者说 $ O(2) $，于是复杂度会变成 $ O(mk) $。同时不难发现，存在 $ $

于是现在的问题就仅剩如何求 $ B(k, 1) $，也就是求：

\[\sum_{i = 0}^{n - k}{n - k \choose i} a_{i + 1} \bmod{7} \]

首先还是考虑之前的思路，一定会有很多段的相同的 $ a $，假设我们存在一段 $ [l, r] $ 满足 $ \forall i \in [l, r), a_i = a_{i + 1} $，那么显然此处的值即为：

\[\sum_{i = l - 1}^{r - 1}{n - k \choose i}a_{i + 1} \bmod{7} \]

所以这个东西显然需要快速处理一段组合数，可以考虑做一个组合数的前缀和，这样即可 $ O(1) $ 查询一段组合数的求和，然后乘上 $ a_l $ 即可，这样每次的复杂度也就是 $ O(m) $ 了。当然我们肯定不能对于 $ n - k $ 以内的每个数求前缀和，所以可以对 $ m $ 段相同的分别求出对应的前缀和，然后查询即可。求的时候前面段的直接求和，最后剩下的不足一段的单独计算即可。

于是现在问题再次转化为如何快速求这种形式的组合数前缀和，可以参考该题：LG-P4345 [SHOI2015]超能粒子炮·改。

具体地，对于求 $ F(n, k) = \sum_{i = 0}^k {n \choose i} \bmod p $，且 $ p $ 为质数，可以尝试通过 Lucas 进行处理（后面的式子最终都需要取模，这里省略）：

\[\begin{aligned} \sum_{i = 0}^k {n \choose i} \bmod p &= \sum_{i = 0}^k {\lfloor \dfrac{n}{p} \rfloor \choose \lfloor \dfrac{i}{p} \rfloor} \times {n \bmod{p} \choose i \bmod{p}} \end{aligned} \]

然后发现对于前面的 $ \lfloor \dfrac{i}{p} \rfloor $，这个就是个数论分块，也可以按照这个思想，将原式化为：

\[{\lfloor \dfrac{n}{p} \rfloor \choose 0}\sum_{i = 0}^{p - 1} {n \bmod{p} \choose i \bmod{p}} + {\lfloor \dfrac{n}{p} \rfloor \choose 1}\sum_{i = 0}^{p - 1} {n \bmod{p} \choose i \bmod{p}} + \cdots + {\lfloor \dfrac{n}{p} \rfloor \choose \lfloor \dfrac{k}{p} \rfloor - 1}\sum_{i = 0}^{p - 1} {n \bmod{p} \choose i \bmod{p}} + {\lfloor \dfrac{n}{p} \rfloor \choose \lfloor \dfrac{k}{p} \rfloor}\sum_{i = 0}^{k \bmod{p}} {n \bmod{p} \choose i \bmod{p}} \]

然后继续转化：

\[\sum_{i = 0}^{p - 1} {n \bmod{p} \choose i \bmod{p}} \times \sum_{i = 0}^{\lfloor \dfrac{k}{p} \rfloor - 1}{\lfloor \dfrac{n}{p} \rfloor \choose i} + {\lfloor \dfrac{n}{p} \rfloor \choose \lfloor \dfrac{k}{p} \rfloor}\sum_{i =0}^{k \bmod{p}} {n \bmod{p} \choose i \bmod{p}} \]

此时对比我们之前设的 $ F(n, k) = \sum_{i = 0}^k {n \choose i} \bmod p $，所以原式可以再次化为：

\[F(n \bmod{p}, p - 1) \times F(\lfloor \dfrac{n}{p} \rfloor, \lfloor \dfrac{k}{p} \rfloor - 1) + {\lfloor \dfrac{n}{p} \rfloor \choose \lfloor \dfrac{k}{p} \rfloor} \times F(n \bmod{p}, k \bmod{p}) \]

然后我们只要随便与处理一下 $ p $ 以内的 $ F $，这样 $ F(n \bmod{p}, p - 1) $ 和 $ F(n \bmod{p}, k \bmod{p}) $ 即可 $ O(1) $ 查表，然后组合数直接用 Lucas 暴力算一下即可，对于 $ F(\lfloor \dfrac{n}{p} \rfloor, \lfloor \dfrac{k}{p} \rfloor - 1) $ 递归下去即可。

考虑这个东西的复杂度，用主定理推导一下即可：

\[T(n) = T(\lfloor \dfrac{n}{p} \rfloor) + f(n) \]

$ O(n) $ 处理一下组合数，则 $ f(n) $ 的复杂度只有 Lucas 的一只 $ \log $，所以最终这里单次求解的复杂度为 $ O(\log^2 n) $，然后我们要处理 $ m $ 个，则最终这步的复杂度为 $ O(m \log^2 n) $。最终复杂度为 $ O(mk + m \log^2 n + k \log n) $，显然能过。

至此我们就终于完成了这道题。

Code

#define _USE_MATH_DEFINES
#include <bits/stdc++.h>

#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}

using namespace std;

mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}

typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;

#define MOD (7)
#define SPL (117649) //7^6

template < typename T = int >
inline T read(void);

int f[10][10];
int N, M, K;
int origin(0);
int sumf[210];
int lucas_div[SPL + 10], lucas_mod[SPL + 10];
struct Blk{int l, r; int val;} blk[210];

int qpow(int a, int b){
    int ret(1), mul(a);
    while(b){
        if(b & 1)ret = ret * mul % MOD;
        b >>= 1;
        mul = mul * mul % MOD;
    }return ret;
}
int fact[10], inv[10];
void Init(void){
    fact[0] = 1;
    for(int i = 1; i < MOD; ++i)fact[i] = fact[i - 1] * i % MOD;
    inv[MOD - 1] = qpow(fact[MOD - 1], MOD - 2);
    for(int i = MOD - 2; i >= 0; --i)inv[i] = inv[i + 1] * (i + 1) % MOD;
}
int GetC(int n, int m){
    if(n < m)return 0;
    return fact[n] * inv[m] % MOD * inv[n - m] % MOD;
}
int Lucas(ll n, ll m){
    if(n < MOD && m < MOD)return GetC(n, m);
    return Lucas(n / MOD, m / MOD) * GetC(n % MOD, m % MOD) % MOD;
}
int O1Lucas(ll m){
    return (lucas_div[m / SPL] * lucas_mod[m % SPL]) % MOD;
}
void InitF(void){
    for(int i = 0; i <= MOD - 1; ++i)f[i][0] = f[0][i] = 1;
    for(int i = 1; i <= MOD - 1; ++i)
        for(int j = 1; j <= MOD - 1; ++j)
            f[i][j] = (f[i][j - 1] + Lucas(i, j)) % MOD;
}
int F(ll n, ll k){
    if(n < 0 || k < 0)return 0;
    if(n < MOD && k < MOD)return f[n][k];
    return (f[n % MOD][MOD - 1] * F(n / MOD, k / MOD - 1) % MOD + Lucas(n / MOD, k / MOD) * f[n % MOD][k % MOD] % MOD) % MOD;
}

int main(){
    Init(), InitF();
    N = read(), M = read(), K = read();
    for(int i = 0; i <= SPL; ++i)lucas_div[i] = Lucas((N - K) / SPL, i), lucas_mod[i] = Lucas((N - K) % SPL, i);
    int curl(1);
    for(int i = 1; i <= M; ++i)blk[i].val = read(), blk[i].l = curl, blk[i - 1].r = blk[i].l - 1, curl += read();
    blk[M].r = N; int lim = N - K + 1;
    for(int i = 1; i <= M; ++i)
        sumf[i] = (F(N - K, blk[i].r - 1) - F(N - K, blk[i].l - 2) + MOD) % MOD;
    for(int i = 1; i <= M; ++i){
        int l = blk[i].l, r = blk[i].r;
        if(l > lim)break;
        if(r <= lim)(origin += sumf[i] * blk[i].val % MOD) %= MOD;
        else (origin += (F(N - K, lim - 1) - F(N - K, l - 2) + MOD) % MOD * blk[i].val % MOD) %= MOD;
    }printf("%d ", origin);
    int cl = 1, cr = lim;
    for(int i = 2; i <= K; ++i){
        for(int m = 1; m <= M; ++m){
            int r = blk[m].r;
            if(cl <= r && r <= cr)
                origin = (origin - O1Lucas(r - cl) * blk[m].val % MOD + O1Lucas(r - cl) * blk[m + 1].val % MOD + MOD) % MOD;
        }++cl, ++cr;
        printf("%d ", origin);
    }printf("\n");
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

template < typename T >
inline T read(void){
    T ret(0);
    int flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

UPD

update-2022_12_02 初稿

标签：AtCoder,int,题解,bmod,ret,choose,251,void,define
From： https://www.cnblogs.com/tsawke/p/17032761.html