总之,VAE 本身是一个生成模型,我们假设观测的某个变量 \(\mathbf{x}\)(比如数字 0~9 的各种图像)受到隐变量 \(\mathbf{z}\) 的影响,那么在得到分布后,只需要采样得到一个 \(\mathbf{z}\),我们就能得到一个 \(\mathbf{x}\)
参考 - Lil's blog
参考 - 科学空间
pytorch 实践
Autocoder is invented to reconstruct high-dimensional data using a neural network model. A nice byproduct is dimension reduction: the bottleneck layer captures a compressed latent encoding. Such a low-dimensional representation can be used as en embedding vector in various applications (i.e. search), help data compression, or reveal the underlying data generative factors.
Notation
| Symbol | Mean |
|---|---|
| \(\mathcal{D}\) | The dataset, \(\mathcal{D} = \{ \mathbf{x}^{(1)}, \mathbf{x}^{(2)}, \dots, \mathbf{x}^{(n)} \}\) , contains \(n\) data samples; \(\vert\mathcal{D}\vert =n\). |
| \(\mathbf{x}^{(i)}\) | Each data point is a vector of \(d\) dimensions, \(\mathbf{x}^{(i)} = [x^{(i)}_1, x^{(i)}_2, \dots, x^{(i)}_d]\). |
| \(\mathbf{x}\) | One data sample from the dataset, \(\mathbf{x} \in \mathcal{D}\). |
| \(\mathbf{x}'\) | The reconstructed version of \(\mathbf{x}\). |
| \(\tilde{\mathbf{x}}\) | The corrupted version of \(\mathbf{x}\). |
| \(\mathbf{z}\) | The compressed code learned in the bottleneck layer. |
| \(a_j^{(l)}\) | The activation function for the \(j\)-th neuron in the \(l\)-th hidden layer. |
| \(g_{\phi}(.)\) | The encoding function parameterized by \(\phi\). |
| \(f_{\theta}(.)\) | The decoding function parameterized by \(\theta\). |
| \(q_{\phi}(\mathbf{z}\vert\mathbf{x})\) | Estimated posterior probability function, also known as probabilistic encoder. |
| \(p_{\theta}(\mathbf{x}\vert\mathbf{z})\) | Likelihood of generating true data sample given the latent code, also known as probabilistic decoder. |
Autoencoder
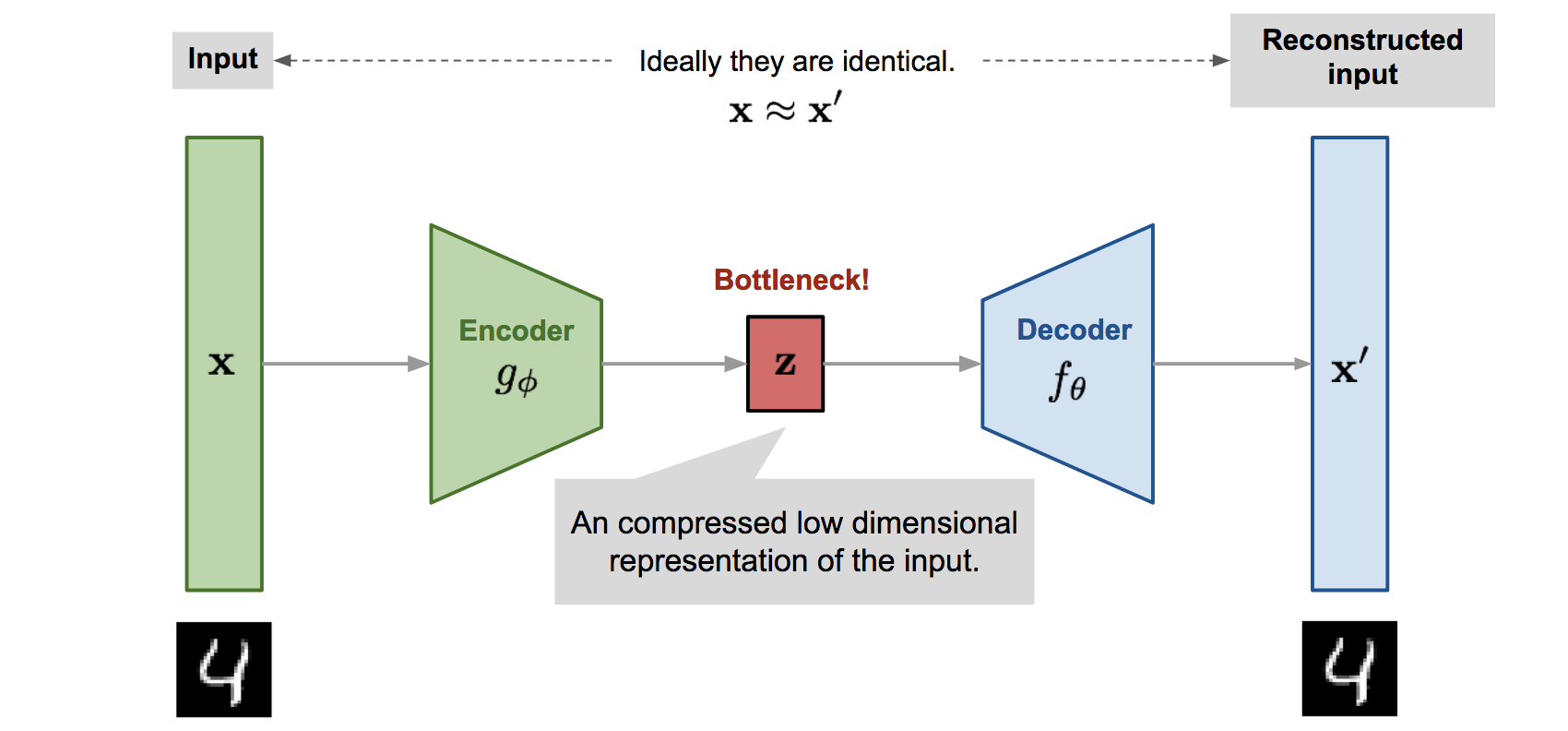
The model contains an encoder function \(g(.)\) parameterized by \(\phi\) and a decoder function \(f(.)\) parameterized by \(\theta\). The low-dimensional code learned for input \(\mathbf{x}\) in the bottleneck layer is \(\mathbf{z} = g_\phi(\mathbf{x})\) and the reconstructed input is \(\mathbf{x}' = f_\theta(g_\phi(\mathbf{x}))\).
The parameters \((\theta, \phi)\) are learned together to output a reconstructed data sample same as the original input, \(\mathbf{x} \approx f_\theta(g_\phi(\mathbf{x}))\), or in other words, to learn an identity function. A simple metric is MSE loss:
\[L_\text{AE}(\theta, \phi) = \frac{1}{n}\sum_{i=1}^n (\mathbf{x}^{(i)} - f_\theta(g_\phi(\mathbf{x}^{(i)})))^2 \]Denoising Autoencoder
To avoid overfitting and improve the robustness, Denoising Autoencoder (Vincent et al. 2008) proposed a modification to the basic autoencoder. The input is partially corrupted by adding noises to or masking some values of the input vector in a stochastic manner, \(\tilde{\mathbf{x}} \sim \mathcal{M}_\mathcal{D}(\tilde{\mathbf{x}} \vert \mathbf{x})\)
. Then the model is trained to recover the original input (note: not the corrupt one).
where \(\mathcal{M}_\mathcal{D}\) defines the mapping from the true data samples to the noisy or corrupted ones.
In the experiment of the original DAE paper, the noise is applied in this way: a fixed proportion of input dimensions are selected at random and their values are forced to 0.
VAE: Variational Autoencoder
Instead of mapping the input into a fixed vector, we want to map it into a distribution. Let’s label this distribution as \(p_\theta\), parameterized by \(\theta\). The relationship between the data input \(\mathbf{x}\) and the latent encoding vector \(\mathbf{z}\) can be fully defined by:
- Prior \(p_\theta(\mathbf{z})\),关于 \(\mathbf{z}\)
- Likelihood \(p_\theta(\mathbf{x}\vert\mathbf{z})\)
- Posterior \(p_\theta(\mathbf{z}\vert\mathbf{x})\)
如果知道分布参数 \(\theta^{*}\),我们可以通过对 \(p_{\theta^*}(\mathbf{z})\) 采样得到 \(\mathbf{z}\),再通过分布 \(p_{\theta^*}(\mathbf{x} \vert \mathbf{z})\) 得到一个接近真实数据的 \(\mathbf{x}\)
Assuming that we know the real parameter \(\theta^{*}\) for this distribution. In order to generate a sample that looks like a real data point \(\mathbf{x}^{(i)}\), we follow these steps:
- First, sample a \(\mathbf{z}^{(i)}\) from a prior distribution \(p_{\theta^*}(\mathbf{z})\).
- Then a value \(\mathbf{x}^{(i)}\) is generated from a conditional distribution \(p_{\theta^*}(\mathbf{x} \vert \mathbf{z} = \mathbf{z}^{(i)})\).
于是在给定样本集 \(\mathcal{D}\) 后,对于每个样本 \(\mathbf{x}^{(i)}\) 对应生成概率 \(p_\theta(\mathbf{x}^{(i)}) = \int p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}) p_\theta(\mathbf{z}) d\mathbf{z}\),而这个 \(\theta^{*}\) 应当是最大似然的:
The optimal parameter \(\theta^{*}\) is the one that maximizes the probability of generating real data samples:
\[\begin{aligned} \theta^{*} &= \arg\max_\theta \prod_{i=1}^n p_\theta(\mathbf{x}^{(i)}) \\ &= \arg\max_\theta \sum_{i=1}^n \log p_\theta(\mathbf{x}^{(i)}) \\ \end{aligned} \]where
\[p_\theta(\mathbf{x}^{(i)}) = \int p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}) p_\theta(\mathbf{z}) d\mathbf{z} \]不过这种计算方法并不好算,我们引入一个新的分布 \(q_\phi(\mathbf{z}\vert\mathbf{x})\),用来拟合 \(p_\theta(\mathbf{z}\vert\mathbf{x})\)
Unfortunately it is not easy to compute \(p_\theta(\mathbf{x}^{(i)})\) in this way, as it is very expensive to check all the possible values of \(\mathbf{z}\) and sum them up. To narrow down the value space to facilitate faster search, we would like to introduce a new approximation function to output what is a likely code given an input \(\mathbf{x}\), \(q_\phi(\mathbf{z}\vert\mathbf{x})\), parameterized by \(\phi\).
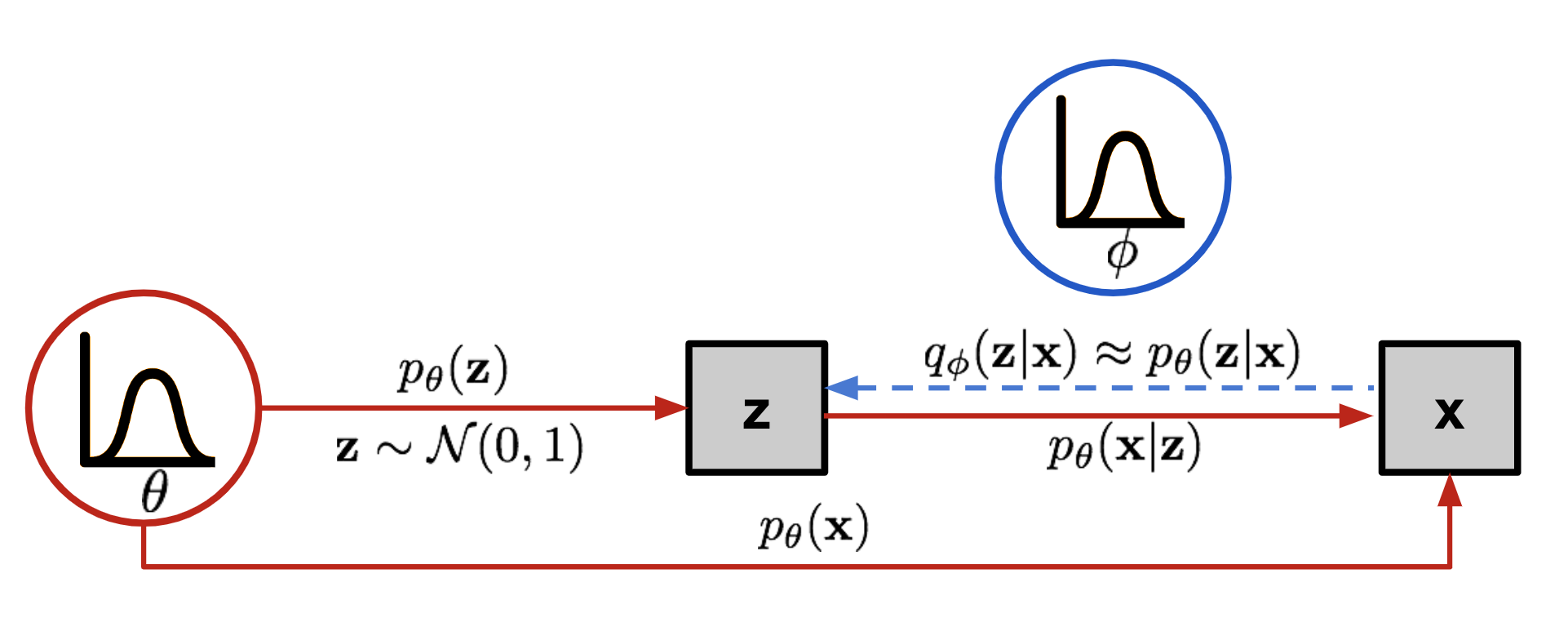
Now the structure looks a lot like an autoencoder:
- The conditional probability \(p_\theta(\mathbf{x} \vert \mathbf{z})\) defines a generative model, similar to the decoder \(f_\theta(\mathbf{x} \vert \mathbf{z})\) introduced above. \(p_\theta(\mathbf{x} \vert \mathbf{z})\) is also known as probabilistic decoder.
- The approximation function \(q_\phi(\mathbf{z} \vert \mathbf{x})\) is the probabilistic encoder, playing a similar role as \(g_\phi(\mathbf{z} \vert \mathbf{x})\) above.

Loss Function: ELBO, Evidence Lower Bound
引入一个新的分布 \(q_\phi(\mathbf{z}\vert\mathbf{x})\) 来拟合 \(p_\theta(\mathbf{z}\vert\mathbf{x})\),我们用 KL 散度来衡量两者的相似程度,可以推导得到下面的等式
We can use Kullback-Leibler divergence to quantify the distance between these two distributions, \(q_\phi(\mathbf{z}\vert\mathbf{x})\) and \(p_\theta(\mathbf{z}\vert\mathbf{x})\). Recall that KL divergence \(D_\text{KL}(X|Y)\) measures how much information is lost if the distribution Y is used to represent X.
In our case we want to minimize \(D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) | p_\theta(\mathbf{z}\vert\mathbf{x}) )\) with respect to \(\phi\).
Why use \(D_\text{KL}(q_\phi | p_\theta)\) (reversed KL) instead of \(D_\text{KL}(p_\theta | q_\phi)\) (forward KL):
首先注意到,以 $$D_\text{KL}\Big(p(x)\Big\Vert q(x)\Big) = \int p(x)\ln \frac{p(x)}{q(x)} dx=\mathbb{E}_{x\sim p(x)}\left[\ln \frac{p(x)}{q(x)}\right]$$ 为例,若 \(q(x)\) 在某个区域为零,而 \(p(x)\) 不为零,那么会出现 KL 散度无穷大的问题,换句话说,此时 \(q(x)\) 的非零区域是包含 \(p(x)\) 的
Forward KL divergence: \(D_\text{KL}(P|Q) = \mathbb{E}_{z\sim P(z)} \log\frac{P(z)}{Q(z)}\); we have to ensure that Q(z)>0 wherever P(z)>0. The optimized variational distribution \(q(z)\) has to cover over the entire \(p(z)\).
Reversed KL divergence: \(D_\text{KL}(Q|P) = \mathbb{E}_{z\sim Q(z)} \log\frac{Q(z)}{P(z)}\); minimizing the reversed KL divergence squeezes the \(Q(z)\) under \(P(z)\).
Let’s now expand the equation, so we have:
\[D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) =\log p_\theta(\mathbf{x}) + D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) - \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) \]Once rearrange the left and right hand side of the equation,
\[\log p_\theta(\mathbf{x}) - D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) = \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) - D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) \]等号左边第一项,就是似然取 log;第二项就是 KL 散度取负,我们自然希望等号两边越大越好;取负后,就可以作为代价函数 loss 使用
The LHS of the equation is exactly what we want to maximize when learning the true distributions: we want to maximize the (log-)likelihood of generating real data (that is \(\log p_\theta(\mathbf{x})\)) and also minimize the difference between the real and estimated posterior distributions (the term \(D_\text{KL}\) works like a regularizer). Note that \(p_\theta(\mathbf{x})\) is fixed with respect to \(q_\phi\).
So, the negation of the above defines our loss function:
\[\begin{aligned} L_\text{VAE}(\theta, \phi) &= -\log p_\theta(\mathbf{x}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) )\\ &= - \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})} \log p_\theta(\mathbf{x}\vert\mathbf{z}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}) ) \\ \theta^{*}, \phi^{*} &= \arg\min_{\theta, \phi} L_\text{VAE} \end{aligned} \]这里还有一个含义,当我们不断减小 loss 时,意味着似然的下界在增大
In Variational Bayesian methods, this loss function is known as the variational lower bound, or evidence lower bound. The “lower bound” part in the name comes from the fact that KL divergence is always non-negative and thus \(-L_\text{VAE}\) is the lower bound of \(\log p_\theta (\mathbf{x})\).
\[-L_\text{VAE} = \log p_\theta(\mathbf{x}) - D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) \leq \log p_\theta(\mathbf{x}) \]Therefore by minimizing the loss, we are maximizing the lower bound of the probability of generating real data samples.
Reparameterization Trick
回到代价函数:
\[L_\text{VAE}(\theta, \phi) = - \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})} \log p_\theta(\mathbf{x}\vert\mathbf{z}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}) ) \]分别考察两部分,前一部分求的是在 \(\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})\) 采样下的期望,但是采样是没法求导的,所以我们改写这个分布:\(\mathbf{z} = \mathcal{T}_\phi(\mathbf{x}, \boldsymbol{\epsilon})\),将随机的任务丢给 \(\boldsymbol{\epsilon}\)
The expectation term in the loss function invokes generating samples from \(\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})\). Sampling is a stochastic process and therefore we cannot backpropagate the gradient. To make it trainable, the reparameterization trick is introduced: It is often possible to express the random variable \(\mathbf{z}\) as a deterministic variable \(\mathbf{z} = \mathcal{T}_\phi(\mathbf{x}, \boldsymbol{\epsilon})\), where \(\boldsymbol{\epsilon}\) is an auxiliary (辅助的) independent random variable, and the transformation function \(\mathcal{T}_\phi\) parameterized by \(\phi\) converts \(\boldsymbol{\epsilon}\) to \(\mathbf{z}\) (将 \(\boldsymbol{\epsilon}\) 转化成 \(\mathbf{z}\)).
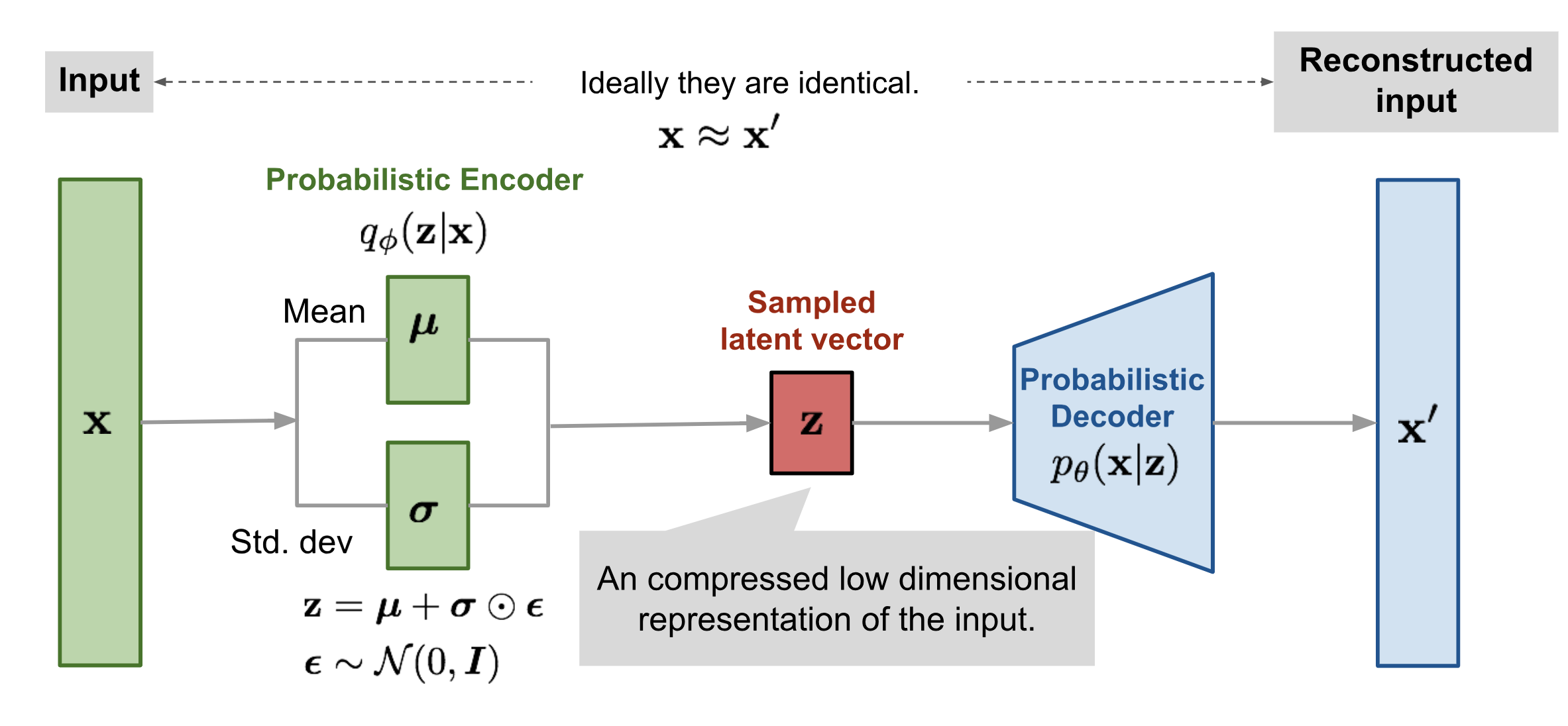
此外,我们不是要用 \(q_\phi(\mathbf{z}\vert\mathbf{x})\) 拟合嘛,我们得给一个形式,一般地我们选择用 多元高斯分布,而且为了方便我们假定这个高斯分布的协方差矩阵是对角阵,于是有 \(\mathbf{z} = \mathcal{T}_\phi(\mathbf{x}, \boldsymbol{\epsilon}) = \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon}\),其中 \(\boldsymbol{\mu}, \boldsymbol{\sigma}\) 是编码器学到的关于 \(\mathbf{x}\) 的输出
For example, a common choice of the form of \(q_\phi(\mathbf{z}\vert\mathbf{x})\) is a multivariate Gaussian with a diagonal covariance structure:
\[\begin{aligned} \mathbf{z} &\sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I}) & \\ \mathbf{z} &= \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon} \text{, where } \boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I}) & \scriptstyle{\text{; Reparameterization trick.}} \end{aligned} \]where \(\odot\) refers to element-wise product
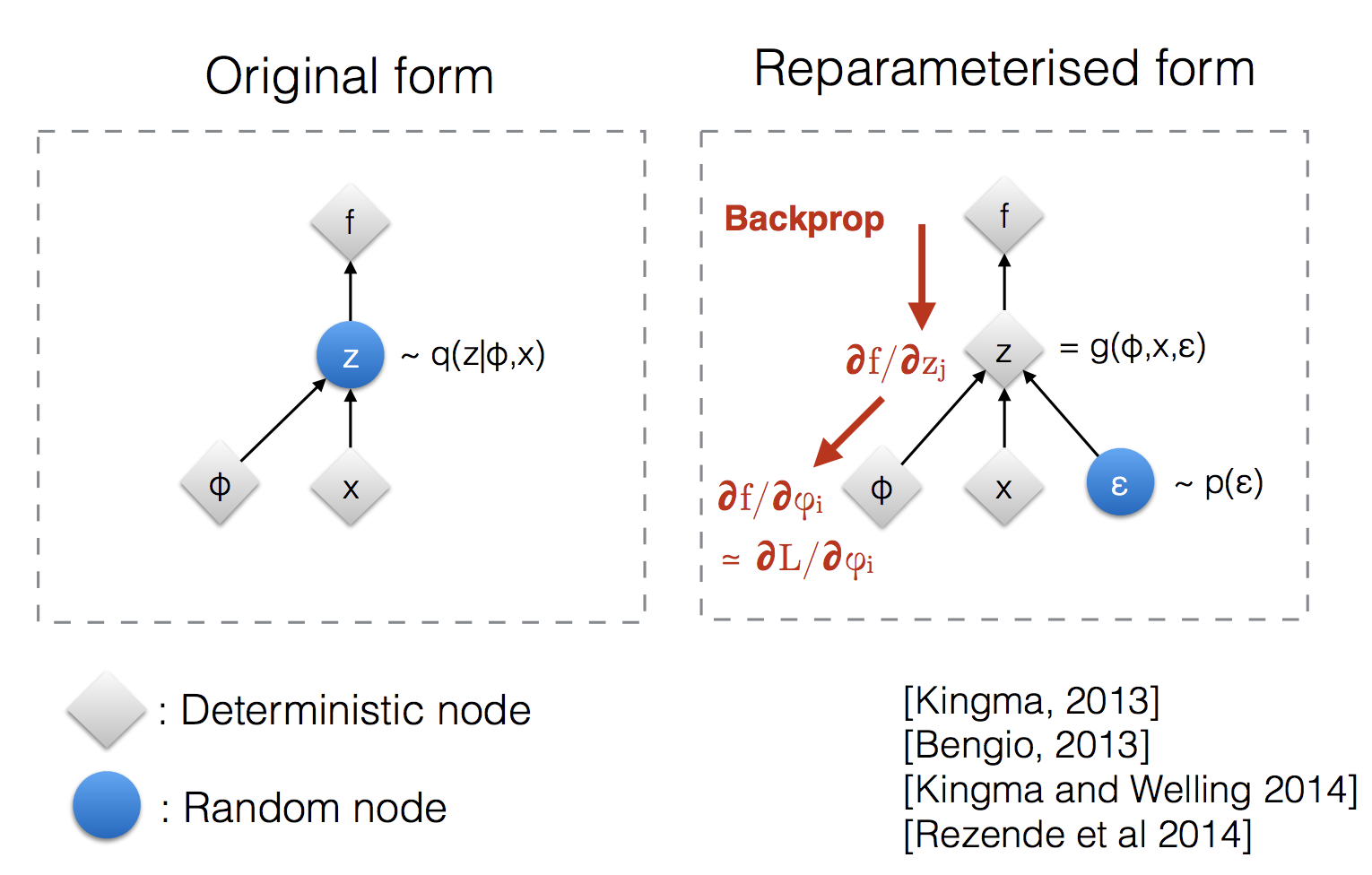
The reparameterization trick works for other types of distributions too, not only Gaussian. In the multivariate Gaussian case, we make the model trainable by learning the mean and variance of the distribution, \(\mu\) and \(\sigma\), explicitly using the reparameterization trick, while the stochasticity (随机性) remains in the random variable \(\boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I})\).
代价函数前半部分
于是,代价函数的第一项也就成了:
\[-\mathbb{E}_{\boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I})} \log p_\theta(\mathbf{x}\vert\mathbf{z} = \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon}) \]可是这又咋算?这时我才知道可以 采样计算,又即蒙特卡洛模拟的基础:
\[\mathbb{E}_{x\sim p(x)}[f(x)] = \int f(x)p(x)dx \approx \frac{1}{n}\sum_{i=1}^n f(x_i),\quad x_i\sim p(x) \]那么应该采样几个呢?VAE 给出的答案是:一个!
那么代价函数的第一项就成了:
为啥只要一次呢,事实上我们会运行多个 epoch,每次的隐变量都是随机生成的,因此当 epoch 数足够多时,事实上是可以保证采样的充分性的
代价函数后半部分
此外,我们还有代价函数的后半部分呢:\(D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}) )\)
其中 \(\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I})\) 是我们已经做好的,后者呢?我们直接认为,\(\mathbf{z}\) 服从标准正态分布,这样假设的原因是注意到 “任何 d 维分布都可以从一个 d 维高斯分布 + 一个足够复杂的函数映射得到”,足够复杂的函数已经用解码器做了
还有另一种理解,VAE 期望所有 \(q_\phi(\mathbf{z}\vert\mathbf{x})\),或者说 \(p_\theta(\mathbf{z}\vert\mathbf{x})\) 趋近于标准正态分布,那么就会有 \(\mathbf{z}\) 趋近正态分布,这样就能保证我们之后能通过在标准正态分布中采样 \(\mathbf{z}\) 来做生成了,所以令 \(p_\theta(\mathbf{z})\) 为标准正态做的 KL 散度,也是为了让 \(q_\phi(\mathbf{z}\vert\mathbf{x})\) 趋近正态分布的正则项
那么我们在做的就是求两个高斯分布的 KL 散度,有公式:
\[\begin{aligned} D_\text{KL}(\mathcal{N}(\boldsymbol{\mu_0}, \boldsymbol{\Sigma_0}) \| \mathcal{N}(\boldsymbol{\mu_1}, \boldsymbol{\Sigma_1})) &= \frac{1}{2}\bigg( \text{tr}(\boldsymbol{\Sigma_1}^{-1} \boldsymbol{\Sigma_0}) + (\boldsymbol{\mu_1}-\boldsymbol{\mu_0})^T\boldsymbol{\Sigma_1}^{-1}(\boldsymbol{\mu_1}-\boldsymbol{\mu_0}) - d + \log\frac{\det \boldsymbol{\Sigma_1}}{\det \boldsymbol{\Sigma_0}} \bigg) \\ &= \frac{1}{2}\bigg( \text{tr}(\boldsymbol{\sigma}^{2(i)}\boldsymbol{I}) + \boldsymbol{\mu}^{(i)T}\boldsymbol{\mu}^{(i)} - d - \log \det (\boldsymbol{\sigma}^{2(i)}\boldsymbol{I}) \bigg) & \text{; $\boldsymbol{\mu_0}=\boldsymbol{\mu}^{(i)}, \boldsymbol{\Sigma_0} = \boldsymbol{\sigma}^{2(i)}\boldsymbol{I}, \boldsymbol{\mu_1}=0, \boldsymbol{\Sigma_1} = \boldsymbol{I}$} \\ \end{aligned} \]以上,我们就完成力,我们最后的神经网络长下面这样
标签:编码器,mathbf,vert,Auto,boldsymbol,phi,VAE,theta,KL From: https://www.cnblogs.com/zhyh/p/17024514.html