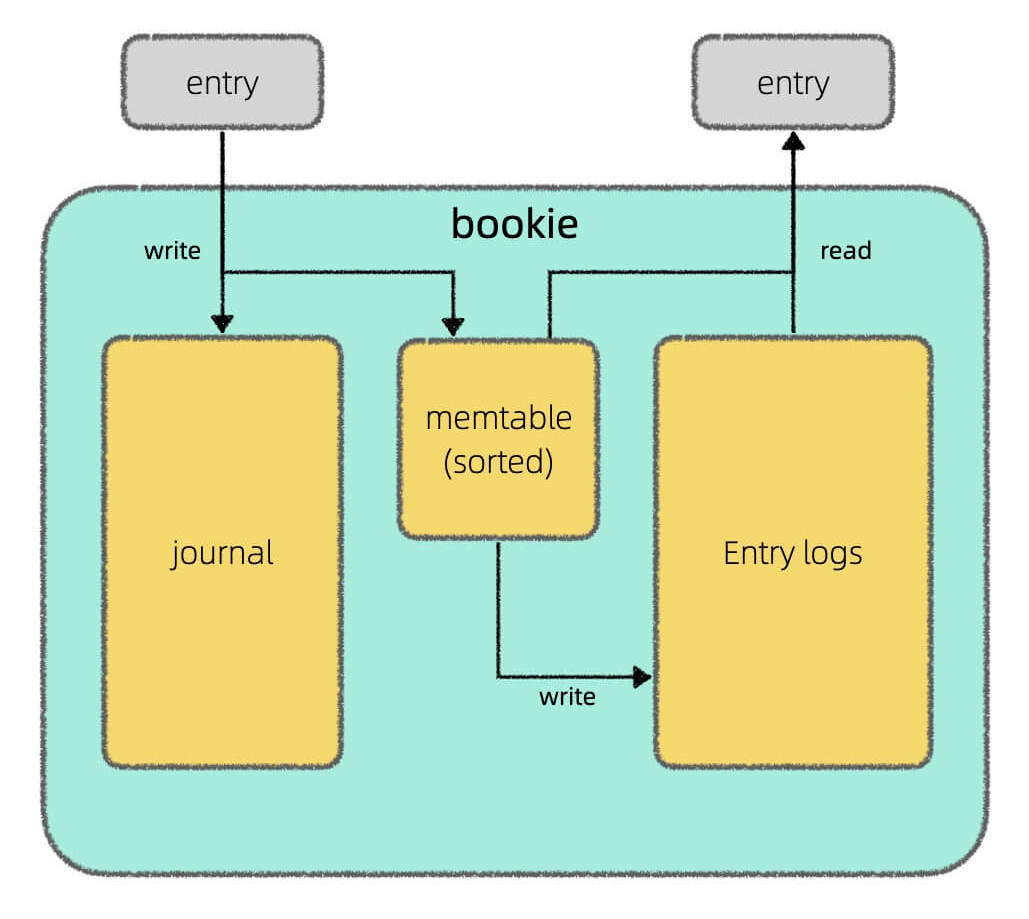
我在上篇文章 Apache Pulsar 的架构设计 中介绍了 Pulsar 存算分离的架构,其中 broker 只负责计算,由 BookKeeper 负责底层的存储,我还画了这样一张图说明 BookKeeper 读写分离的设计:
但是再深究下去,memtable具体是以怎样的格式持久化到磁盘上的呢?又是用什么算法高效查找一条消息的呢?
通过学习相关资料,我发现 Apache BookKeeper 底层存储引擎用的是 Facebook 开源的 RocksDB,而 RocksDB 又是基于 Google 开源的 LevelDB 改造的,而 LevelDB 的核心是一个叫做 LSM 树(Log Structured Merge Tree)的结构。
LevelDB 整个库的代码只有几百 KB,所以我去研究了 LSM 树的代码实现,总结了这篇文章,带你了解 LSM 树的设计原理。
什么是 LSM 树呢?如果说到 B+ 树大家应该不陌生,像 MySQL 这样的关系型数据库底层一般用 B+ 树结构来存储数据。LSM 树其实就是另一种存储数据的结构,常见于日志存储系统中。
首先,我们先来聊聊存储系统。
正如前文 学习数据结构和算法的框架思维 所说,一切数据结构从根本上讲都是增删查改,但在具体实现上,磁盘数据结构和内存数据结构会有比较大的差异。
内存数据结构你直接 new 一个出来就行了,不用关心这个结构在内存中是如何布局的,这些都由操作系统和编程语言代劳了。
但磁盘就不一样,考虑到计磁盘读取的操作效率相对比较低,且每次只能读取固定大小的磁盘数据,你要自己设计数据的存储布局,规定每个字节存什么信息,然后基于你设计的存储布局实现增删查改的 API,比较枯燥琐碎。
比如说,学过 MySQL 的话应该比较熟悉 B+ 树结构,但你肯定不容易看懂 B+ 树的代码。因为 B+ 树是磁盘数据结构,虽然原理上可以理解为 BST 的加强版,但考虑到数据文件格式的设计,真正的代码实现非常复杂。
所以一般来说,我们了解磁盘数据结构的原理,了解各个操作的时间复杂度就可以了,没必要特别纠结它的具体实现。
数据可变 vs 数据不可变
存储结构可以粗略分为两类:数据可变的和数据不可变的。所谓可变,就是说已经插入的数据还可以原地进行修改,不可变就是说已经插入的数据就不能再修改了。
B 树是数据可变的代表结构(B+ 树等衍生结构都归为 B 树一族)。你就想想 BST 吧,数据存在节点上,我们可以随意插入、删除、修改 BST 中的节点。
B 树的理论增删查改性能和 BST 一样都是 logN,但 B 树的实际写入效率并不是特别高:
一方面是因为 B 树需要分裂合并等操作保证整棵树的平衡性,这里面涉及很多磁盘随机读写的操作,性能会比较差;另一方面考虑到并发场景,修改 B 树结构时需要比较复杂的锁机制保证并发安全,也会一定程度影响效率。
综上,B 树的难点在于平衡性维护和并发控制,一般用在读多写少的场景。
LSM 树是数据不可变的代表结构。你只能在尾部追加新数据,不能修改之前已经插入的数据。
如果不能修改以前的数据,是不是就不能提供删、查、改的操作 API 呢?其实是可以的。
我们只需要提供set(key, val)和get(key)两个 API 即可。查询操作靠get(key),增删改操作都可以由set(key, val)实现:
如果set的key不存在就是新增键值对,如果已经存在,就是更新键值对;如果把val设置为一个特殊值(比如 null)就可以代表key被删掉了(墓碑机制)。
那么我对某个键key做了一系列操作后,我只要找到最近一次的操作,就能知道这个键当前的值是多少了。
从磁盘的角度来说,在尾部追加的写入效率非常高,因为不需要像 B 树那样维护复杂的树形结构嘛。但代价就是,查找效率肯定比较低,因为只能通过线性遍历去查找操作记录。
后面我会讲讲真正的 LSM 树如何针对读场景进行优化,但再怎么优化,肯定也达不到 B 树的读取效率。
同时,LSM 树还有一个明显弊端就是存在空间放大。在 B 树中一个键值对就占用一个节点,我更新这个键 100 次,它还是只占用一个节点。但在 LSM 树中,如果我更新一个键 100 次,就相当于写入了 100 条数据,会消耗更多空间。
后面会讲到,这个问题的解决方案是压实(compact),把操作序列中失效的历史操作消除掉,只保留最近的操作记录。
综上,LSM 树的难点在于 compact 操作和读取数据时的效率优化,一般用在写多读少的场景。
有序 vs 无序
可以说,存储结构的有序程度直接决定了该类结构的读写性能上限。有序度越高,读性能越强,但相应的,维护有序性的成本也越高,写入性能也就会越差。
你看 B 树,作为 BST 的加强版,实际上是维护了所有数据的有序性,读取性能必然起飞,但写入性能你也别抱太大希望。
LSM 树不可能向 B 树那样维护所有数据的有序性,但可以维护局部数据的有序性,从而一定程度提升读性能。
LSM 树的设计
就我的理解,LSM 树其实不是一种数据结构,而是一种存储方案。这里面涉及三个重要的数据组件:memtable,log,SSTable,正如我在 Apache Pulsar 的架构设计 中画的这幅图:

其中Journal就是log,Entry Log就是若干SSTable的集合,叫法不同罢了。
memtable是红黑树或者跳表这样的有序内存数据结构,起到缓存和排序的作用,把新写入的数据按照键的大小进行排序。当memtable到达一定大小之后,会被转化成SSTable格式刷入磁盘持久化存储。
SSTable(Sorted String Table)说白了就是一个特殊格式的文件,其中的数据按照键的大小排列,你可以把它类比成一个有序数组。而 LSM 树,说白了就是若干SSTable的集合。
log文件记录操作日志,在数据写入memtable的同时也会刷盘写入到log文件,作用是数据恢复。比如在memtable中的数据还没转化成SSTable持久化到磁盘时,如果突然断电,那么memtable里面的数据都会丢失,但有log文件在,就可以恢复这些数据。当然,等memtable中的数据成功转化成SSTable落盘之后,log文件中对应的操作日志就没必要存在了,可以被删除。
LSM 树的set写入过程并不复杂:写入log和memtable,最后转化成一个SSTable持久化到磁盘就行了。
最关键的应该是读取和 compact 的过程:SSTable要如何组织,才能快速get到一个key对应的val呢?如何定期对所有 SSTable 做 compact 瘦身呢?
其实有多种方案,其中比较常用的方案是按照层级组织SSTable:

图中每个绿色方块代表一个SSTable,若干个SSTable构成一层,总共有若干层,每层能够容纳的SSTable数量上限依次递增。
新刷入的SSTable在第 0 层,如果某一层的SSTable个数超过上限,则会触发 compact 操作,按照SSTable的键区间从该层和下一层选出若干SSTable合并成一个更大的SSTable,移动下一层:
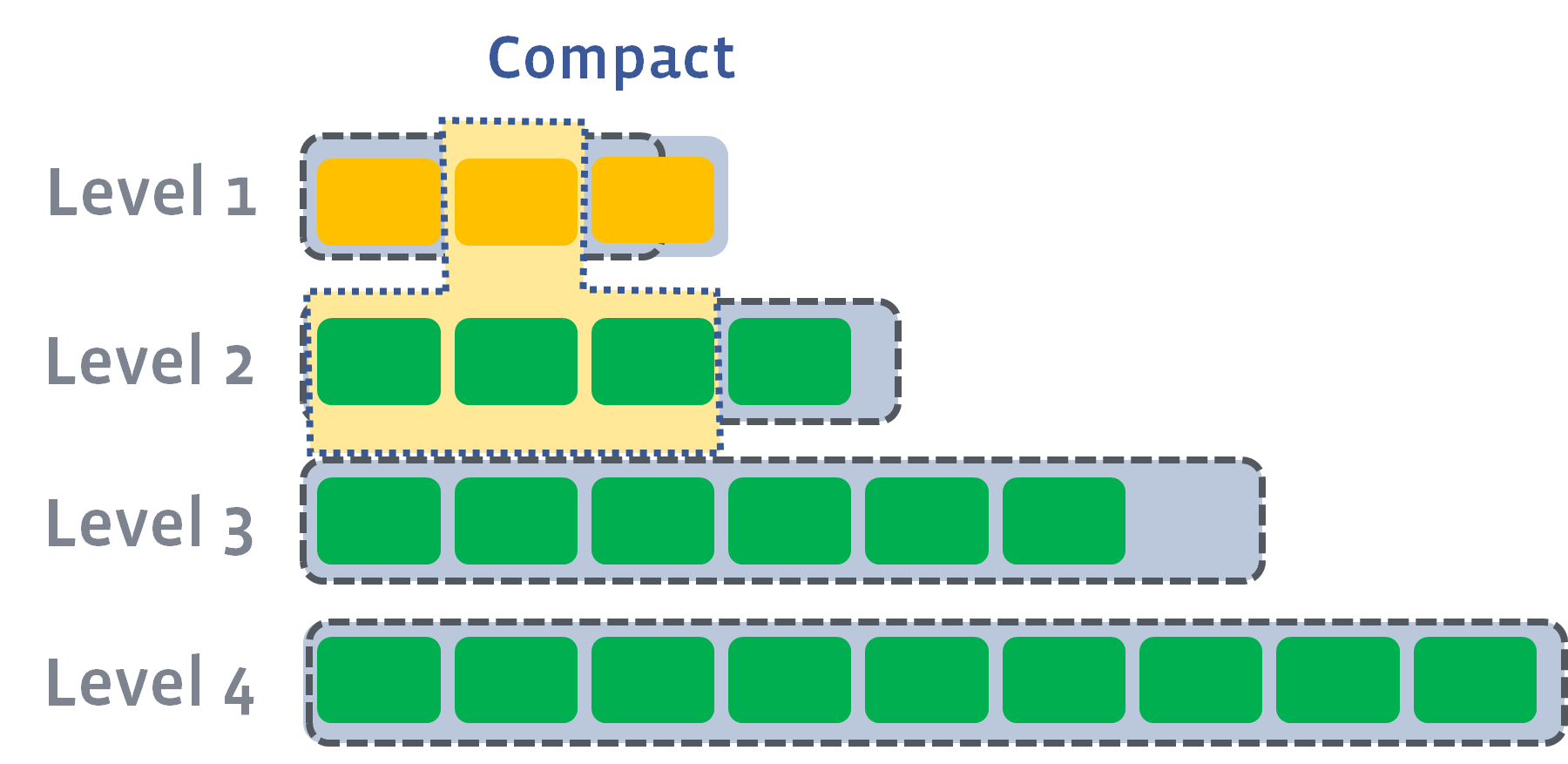
每个SSTable就好比一个有序数组/链表,多个SSTable的合并就是前文 链表双指针技巧汇总 中合并多个有序链表的逻辑。
这样,越靠上层的数据越新,越靠下层的数据越旧,且算法保证同一层的若干SSTable的key不存在重叠:
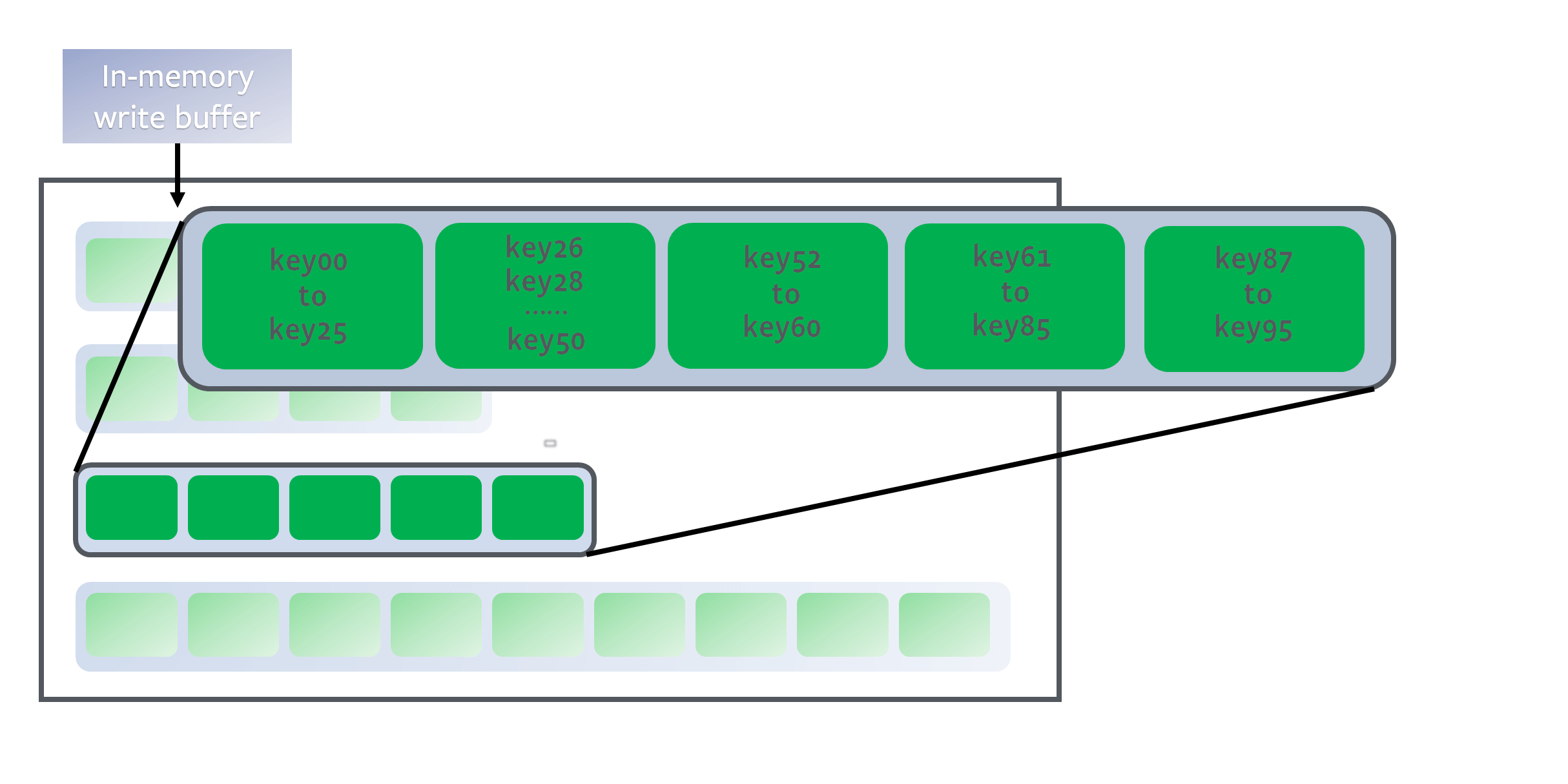
那么假设给一个目标键key27,我们只需要从上到下遍历层,并在每一层中使用 二分查找算法 找到键区间包含key27的SSTable,然后用布隆过滤器快速判断一下key27是否存在这个SSTable中。
如果存在,由于SSTable中的键也是有序的,可以再次运用 二分查找算法 找到键对应的值。
这样,借助 LSM 树的层级结构和SSTable的有序性,就能利用二分搜索提升查找效率,避免线性查找键值对。
以上就是本文的全部内容,如果你对 LSM 树的更多实现细节感兴趣,欢迎和我探讨。推荐一些学习资料:
LevelDB 的代码仓库:https://github.com/google/leveldb/issues
RocksDB 的 wiki:https://github.com/facebook/rocksdb/wiki
《数据库系统内幕》《精通 LevelDB》这两本书也不错。
标签:memtable,浅谈,存储系统,LSM,SSTable,key,磁盘,数据 From: https://www.cnblogs.com/labuladong/p/17023993.html更多高质量干货文章,请关注我的微信公众号:labuladong