DFS
深度优先搜索会搜得比较深,当搜到叶子结点的时候就会回溯
graph TD; a-->b-->d-->i-->r a-->c-->g-->n b-->e-->k b-->f-->m c-->h-->p d-->j e-->l g-->o h-->q i-->s该图的深搜序列就是:
a->b->d->i->r->i->s->i->d->j->d->b->e->k->e->l.....h->q
可以把深搜看成一个很执着的人,不管走哪条路,只有走到头才会回头,而且回头的时候也不是一下回到起点,而是一边回头一边看有没有新的路可以走
使用的数据结构是 stack,使用的空间和我们的高度成正比,不具有最短性
每个 dfs 都对应一个 搜索树
我们在拿到题目的时候,需要思考,我们用怎么样的顺序来遍历,才会最快捷
核心思想是:回溯,剪枝
每次存的都是路径,也不需要存整个搜索树,回溯的时候要注意恢复现场
模板
int dfs(int u)
{
st[u] = true; // st[u] 表示点u已经被遍历过
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j]) dfs(j);
}
}
例题
给定一个整数 n,将数字 1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤71≤n≤7
输入样例:
3输出样例:
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
第一层有 1,2,3
第二层比如 1 的子节点只有 2 和 3,因为不能重复
#include<iostream>
using namespace std;
const int N = 10;
int n;
int path[N];
bool st[N];
// u = 1,就是第一层,u = 2,就是第二层...
void dfs(int u)
{
if(u == n)
{
for(int i = 0;i < n;i++)
{
cout << path[i] << " ";
}
cout << endl;
return;
}
for(int i = 1;i <= n;i++)
{
if(!st[i])
{
path[u] = i;
st[i] = true;
dfs(u+1);
st[i] = false;
}
}
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n;
dfs(0);
return 0;
}
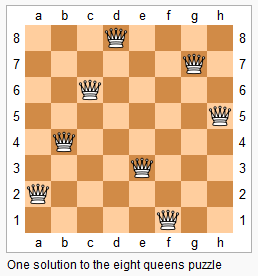
n−n−皇后问题是指将 nn 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中
.表示某一个位置的方格状态为空,Q表示某一个位置的方格上摆着皇后。每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4输出样例:
.Q.. ...Q Q... ..Q. ..Q. Q... ...Q .Q..
先看第一行皇后可以放哪一列,枚举每一行皇后放哪一行上去
搜索顺序和全排列是一样的
这题要注意剪枝,也就是不符合我们规则的序列,要及时停止
比如说我们已经有序列 1,3
这个时候我枚举了一个 4,也就是在 第 3 行,第 4 列枚举一个皇后,这个时候我去判断下是否和我已经有的皇后冲突,如果冲突,那么就直接 return,也就不用继续往下搜了
#include<iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool col[N],dg[N],udg[N];
// u = 1,就是第一层,u = 2,就是第二层...
void dfs(int u)
{
if(u == n)
{
for(int i = 0;i < n;i++)
{
puts(g[i]);
}
puts("");
return;
}
for(int i = 0;i < n;i++)
{
if(!col[i] && !dg[u+i] && !udg[n-u+i])
{
g[u][i] = 'Q';
col[i] = dg[u+i] = udg[n-u+i] = true;
dfs(u+1);
col[i] = dg[u+i] = udg[n-u+i] = false;
g[u][i] = '.';
}
}
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n;
for(int i = 0;i < n;i++)
{
for(int j = 0;j < n;j++)
{
g[i][j] = '.';
}
}
dfs(0);
return 0;
}
BFS
更像一个海王,她可以同时看很多条路
graph TD; a-->b-->d-->i-->r a-->c-->g-->n b-->e-->k b-->f-->m c-->h-->p d-->j e-->l g-->o h-->q i-->s比如这个树,第一次遍历会把 b 和 c 遍历到,第二层会把 b e f g h 全部遍历到才会到下一层
使用的数据结构是queue,使用的空间就是 2h,具有最短路性质
当每条边的权重一样的时候,我们搜到的一定是最短路
模板
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);
while (q.size())
{
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true; // 表示点j已经被遍历过
q.push(j);
}
}
}
例题
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m)处,至少需要移动多少次。
数据保证 (1,1)处和 (n,m)处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0输出样例:
8
首先我们将与起点距离为 1 的点放进来
graph TD 0,0-->1,0再把距离为 2 的点放进来
以此类推把距离为 3 的点放进来
graph TD 0,0-->1,0-->2,0-->3,0-->4,0-->4,1-->4,2 2,0-->2,1-->2,2-->2,3-->2,4-->1,4-->0,4 2,2-->1,2-->0,2-->0,3 2,4-->3,4-->4,4由于终点是第八层被扩展到的,所以起点到终点的距离是 8
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
typedef pair<int,int> PII;
int n,m;
int g[N][N];
int d[N][N];
PII q[N*N];
int bfs()
{
int hh = 0,tt = 0;
q[0] = {0,0};
memset(d,-1,sizeof d); //全部初始化为 -1
d[0][0] = 0;
int dx[4] = {-1,0,1,0},dy[4]={0,1,0,-1}; //用向量模拟上下左右
while(hh <= tt)
{
auto t = q[hh++];
//枚举四个方向
for(int i = 0;i < 4;i++)
{
int x = t.first + dx[i],y = t.second + dy[i];
//前四个是约束边界,g[x][y] = 0 代表是空地,d[x][y] = -1 代表没有走过
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1;
q[++tt] = {x,y};
}
}
}
return d[n-1][m-1];
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n >> m;
for(int i = 0;i < n;i++)
{
for(int j = 0;j < m;j++)
{
cin >> g[i][j];
}
}
cout << bfs() << endl;
return 0;
}
在一个 3×3 的网格中,1∼8 这 8 个数字和一个
x恰好不重不漏地分布在这 3×3 的网格中。例如:
1 2 3 x 4 6 7 5 8在游戏过程中,可以把
x与其上、下、左、右四个方向之一的数字交换(如果存在)。我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3 4 5 6 7 8 x例如,示例中图形就可以通过让
x先后与右、下、右三个方向的数字交换成功得到正确排列。交换过程如下:
1 2 3 1 2 3 1 2 3 1 2 3 x 4 6 4 x 6 4 5 6 4 5 6 7 5 8 7 5 8 7 x 8 7 8 x现在,给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
输入格式
输入占一行,将 3×3 的初始网格描绘出来。
例如,如果初始网格如下所示:
1 2 3 x 4 6 7 5 8则输入为:
1 2 3 x 4 6 7 5 8输出格式
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出 −1。
输入样例:
2 3 4 1 5 x 7 6 8输出样例
19
把所有状态,看成图论当中的一个点,如果某一个状态通过某种操作可以变成另一个状态的话,就连一条单向边,边的权重都是 1
那也就变成了 给定一个起点,求走到终点要多少步
那么如何表示一个点,也就是一个状态?
--直接用一个字符串表示一个状态,如“1234x5678”
如何把状态压入队列?
--queue
如何记录每一个状态的距离?
--unordered_map<string,int> dist
如何判断一个状态能变成哪些状态?
例如 “1234x5678”
我们先将其恢复成 3x3 的样子,然后枚举 x 的上下左右,再将枚举出来的矩阵恢复成字符串
#include<iostream>
#include<algorithm>
#include<queue>
#include<unordered_map>
using namespace std;
int bfs(string start)
{
string end = "12345678x";
queue<string> q;
unordered_map<string,int> dist;
q.push(start);
dist[start] = 0;
int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};
while(q.size()){
auto t = q.front();
q.pop();
int distance = dist[t];
if(t == end)
{
return distance;
}
// 状态转移部分
// 用k 来存 x 的位置,find(x) 会返回x的下标
int k = t.find("x");
int x = k/3, y = k%3; // 把一维数组下标转化成二维数组下标
for(int i = 0;i < 4;i++)
{
int a = x+dx[i];
int b = y+dy[i];
if(a >=0 && a < 3 && b >= 0 && b < 3)
{
swap(t[k],t[a*3+b]);
if(!dist.count(t))
{
//没有找到过的状态,更新下距离
dist[t] = distance+1;
q.push(t);
}
// 恢复状态
swap(t[k],t[a*3+b]);
}
}
}
return -1;
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
string start; //state 来存初始状态
for(int i = 0;i < 9;i++)
{
char c;
cin >> c;
start += c;
}
cout << bfs(start) << endl;
return 0;
}