首页 > 其他分享 >浅谈线段树

浅谈线段树

时间：2022-12-24 19:57:53浏览次数：63  
标签：浅谈 dep 线段 tree mid 端点 区间

本篇将会记录我的线段树学习时长

其实很早就想学了，但由于奇妙的原因咕了好久

2021.1.5

今天讲讲线段树概念和初始建树

线段树的概念

线段树是个二叉树

线段树的每个区间是输入数据的数组下标，即 \([1,3]\) 是表示 \(a_1\) 到 \(a_3\) 中的数

它的根节点就是整个区间的数

它的叶子节点的区间只有 \(1\) 个数

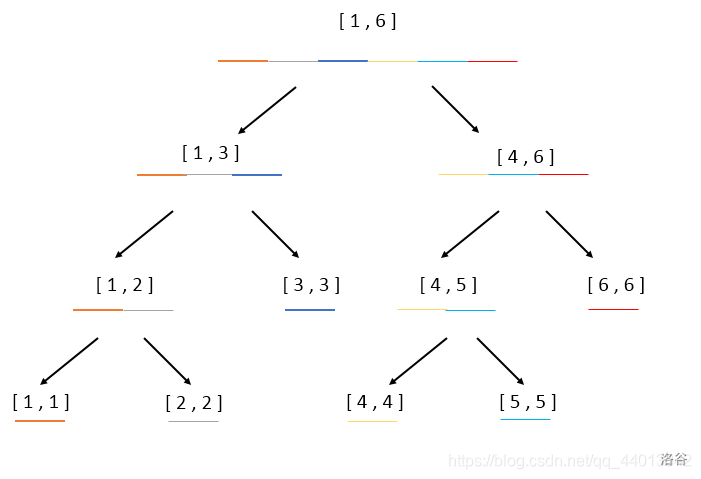
如图即为一棵线段树

我偷了一棵给你们欣赏

线段树的建树

作为一棵树，那么肯定是要先建树啦（废话）

给个场景吧

现在给你 \(n\) 个数，\(a_1\)，\(a_2\)，…… \(a_n\)，要求你建一棵线段树

题目简介草率，凑合着看

我们先用结构体定义一个线段树

struct SegmentTree{
	int l, r, sum;//每层的左端点和右端点，当前层数的和 
} tree[N << 2 | 1];

相信结构体内的内容都能看明白

然后在输入后，我们开始建树

\(dep\) 表示当前遍历到的层数，默认根节点为 \(1\)

\(l\)，\(r\) 表示左右端点的下标

\(As\) \(we\) \(know\)，由于线段树是个二叉树，所以他的左儿子即为 \(dep << 1\)，右儿子即为 \(dep << 1 | 1\)

\(Then\)，我们看看上面我偷来的那颗线段树，发现，他的左子树的区间即为 \([l, (l + r) >> 1]\)，右子树的区间即为\([((l + r) >> 1) + 1, r]\)

那我们递归建树即可

那么接下来如果到了叶子节点怎么办呢？

那就开始回溯

先将当前这层赋值与 \(tree[dep].sum\)（其实只有 \(1\) 个值了），然后回溯合并即可

下面贴上代码

#include <iostream>
#include <cstdio>

const int N = 1e5 + 7;

using namespace std;

struct SegmentTree{
	int l, r, sum;//每层的左端点和右端点，当前层数的和 
} tree[N << 2 | 1];

int a[N], n;

inline int read() {
	int n = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9') {
		if (c == '-')
			f = -f;
		c = getchar();
	}
	while (c >= '0' && c <= '9') {
		n = (n << 3) + (n << 1) + (c ^ '0');
		c = getchar();
	}
	return n * f;
}

void build(int dep, int l, int r) {//dep表示深度，从1开始。l表示左端点，r表示右端点 
	tree[dep].l = l, tree[dep].r = r;
	if (l == r) {
		tree[dep].sum = a[l];
		return ;
	} 
	int mid = (l + r) >> 1;
	build(dep << 1, l, mid);
	build(dep << 1 | 1, mid + 1, r);
	tree[dep].sum = tree[dep << 1].sum + tree[dep << 1 | 1].sum;//当前这个区间的和，就是他的左儿子的和+右儿子的和
} 

int main() {
	n = read();
	for (int i = 1; i <= n; i ++)
		a[i] = read();
	build(1, 1, n);
	return 0;
}

今天讲解完毕，我要去背诵政治了

2021.1.6

今天我们学学区间查询

为什么不讲单点查询和单点修改，因为其实你懂了区间查询，单点查询和单点修改就会了

区间查询：

进入正题

其实感觉并不难啊

给个背景，就是叫你求区间 \([x, y]\) 的和

题目简介草率，凑合着看

可以选择遍历整颗线段树，我们先用 \(dep\) 表示当前遍历到的深度（默认根节点为 \(1\)），\(x\)，\(y\) 表示当前求的区间，用 \(res\) 记录答案

操作步骤：

那么我们可以知道有 \(3\) 种状况

\(1.\) 如果区间 \([x, y]\) 包围了区间 \([tree[dep].l, tree[dep].r]\)

直接返回此区间的和即可

\(2.\) 如果要求区间的左端点把这个区间的左端点包围了

那么得继续往下搜，遍历左儿子，因为必须得让 \(tree[dep].r\) 更小，下次 \(mid\) 才会更小

\(3.\) 如果要求区间的右端点把这个区间的右端点给包围了

那么得继续往下搜，遍历右儿子，因为必须得让\(mid\)更大，就得让 \(tree[dep].l\) 变大

下面贴上代码

这份是将区间 \([tree[dep].l, tree[dep].r]\) 分成 \([tree[dep].l, mid]\) 和 \([mid + 1, tree[dep].r]\)

#include <iostream>
#include <cstdio>

const int N = 1e5 + 7;

using namespace std;

struct SegmentTree{
	int l, r, sum;//每层的左端点和右端点，当前层数的和 
} tree[N << 2 | 1];

int a[N], n, op, m;

inline int read() {
	int n = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9') {
		if (c == '-')
			f = -f;
		c = getchar();
	}
	while (c >= '0' && c <= '9') {
		n = (n << 3) + (n << 1) + (c ^ '0');
		c = getchar();
	}
	return n * f;
}

void build(int dep, int l, int r) {//dep表示深度，从1开始。l表示左端点，r表示右端点 
	tree[dep].l = l, tree[dep].r = r;
	if (l == r) {
		tree[dep].sum = a[l];
		return ;
	} 
	int mid = (l + r) >> 1;
	build(dep << 1, l, mid);
	build(dep << 1 | 1, mid + 1, r);
	tree[dep].sum = tree[dep << 1].sum + tree[dep << 1 | 1].sum;
} 

int query(int dep, int x, int y) {//dep表示深度，从1开始。l表示左端点，r表示右端点，x表示要求区间的左端点，y表示右端点 
	int res = 0;//返回的和 
	if (x <= tree[dep].l && y >= tree[dep].r)
		return tree[dep].sum;//如果区间[x, y]保包围了区间[l, r]，直接返回此区间的和即可 
    int mid = (tree[dep].l + tree[dep].r) >> 1;
	if (x <= mid)//如果要求区间的左端点把这个区间的左端点包围了 
		res += query(dep << 1, x, y);//继续往下搜，遍历左儿子，因为必须得让r更小，下次mid才会更小 
	if (y > mid)//如果要求区间的右端点把这个区间的右端点给包围了 
		res += query(dep << 1 | 1, x, y);//继续往下搜，遍历右儿子，因为必须得让mid更大，就得让l变大 
	return res; //返回答案 
}

int main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i ++)
		a[i] = read();
	build(1, 1, n);
	for (int i = 1, x, y, v; i <= m; i ++) {
		op = read();
		if (op == 2) {//区间查询 
			x = read(), y = read();
			cout << query(1, x, y) << endl;
		} else {//区间修改 
			x = read(), y = read(), v = read();
			continue;
			//暂未开发 
		}
	} 
	return 0;
}

这份是将区间 \([tree[dep].l, tree[dep].r]\) 分成 \([tree[dep].l, mid]\) 和 \([mid + 1, tree[dep].r]\)

#include <iostream>
#include <cstdio>

const int N = 1e5 + 7;

using namespace std;

struct SegmentTree{
	int l, r, sum;//每层的左端点和右端点，当前层数的和 
} tree[N << 2 | 1];

int a[N], n, op, m;

inline int read() {
	int n = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9') {
		if (c == '-')
			f = -f;
		c = getchar();
	}
	while (c >= '0' && c <= '9') {
		n = (n << 3) + (n << 1) + (c ^ '0');
		c = getchar();
	}
	return n * f;
}

void build(int dep, int l, int r) {//dep表示深度，从1开始。l表示左端点，r表示右端点 
	tree[dep].l = l, tree[dep].r = r;
	if (l == r) {
		tree[dep].sum = a[l];
		return ;
	} 
	int mid = (l + r + 1) >> 1;
	build(dep << 1, l, mid - 1);
	build(dep << 1 | 1, mid, r);
	tree[dep].sum = tree[dep << 1].sum + tree[dep << 1 | 1].sum;
} 

int query(int dep, int x, int y) {//dep表示深度，从1开始。l表示左端点，r表示右端点，x表示要求区间的左端点，y表示右端点 
	int res = 0;
	if (x <= tree[dep].l && tree[dep].r <= y)
		return tree[dep].sum;
    int mid = (tree[dep].l + tree[dep].r) >> 1;
	if (x < mid)
		res += query(dep << 1, x, y);
	if (y >= mid)
		res += query(dep << 1 | 1, x, y);
	return res; 
}

int main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i ++)
		a[i] = read();
	build(1, 1, n);
	for (int i = 1, x, y, v; i <= m; i ++) {
		op = read();
		if (op == 2) {
			x = read(), y = read();
			cout << query(1, x, y) << endl;
		} else {
			x = read(), y = read(), v = read();
			continue;
			//暂未开发 
		}
	} 
	return 0;
}

接下来将会是整个线段树最艰难（目前来说）的部分，区间修改

我可能不会一天更一会了，去肝 \(whk\) 了

2021.1.9

啊啊啊我学会了

别问我为什么咕了这么久

进入正题

还是先给个题面

给定 \(N\) 个数，\(a_1\)，\(a_2\)，\(a_3\)，，……，\(a_n\)，要求区间 \([x, y]\) 中的所有数加上 \(num\)

题目简介草率，凑合着看

最朴素的思想是我们可以选择暴力枚举 \([x, y]\) 中的数，那么最坏操作就是O(n)，超时先不说，这也没有用到线段树吧

那么我们引入一个懒标记的思想

懒标记就是将标记下传

分三种情况

\(1.\) 如果区间 \([x, y]\) 将区间 \([tree[dep].l, tree[dep].r]\) 包围了

那么我们就不需要下传，将这个区间直接更改即可，然后回溯

\(2.\) 如果要求区间的左端点把这个区间的左端点包围了

那么我们应该递归左子树，为什么给我去看区间查询

3.如果要求区间的右端点把这个区间的右端点给包围了

那么我们我们应该递归右子树，为什么同上

现在的关键是怎么下传（也就是如何正确打开懒标记）

下传的范围先确定是 \([l, mid]\)

然后这个的区间和改变，改变的数目即为数值 * （该区间）元素个数

然后将这个标记下传即为

tree[dep].lazy += v;

即将这一层记为 \(v\) 这个标记

在遍历完也要讲下传的一层的父节点置 \(0\)

现在我们再看看那颗我偷来的线段树

我们假设这 \(6\) 个元素分别是 \(1\)，\(2\)，\(3\)，\(4\)，\(5\)，\(6\)

那我们看一下如果在区间 \([2, 4]\) 中加上 \(5\) 的过程

mid = 3
tree[dep].lazy = 0
tree[dep].sum = 6(原先的)
dep = dep << 1 (x <= mid,y > mid)

这个时候x == tree[dep].l, y > tree[dep].r调用add
tree[dep].lazy = 5
tree[dep].sum = 21(原来的)
dep >> = 1(回到上一层)
mid = 3
dep = dep << 1 | 1(x <= mid(用过了))，(y > mid)

mid = 5
tree[dep].lazy = 0
tree[dep].sum = 15(原来的)
dep << 1(x <= mid)

mid = 4
tree[dep].lazy = 0
tree[dep].sum = 9
dep << 1(x <= mid)
  
然后这时候发现x <= tree[dep].l, y >= tree[dep].r, 调用add
tree[dep].lazy = 5
tree[dep].sum = 9(5 + 4)
接下来返回

于是就成功插入
  
合并过程就不用说了，自行思考

接下来贴出代码

#include <iostream>
#include <cstdio>

const int N = 1e5 + 7;

using namespace std;

struct SegmentTree{
	int l, r, sum;//每层的左端点和右端点，当前层数的和 
	int lazy;//懒标记，待活详细讲 
} tree[N << 2 | 1];

int a[N], n, op, m;

inline int read() {
	int n = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9') {
		if (c == '-')
			f = -f;
		c = getchar();
	}
	while (c >= '0' && c <= '9') {
		n = (n << 3) + (n << 1) + (c ^ '0');
		c = getchar();
	}
	return n * f;
}

void build(int dep, int l, int r) {//dep表示深度，从1开始。l表示左端点，r表示右端点 
	tree[dep].l = l, tree[dep].r = r;
	if (l == r) {
		tree[dep].sum = a[l];
		return ;
	} 
	int mid = (l + r) >> 1;
	build(dep << 1, l, mid);
	build(dep << 1 | 1, mid + 1, r);
	tree[dep].sum = tree[dep << 1].sum + tree[dep << 1 | 1].sum;
} //建树 

inline void add(int dep, int l, int r, int v) {
	tree[dep].lazy += v;//将标记传于dep这个深度 
	tree[dep].sum += v * (r - l + 1);//区间和改变，改变的值即为原来 + 元素个数 * 改变的值 
}//更改 

inline void pushdown(int dep, int l, int r) {
	if (! tree[dep].lazy)
		return ;//如果这个数值为0，下放就毫无意义
	int mid = (l + r) >> 1;
	add(dep << 1, l, mid, tree[dep].lazy);
	add(dep << 1 | 1, mid + 1, r, tree[dep].lazy);//下传标记 
	tree[dep].lazy = 0;//该节点清零 
	return ; 
} //下传 

int query(int dep, int x, int y) {//dep表示深度，从1开始。l表示左端点，r表示右端点，x表示要求区间的左端点，y表示右端点 
	int res = 0;//返回的和 
	if (x <= tree[dep].l && y >= tree[dep].r)
		return tree[dep].sum;//如果区间[x, y]保包围了区间[l, r]，直接返回此区间的和即可 
    int mid = (tree[dep].l + tree[dep].r) >> 1;
	pushdown(dep, tree[dep].l, tree[dep].r); 
	if (x <= mid)//如果要求区间的左端点把这个区间的左端点包围了 
		res += query(dep << 1, x, y);//继续往下搜，遍历左儿子，因为必须得让r更小，下次mid才会更小 
	if (y > mid)//如果要求区间的右端点把这个区间的右端点给包围了 
		res += query(dep << 1 | 1, x, y);//继续往下搜，遍历右儿子，因为必须得让mid更大，就得让l变大 
	return res; //返回答案 
}//区间查询 

void update(int dep, int x, int y, int v) {
	if (x <= tree[dep].l && y >= tree[dep].r) {//如果区间[x, y]保包围了区间[l, r]，直接将这层标记即可，不用下传 
		add(dep, tree[dep].l, tree[dep].r, v);//看，dep没有变化，因为只需传送这层即可 
		return ;
	}
    int mid = (tree[dep].l + tree[dep].r) >> 1;
	pushdown(dep, tree[dep].l, tree[dep].r);//每次递归前标记下传 
	if (x <= mid)
		update(dep << 1, x, y, v);
	if (y > mid)
		update(dep << 1 | 1, x, y, v); 
	tree[dep].sum = tree[dep << 1].sum + tree[dep << 1 | 1].sum;
}//区间修改 

int main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i ++)
		a[i] = read();
	build(1, 1, n);
	for (int i = 1, x, y, v; i <= m; i ++) {
		op = read();
		if (op == 2) {//区间查询 
			x = read(), y = read();
			cout << query(1, x, y) << endl;
		} else {//区间修改 
			x = read(), y = read(), v = read();
			update(1, x, y, v);
		}
	} 
	return 0;
}

其实细心的人发现了，只要把 \(int\) 改成 \(longlong\) 就能过掉P3372线段树1了（/hj）

老菜逼讲的线段树到此结束，谢谢观看

标签：浅谈,dep,线段,tree,mid,端点,区间
From： https://www.cnblogs.com/Kalium/p/17003281.html

相关文章

  • 浅谈电动汽车充电桩建设现状及规划方案
    0引言  随着能源转型步伐的加快，我国经济由高速发展迈向高质量发展。“十三五”以来，全省将节能、削煤、降碳与调结构、治污染、惠民生相结合，实施能耗总量与强度双重控制[1......
  • 浅谈地址，section，vstart
    地址：地址只是数字，描述各种符号在源程序中的位置，它是源代码文件中各符号偏移文件开头的距离。由于指令和变量所占内存大小不同，故他们的偏移量参差不齐。由编译器给各符号编......
  • 浅谈商城项目
         很多同学会说，现在很多培训机构都在做电商这个项目，那我们做这个项目的意义又是什么呢？    1、作为学生而言，刚学完SSM框架，很多基础掌握不牢靠，因此针对初学者而言......
  • 线段树复习笔记——可持久化线段树（主席树）
    可持久化线段树——主席树引入（P3834【模板】可持久化线段树2-洛谷）看看题面：题目描述如题，给定\(n\)个整数构成的序列\(a\)，将对于指定的闭区间\([l,r]\)查询其......
  • HDU4553 线段树维护最长连续区间
    //题意：（略了）//思路：这里很明显是要维护区间最大连续子段，按照以下优先级查找//A1.左边区间的连续子段是否满足//A2.左右两个区间中间合并起来的子段是否满足......
  • 反射和对象序列化浅谈
    反射c++本身是没有反射机制的。反射是什么？我认为是运行时对象信息库，反射就是在需要获取对象信息的时候使用，在做类型转换的时候使用，获取对象实例的时候使用...统一一下就是......
  • P3372 【模板】线段树 1
    P3372【模板】线段树1题目简述对于一段数列，有如下两种操作1xyk：将区间\([x,y]\)内每个数加上\(k\)。2xy：输出区间\([x,y]\)内每个数的和。思路线段树......
  • 线段树复习笔记——综合应用（吉司机线段树）
    线段树的综合应用接下来，以洛谷P6242【模板】线段树3（超级毒瘤）为例，来看一下线段树的综合应用。先来看一下此题题意，很熟悉的题面：题目描述给出一个长度为\(n\)的数列......
  • 浅谈Keil-MDK创建项目&编译过程---Code-data,RO-data,RW-data,ZI-data
    浅谈Keil-MDK创建项目&编译过程---Code-data,RO-data,RW-data,ZI-data​​一、编译过程​​​​二、MDK编译工具​​​​(1）创建一个新的工程​​​​(2）添加startup（启动文......
  • 795前缀和，线段树，树状数组
    题目描述输入一个长度为\(n\)的整数序列。接下来再输入\(m\)个询问，每个询问输入一对\(l,r\)。对于每个询问，输出原序列中从第\(l\)个数到第\(r\)个数的和。输......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99