1. CF 场计划
计划内容
根据能力情况完成 div1 的 ABCD 或 div2 的 CDEF(暂定),难度 \(\le 2500\) 的。
计划目标
半年内完成 \(10\) 场 CF 的参与,以及 \(20\) 场 CF 的总结和题解。
计划进度
当前比赛参与场数:\(1\)
当前比赛完结场数:\(1\)
列表:
2. CF 思维/代码训练计划
计划内容
设当前 \(\text{rat} = 1900, \text{pts}=0\)。
- 随机选择或有 tag 选择一道难度为 \(\text{rat}\) 的题目。
- \(35 \min\) 内完成,\(\text{pts}+1 \to \text{pts}\) ;
否则 \(\text{pts}-1 \to \text{pts}\) ; - 若 \(\text{pts}=-4\),\(\text{rat}-100 \to \text{rat}\); \(\text{pts}=4\),\(\text{rat}+100 \to \text{rat}\)。
- 返回步骤 \(1\)。
计划目标
完成 \(150\) 题;打到 \(\text{rat}=2300\)。
计划进度
当前 \(\text{rat}=1900\),题数 \(0\)。
列表:
1.
3. AT 选做计划
比较随意,乱做。
计划进度
题目数: \(0\)。
4. 补算法计划
主要寒假完成:
- 计数(重要)
- dp
- 字符串
- 图论(重要)
- 数据结构
- 数论
计划进度
暂无。
5. Trick 积累计划
有想法就发布在博客园,越多越好。
6. 完成题目列表
| Date | ProID | Diff | Tag1 | Tag2 | Tag3 | 描述 -- Description | 题目解答及技巧 -- Solution |
|---|---|---|---|---|---|---|---|
| 12.4 | CF1736D | *2200 | 思维 | 构造 | 给定一个长度为 \(2n\) 的 01 序列 \(S\)。可以选择一个下标的子序列,然后每个下标向右移位。仅能进行一次操作,构造一个方案,使得 01 序列可以划分成两个相等的子序列。 | 这道题通过发现合法的性质实在是不好做。但是我们有别的思路:构造一种方案,使得划分的方案十分简单。怎么划分简单呢?利用长度为 \(2n\) 的性质,两位两位考虑,一位给序列 A,另一个给序列 B。这样做法浮出水面:调整使得 \(S_{2n-1}=S_{2n}\),容易做了。 | |
| 12.4 | CF1296F | *2100 | 代码 | 构造 | 贪心 | 给定一棵 \(n\) 个点的树的结构,构造一组边权。满足 \(m\) 个条件,每个条件可以写成 \((u,v,w)\) 的形式,表示从 \(u\) 到 \(v\) 的边权最小值为 \(w\)。\(n,m \le 5000\) | 这题刚到手的时候立马就有了思路。按顺序处理这些限制。初始每条边赋 \(\infty\)。在不破坏先前的限制的情况下,任意选择一条边选上,赋上这个边权,找不到无解。实现的时候我有几个问题。第一,处理限制的顺序。本来想的是按照限制路径长度排序,但实际上路径不仅仅有包含关系,错误。边权从大到小显得合理又简单。第二,关于同边权时候的处理。如果一条边还没有用上,并且被先前的限制所约束。但先前的和当前的限制值相同,那么这条边还是能用上的。尽管是 *2100,也耗费了 40min 解决,代码量较大。 |
| 12.4 | CF1283F | *2200 | 思维 | 构造 | 图论 | 一棵树,编号为 $ i $ 的点权值为 $ 2^i $,规定一条边的权值为,这条边连接的两个点中深度较大的点的子树的点权之和 。题目给出总点数 $ n $ 并按照边权由大到小,给出每条边的深度较浅的点的编号。构造原树,输出根以及连边情况。 | 这题其实最开始看错了,导致完全没有思路(看错的地方加粗了)。我们不难发现给出的第一个点一定是根节点。从大到小考虑边权不太行的通,如果倒着看会好看一些。没有"上榜"的节点都是叶子节点,这很显然。然后倒数的几个,子树肯定很小,但是实际上也说不好。可以肯定的是,上榜的倒数第一肯定只有一个子节点——叶子结点中编号最小者(易反证)。把这条边连上,再去看倒数第二……如果当前连的上榜的节点已经找到了所有儿子,那么又可以把它看做叶子节点了……以此类推,似乎这样可以根据拓扑的思路建出原图。这题必须得把关键代码放出来讲述。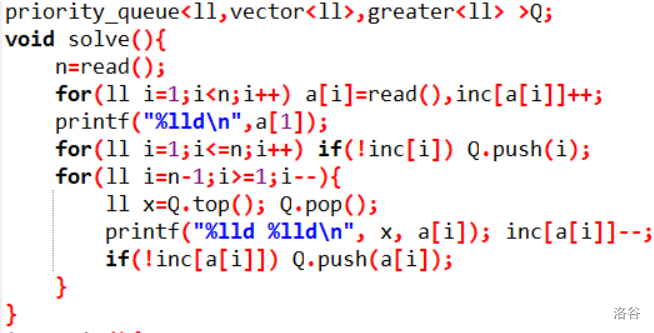 |
| 12.4 | CF1096E | *2500 | 思维 | 计数 | GT | 小明在打比赛,包括小明自己一共有 \(p\) 名选手参赛,每个人的得分是一个非负整数。最后的冠军是得分最高的人,如果得分最高的人有多个,就等概率从这些人中选一个当冠军。现在小明已知了自己的得分大于等于 \(r\),所有选手的得分和为 \(s\)。求小明获胜的概率,结果对 \(998244353\) 取模。\(s,r \leq 5000,p \leq 100\) | 自己做出了 *2500 的计数 qwq首先暴力的推式子,枚举最高分和最高分人数不必多说,也十分好推;但是推到最后会发现需要计算一个函数 \(f(a,b,c)\) 表示 \(b\) 个数,每个数为整数在 \([0,c]\) 的范围内,总和为 \(a\) 的方案数。这个数字大家推的容斥比较多,我用生成函数推了一下:\(f(a,b,c) = ((\sum \limits_{k=0}^c x^k)^b) [x^a]\)这个的展开很基础,分子可以二项式定理暴展,分母有现成的柿子。所以这个问题被 \(O(b)\) 解决了。那么仔细算一下实际的复杂度,可以通过。由于太晚,脑抽没计算上选取一些人与小明同分的方案,调了挺久。 |
| 12.5 | CF1154F | 2100 | 诈骗 | dp | 商店里有 \(n\) 双鞋,每双鞋都有价格。要买其中的 \(k\) 双。有 \(m\) 种套餐,第 \(i\) 种套餐代表如果一次购买 \(x_i\) 双鞋则其中最便宜的 \(y_i\) 双免费。这 \(m\) 种套餐每种都可以用任意次。现在请求出买严格 \(k\) 双鞋的最小化费。\(1~\leq~n,~m\leq~2~\times~10^5\)\(1~\leq~k~\leq~\min(n, 2000)\) | 没啥好说的。注意到一定会选择最小的 \(k\) 个物品,每次选取一定是选择区间更优。\(O(k^2)\) dp 即可。 | |
| 12.5 | CF1265E | *2100 | 思维 | 计数 | 期望 | Bot 打的游戏有 \(n\) 关,每关有一定概率过关,如果没过回到第一关。求期望通关次数。 | 一道很好的期望题,提供两种思路。1. 正推法:从左到右考虑。这里我们用到期望的与自己列关系式。如果当前成功,期望值是 \(f(x-1) +1\),否则是 \(f(x-1)+1+f(x)\),结合概率解出来递推式;2. 倒推法:考虑当前镜子问到最后的镜子的期望(考虑后面),列出来和 \(f(1)\) 有关。这里我们用到 通过未知数列出方程,求解未知数,能把 \(f(1)\) 解出来。最后再推一遍。 |
| 12.6 | CF1618G | *2200 | 代码 | 图论 | 图的联通性 | 在交易系统中,你可以用一个价值为 \(x\) 的物品换取一个价值不超过 \(x+k\) 的物品(\(k\) 为常数)。给定你手中的 \(n\) 个物品,以及系统的 \(m\) 个物品分别的价值,有 \(q\) 次询问,对于每次询问,给定 \(k\),求经过若干次交易后你手上物品的总价值最大是多少。注:询问之间互相独立。\(1\le n,m,q\le2\times 10^5\) | 首先,按到这题要首先想到图论:考虑一定会取能换到的最大的 \(n\) 个物品。如果能关于 \(k\) 建立一个图,用并查集 or 启发式合并很容易做。但是 \(k\) 会动,考虑离线,从小到大考虑 \(k\),每次动态加边即可。具体实现的时候可以按照价值排序,每次合并两个区间,这样求新的价值时可以利用前缀和,好搞一些(所以这题 tag 给的代码) |
| 12.6 | CF1553F | *2300 | 代码 | 数据结构 | 递推维护 | 给定一个由不同数组成的序列 \(a\),定义 \(p_k\) 为:\(p_k = \sum_{i=1}^k \sum_{j=1}^k a_i \bmod a_j\) 其中 \(a_i \bmod a_j\) 表示 \(a_i\) 除以 \(a_j\) 的余数。对于每个 \(i \in [1,n]\),求出 \(p_i\)。 | 考虑到 \(p_i = p_{i-1} + \sum \limits_{k=1}^{i-1} a_i \bmod a_k + \sum \limits_{k=1}^{i-1} a_k \bmod a_i\) 是这题的关键。我们致力于找到两只 log 的做法。 第一部分:是比较难的地方。考虑拆掉 \(\bmod\) 之后要求的 \(\sum \left\lfloor\dfrac{a_i}{p}\right\rfloor p\),前面的一个数会 \(p\) 给 \(a_i\) 的贡献怎么统计?维护 BIT,给所有 \(p\) 的倍数加上 \(p\) ,可以发现维护的 BIT 的前 \(a_i\) 项和就是我们要的(巧妙之处)第二部分:比较好想,直接枚举 \(a_i\) 的倍数,大力统计。\(\bmod\) 也要拆开。由于数不重复,易知枚举倍数没必要超过 \(3\times 10^5\),复杂度是对的。 |
| 12.6 | CF863F | *2200 | 综合 | mcmf | 差分建图 | 现有一个长度为 \(n\) 的未知数组\(A\) , 每个元素都是 \([c_i,d_i]\) 内的整数。\(c,d\) 为给定数组。设 \(cnt(i)\) 为 \(i\) 在 \(A\) 中的出现次数。求出在所有满足条件的数组中,式子的最小值 :\(\sum\limits_{i=1}^ncnt(i)^2\) | 数据范围小,费用流;看到平方,考虑差分;第一次流入费用为 \(1\),第二次为 \(3\),……,这样其实可以把同一种数给拆成很多点。流入的时候每个点都只能流一次,费用如上述所示依次排列。算法一定会选择一个前缀去流,也就是对应的平方。 |
| 12.10 | ABC272G | *2187 | 思维 | rand | 绝对众数 | 给出一个长度为 \(N\) 的序列 \(A\), 其中 \(A\) 的每个元素均为正整数且互不相同。你需要选择一个的正整数 \(M\),并执行一次下列操作: 对于 \(1\leq i\leq N\),将 \(A_i\) 替换为 \(A_i\) \(\mod M\) 。 找到一个数 \(M\) 使得序列 \(A\) 中存在次数超过一半的绝对众数,或报告误解。 \(N \le 5000\),其他 \(\le 10^9\) |
这真的是一个很牛逼的随机化题目。我们发现众数很多,那么在某种正确情况下,随机选择两个数,随机到两个包含在众数中的概率极大(\(\dfrac{1}{4}\)),每次选中两个数,枚举其差的因数去暴力判断,多做几十次就可以了。 如果遇到这种被选中概率很高,枚举困难、判断困难,可以考虑随机化。 |
| 12.17 | CF1767E | 代码 | NPC | 折半状压 | 简化题意:一般图带权最大独立集的 \(n=40\) 的解。 | 这是一个很经典、很重要的套路:拆位。分成前 \(20\) 位和后 \(20\) 位处理,然后合并。具体实现,可以对于前 \(20\) 位预处理(暴搜或状压)出一个表,可以查询任意子集的最大独立集,后 \(20\) 位先预处理,然后在前 \(20\) 位抠掉不能取的,去查表。复杂度 \(O(2^mm^2)\) 可以通过。 |