cs231n笔记
动量
原始的SGD优化方法是
\[x_{t+1}=x_t-\alpha\nabla f(x_t) \]就是单纯在梯度方向下降,加入动量的目的是为了加速学习,也就是加快梯度下降的速度
如何做到加快梯度下降的速度,模仿滚石,滚石在梯度方向上肯定是越滚越快,但如果有拐弯的话也会减速,因为每个时刻的移动,不仅仅是本时刻的梯度,还有之前积累的速度在影响,动量就是法就是把过去时刻积累的速度也考虑到本次更新之中。
带有动量的SGD本质:使用指数加权平均之后的梯度代替原梯度进行参数更新。因为每个指数加权平均后的梯度含有之前梯度的信息,动量梯度下降法因此得名。
\[v_{t+1}=\rho v_t +\nabla f(x_t) \]\[x_{t+1}=x_t-\alpha v_{t+1} \]反向传播
反向传播做的事情其实就是求loss对于某个参数的偏导数,直接求解析解过于复杂,使用链式法则配合计算图,把偏导数转化为计算图中每个节点的值,最后相乘,就可以很容易求得loss对于某个参数的偏导数
计算方法
如下图,绿色的值是前向传播时计算出来的值,计算图中每个节点都有一个对应的值,红色的值是从后面反向传播到这个节点的梯度值,反向传播只求与当下计算图节点有关的表达式的梯度,这里的节点是乘法,我们要求w0和x0的梯度,求法如下
- 写出计算图的表达式\(f=w_0 * x_0\)
- \(\frac {df}{dw_0}=local\ gradient*upstream\ gradient=x_0(直接求导)*0.2(上游梯度)=-0.2\)

最后如何获得loss关于某个参数的梯度
例如这里,loss关于w2的梯度
只需要从最后开始,向前回溯,一路上的红色数字相乘就是loss关于w2的梯度

值得一提的是max gate
这里只有z和w中的较大者会获得上游的梯度,而且是直接继承,较小者的梯度直接为零
事实上这个也很好理解,因为只有较大者会进行前向传播,也就是会对loss产生影响,较小者则不会

前向传播中的多分支
如果一个节点在前向传播时拥有多分支,那么反向传播时的上游梯度就是多个分支的梯度之和

卷积的计算
基本计算方法
对应元素相乘再相加,再加上bias
如下图,input是一个5*5矩阵,卷积核是3*3矩阵,bias是1
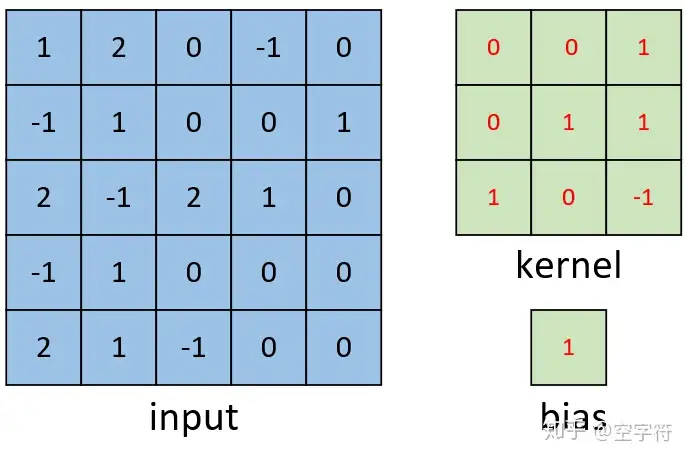
计算方法就是\(1*0+2*0+0*0+-1*0\cdots +bias=2\)
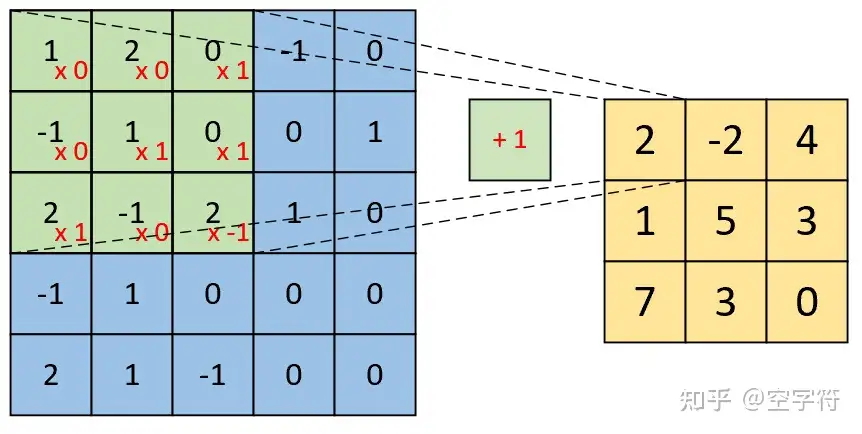
下一个元素就是把卷积核向右移动一位,在重复操作
如果stride=2,那就是移动两位,但不是所有的stride都可行,如果是3的话,就会超过边界
填充
有时为了获得我们想要的output大小,我们需要针对input进行填充(padding),填充的方法很简单,就是在周围一圈补上0

卷积输出计算公式
结合padding我们的output计算公式可以总结为
\[outputsize=(inputsize + 2*padding -kernel\_size)/stride+1 \]这个公式不用死记,下面我用非常便于理解的方法描述这个推导。卷积就是对相邻的一片数据进行加权求和得到一个数的一种“合并”操作,将此操作对输入张量进行滑动扫描以得到输出张量。循着这个过程,我们很容易推导出卷积输出尺寸的计算公式。
(1)注意padding指的是两边同时补零,所以补零后输入尺寸相当于变成了i+2p;
(2)用卷积核扫描的时候,想象一把尺子在桌子上从左移动到右,受到左右边框的界限,它的移动范围只有i+2p-k大小。
(3)如果每次移动的步长是s,实际上移动的步数就是 (i+2p-k)/s,但移动的步数必须是整数,因为不能出界,如果最后一步哪怕还差一点也不能算,所以必须要向下取整。
(4)即使一步不移动,也会在原位得到一个输出点,所以最后得到的输出尺寸是移动的总步数再加上1。
池化
池化的意义在于特征降维,池化技术大大降低了对于计算资源的损耗,除此以外还有降低模型过拟合的优点。池化的思想来源于图像特征聚合统计,通俗理解就是池化虽然会使得图像变得模糊但不影响图像的辨认跟位置判断;池化还有一个优点就是平移不变性,即如果物体在图像中发生一个较小的平移(不超过感受野),那么这样的位移并不会影像池化的效果,从而不会对模型的特征图提取发生影响。
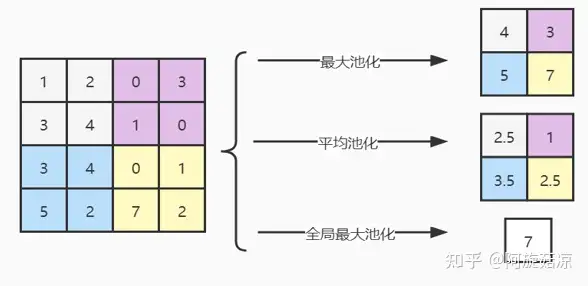
常用的池化方式有3种:最大池化(max pooling)、均值池化(mean pooling)和全局最大池化。
a) 最大池化计算pooling窗口内的最大值,并将这个最大值作为该位置的值;
b) 平均池化计算pooling窗口内的平均值,并将这个值作为该位置的值;
c) 全局最大(平均)池化是计算整个特征图内的最大值(平均值)。
使用池化不会造成数据矩阵深度的改变,只会在高度和宽带上降低,达到降维的目的。3种池化方式描述如图(pooling窗口为2×2)。 其中平均池化能够很好的保留整体数据的特征,能突出背景信息;最大池化能更好的保留纹理上的特征。