坑:
-
补所有题目的代码:口胡的正确性应该都没问题,关键是如何实现得优美一点常数比较小
能过。 -
【Ynoi2015】盼君勿忘 末尾处的复杂度证明。
-
树上分块章节。
-
【Ynoi2006】rsrams 的更优秀做法。
-
矩乘规约章节中的部分证明。
-
大分块章节。(巨坑)
本文大量参考了:
- 《根号数据结构》,成都七中 nzhtl1477,由 dqstz 稍作修改(也感谢他的答疑/bx)
- 《浅谈矩乘规约》,Ynoi 的洛谷博客
本篇内容属于是能看懂但不会用(太菜了
莫队
简单莫队算法
理想莫队信息:维护一个子集的信息,支持 \(O(a)\) 插入一个元素,\(O(b)\) 删除一个元素,无法比直接暴力更高效地合并。
复杂度分析:设块长为 \(B\)。左端点移动的次数为 \(O(n+mB)\),右端点移动次数为 \(O(\frac{n}{B}n)\),总移动次数为 \(O(mB+\frac{n^2}{B})\),取 \(B=\frac{n}{\sqrt m}\) 最优,得到 \(O(n\sqrt m)\)。
一些补充:
-
有没有更优的端点移动方法?
考虑把询问 \((l,r)\) 放在二维平面上,然后找这些点的曼哈顿距离最小生成树。
设树的总边长为 \(d\),那么最优转移的移动次数至少为 \(d\),而按照曼哈顿距离最小生成树转移的移动次数至多为 \(2d\),也就是说,生成树做法的复杂度是与最优转移同阶的。
而可以证明,生成树做法和刚刚说的排序算法的最坏复杂度是同阶的,所以莫队问题可以直接按块排序。
-
奇偶排序(\(l\) 所在块奇偶性不同时,\(r\) 的移动方向也不同,这样减少了 \(r\) 的无效移动)可以快 1/3。
-
调块大小可以快 1/10。
-
更快的排序:直接按 \(r\) 桶排,再按 \(l\) 塞进每个块的 vector 里。
-
由于有 \(O(n\sqrt m)\) 次端点移动和 \(O(m)\) 次询问,所以维护区间信息时可以考虑修改时间较小、查询时间较大的数据结构。
【BZOJ3920】Yuuna 的礼物
题意:
给定一个长度为 \(n\) 的序列 \(a\),每次查询区间中出现次数 k1 小的所有数中权值 k2 小的数。
卡空间。
题解:
考虑莫队。使用 \(O(1)\) 修改,\(O(\sqrt n)\) 查询的数据结构,可以找出第 k1 小的出现次数。
然后对每个出现次数维护权值第 k2 小的数。仍然考虑用 \(O(1)\) 修改 \(O(\sqrt n)\) 查询的数据结构。
但对每个出现次数都开这么一个数组的话空间会爆炸。
但出现次数可能达到 \(x\) 的数也就这么多,我们将它们存下来后离散化。
这样空间是多少?发现就是所有数的出现次数和,即为 \(n\)。
那么就可以做到线性空间。
【Ynoi2015】盼君勿忘
题意:
给定一个长度为 \(n\) 的序列 \(a\),每次查询区间 \([l,r]\) 中所有 \(2^{r-l+1}\) 个子序列的权值和,一个子序列的权值定义为其中出现过的所有数的和(重复出现只算一次),每次询问模数不一样。
\(n,m\leq 10^5\)。
题解:
考虑一个区间 \([l,r]\) 新加入一个数 \(x\) 后产生的贡献,即 \(x\cdot 2^{(r-l+1)-cnt_x}\)。那么如果模数一样的话已经可以直接莫队了。
模数不一样怎么办?首先我们不要考虑一个区间新加入一个数的贡献了,而是直接考虑某个区间的答案。对于区间中每个出现过的数 \(x\),其贡献为 \(x(2^{len}-2^{len-cnt_x})\)。
于是,我们为每个 \(2\) 的幂记录其系数(系数是 \(O(n\cdot a_i)\) 级别的),而有系数的 \(2\) 的幂至多有 \(O(\sqrt n)\) 个(等价于不同的 \(cnt_x\) 的种类数),然后询问的时候找出这些系数非零的 \(2\) 的幂进行计算。
如何找?相当于支持插入、删除、遍历集合中所有数。搞个双向链表即可(插入的时候在链表尾部插入并记录编号,删除的时候按照编号直接在链表中删除)。
还有一个问题是如何计算 \(2\) 的幂?一种方法是注意到 \(2\) 的幂次都 \(\leq n\),所以可以每次询问都 \(O(\sqrt n)\) 预处理光速幂。
另一种方法是,我们要计算的幂次为 \(\{cnt_x\}\),将它们从小到大排序后,考虑依次推过来。于是相当于有 \(k\) 个幂次 \(c_1,\cdots,c_k\),满足 \(c_i<c_{i+1}\) 且 \(\sum_{i=1}^k c_i\leq n\),时间为 \(\sum_{i=1}^k \log(c_i-c_{i-1})=\sum_{i=1}^k \log \Delta_i=\log(\prod_{i=1}^{k}\Delta_i)\),而 \(\sum_{i=1}^k i\Delta_i\leq n\)。根据均值不等式 \(\frac{\sum x_i}{n}\geq \sqrt[n]{\prod x_i}\) 可知:
\[\frac nk\geq \frac{\sum_{i=1}^k i\Delta_i}{k}\geq \sqrt[k]{\prod_{i=1}^k i\Delta_i}\\ \prod_{i=1}^k \Delta_i\leq \frac{\left(\frac{n}{k}\right)^k}{k!}\\ \log(\prod_{i=1}^k\Delta_i)\leq k(\log n-\log k)-(\log 1+\cdots+\log k) \]//咕。最后能证明出来这种方法时间也是对的
莫队二次离线
将莫队过程看成是 \(O(n\sqrt m)\) 次查询区间中的特定信息(即每次询问会带变量)。
在信息具有可减性的前提下,可以差分,变成 \(O(n\sqrt m)\) 次查询前缀的特定信息。
那么原本 \(O(n\sqrt m)\) 次的端点移动,就变成 \(O(n)\) 次的端点移动,尽管查询次数仍然是 \(O(n\sqrt m)\) 次的。
那么此时把根号平衡向插入的方向移动,即插入的时间可以较大,从而降低查询时的时间。
这里要将整个莫队移动的过程离线下来,空间可能会达到 \(O(n\sqrt m)\)。但实际上,以 \(r\) 端点右移为例,发现只有两种情况:
- 用 \(a_{r+1}\) 查询前缀 \(a_{1..r}\)。这种情况本质上只有 \(O(n)\) 种。
- 用 \(a_i,a_{i+1}\cdots,a_j\) 查询前缀 \(a_{1..x}\)。这种情况可以在 \(x\) 处 push 一个 pair 代表区间。
那么空间就降至线性。
树上莫队
查询链的信息:直接利用括号序,每次扫到一个点时,根据该点是否在区间内判断是加入还是删除,注意并不需要差分成到根的路径。
回滚莫队
又称只增(只删)莫队,只需支持增加(删除)和撤销。
回滚莫队在一定程度上和静态分块等价(撒若干个关键点分块,对每一段连续的块预处理答案,然后查询的时候散块暴力加入/删除),但是不需要支持可持久化。
【P5386】【Cnoi2019】数字游戏
题面:
给定一个长度为 \(n\) 的排列,每次查询区间 \([l,r]\) 中有多少子区间的值都在 \([x,y]\) 内。
\(n,m\leq 2\times 10^5\)。
题解:
把 \([l,r]\) 内值在 \([x,y]\) 内的位置都染上黑色,相当于询问所有极长黑色段长度的平方和。
考虑在值域上跑只增莫队,相当于要支持 \(O(n\sqrt m)\) 次染黑(和撤销),以及 \(O(m)\) 次询问序列一个区间所有极长黑色段的平方和。
考虑线段树的做法,每个节点需要维护三个数:答案、左侧极长黑色段长度、右侧极长黑色段长度。
现在考虑在序列上分块,然后对每个块都维护这三个数,查询的时候可以 \(O(\sqrt n)\) 查询。
给一个位置染上黑色,相当于删除和添加 \(O(1)\) 个黑色段,我们只需要找出这些黑色段是啥,就能 \(O(1)\) 在对应的块修改。
发现只需对黑色段的两端 \(l,r\) 维护 \(side_l=r\) 和 \(side_r=l\) 表示另一侧的位置即可维护。
序列分块
通过预处理信息来达到更好的复杂度。
动态分块:带修改。静态分块:不带修改。
静态分块功能为莫队算法的子集,也就是说除非强制在线,不然静态分块一定不如莫队。
强制在线区间众数
考虑到一个性质:对于可重集 \(A,B\),\(A\cup B\) 的众数只可能是 \(A\) 的众数或 \(B\) 中的数。
那么考虑预处理出每一段连续的块的众数,然后询问的时候,只需再对散块的 \(O(\sqrt n)\) 个数查询它们的出现次数即可。
区间出现次数可以考虑用主席树维护。但留意到有 \(O(n)\) 次插入和 \(O(m\sqrt n)\) 次查询,所以考虑将主席树变成如下结构,就能实现 \(O(\sqrt n)\) 插入和 \(O(1)\) 查询:
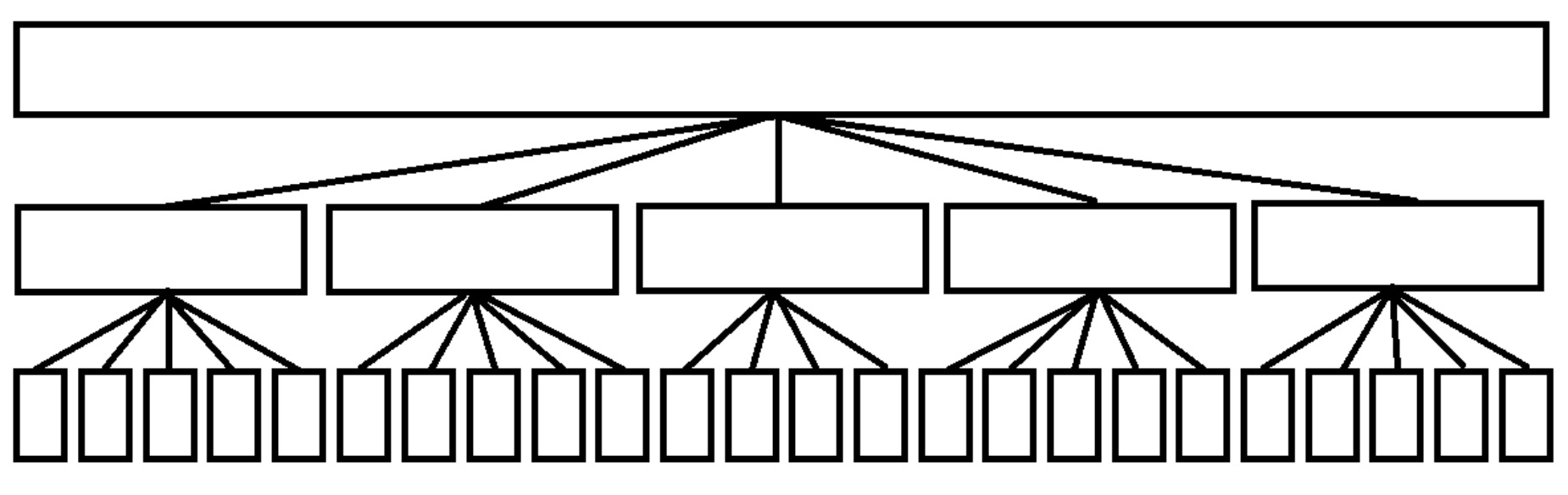
但这样空间是 \(O(n\sqrt n)\) 的。
有一种更很巧妙的线性空间做法:对每个值开个 vector,并存在每个位置在 vector 中的位置。查询的时候同样枚举散块中的数判断是否是众数,先从左往右枚举左散块中的数 \(x\),假设 \(x\) 是第一次被枚举到,那么它是该区间中最左侧的 \(x\),假设当前答案为 \(y\),那么我们可以直接在 vector 中找出 \(x\) 下 \(y\) 次出现的位置,并根据它是否在区间内决定是否要增大 \(y\),若要增大则暴力增大,容易证明 \(y\) 至多增大 \(O(\sqrt n)\)。对于右散块类似处理。
强制在线区间逆序对
同样考虑预处理每一段连续的块的答案。设 \(g(l,r)\) 表示第 \(l\) 个块和第 \(r(l<r)\) 个块之间的配对的贡献,这可以用归并排序 \(O(\sqrt n)\) 求出,然后设 \(f(l,r)\) 表示第 \(l\sim r\) 个块的答案,那么 \(f(l,r)=f(l+1,r)+f(l,r-1)-f(l+1,r+1)+g(l,r)\)。预处理复杂度 \(O(n\sqrt n)\),能解决红色部分。
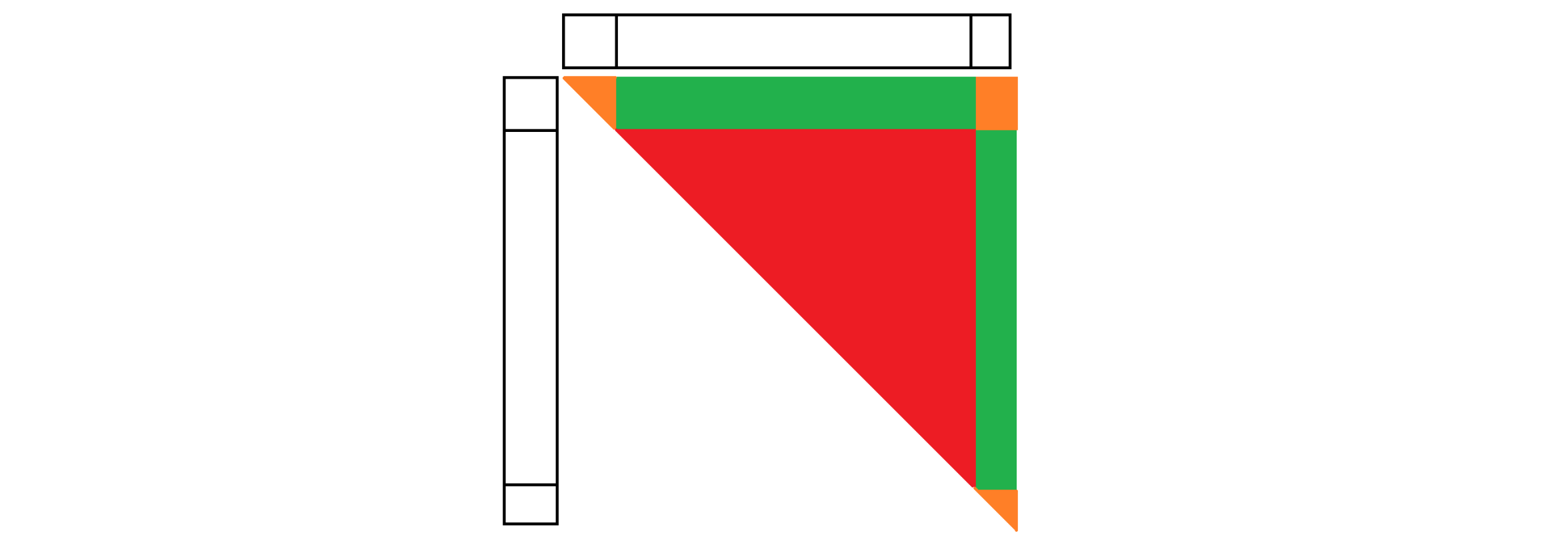
对于绿色部分,差分后变成一段整块前缀和散块的配对,且散块和整块前缀之间有严格的位置关系,而注意到本质不同的可能询问至多 \(O(n\sqrt n)\) 种,那么就容易处理了。
对于边角的橙色部分,考虑预处理处 \(h(l,r)\) 表示区间 \([l,r]\) 的答案,其中 \(l,r\) 在同一块内,方法和 \(f\) 相同。时间复杂度 \(O(n\sqrt n)\)。(注意边角的橙色部分本质上不止 \(O(n)\) 种,因为有可能整个询问都在块内)
对于右上角的橙色部分,它们有严格的位置关系,使用归并排序即可单次询问 \(O(\sqrt n)\) 处理。
时间复杂度 \(O((n+m)\sqrt n)\),常数较大。
多区间合并
题意:
给定一个序列,多次查询区间半群信息,例如 \(\max\)(这里 sb 了,用笛卡尔树就能做到 \(O(n)-O(1)\))。
题解:
假设预处理复杂度为 \(O(n\cdot f(n,k))\),查询的时候合并 \(k\) 次,共 \(k+1\) 个区间的信息。
-
\(k=0\):\(f(n,0)=n\),预处理出所有区间的答案。
-
\(k=1\):\(f(n,1)=\log n\),分治树/猫树,有时也可以用 RMQ 实现。
-
\(k=2\):\(f(n,2)=\log \log n\),sqrt tree。
考虑将长度为 \(n\) 的序列分成 \(O(\sqrt n)\) 块,每块预处理前缀/后缀 \(\max\),并预处理每一段连续的块的 \(\max\)。这样预处理时间是 \(O(n)\) 的。
当询问的区间跨越至少一个块时,就能 \(O(1)\) 求出答案;当询问的区间被某个块完全包含怎么办?
考虑递归地进行下去:对每个长度为 \(k\) 的块再分成 \(O(\sqrt k)\) 个块,然后同样 \(O(k)\) 预处理那些信息,并再递归下去。
这样形成一棵树,而任意询问区间必能被树上的某个节点所恰好包含(即能通过该节点预处理的信息 \(O(1)\) 得到答案)。
考虑这棵树的高度,即 \(\sqrt{\sqrt{\cdots\sqrt n}}\) 的最多层数:观察到 \((((2^2)^2)\cdots)^2\),其中上标共有 \(k\) 个 \(2\),即树高为 \(k\) 层,其大小为 \(2^{2^k}\),所以树高为 \(O(\log\log n)\)。
那么,我们就能通过 \(O(n\log \log n)\) 的建树,使得每次询问只用合并 \(3\) 个区间的信息。
具体实现上,如何找出刚刚说的询问区间恰好被树上哪个节点所包含呢?
考虑先将初始的 \(n\) 钦定为 \(2\) 的幂 \(n=2^k\),然后分块的时候采用 \(2^{\lfloor k/2\rfloor}\) 的块大小,这样能保证每层的块大小都是同一个 \(2\) 的幂。
那么假设这一层的块大小都是 \(2^{k}\),那么这一层每个块对应的区间就是 \([0,2^k),[2^k,2\times 2^k),[2\times 2^k,3\times 2^k),\cdots\)。从而,若 \([l,r]\) 被其中某个块完全包含,只需保证 \(l,r\) 的第 \(k\) 位及以上完全相同。
在所有层对应的块大小 \(2^{k_1}>2^{k_2}>2^{k_3}>\cdots\) 中,我们仅需找出最小的 \(k_i\),使得 \(l,r\) 的第 \(k\) 位及以上完全相同。
那么仅需找出 \(l\oplus r\) 的最高位即可,这个可以预处理或者用库函数。
上面的猫树如果也想 \(O(1)\) 找到对应节点,应该也要用类似技巧。
-
……
更多跟这个问题有关的,自行见 https://www.luogu.com.cn/problem/P6020。
根号分治
【Ynoi2015】此时此刻的光辉
题意:
给定一个序列 \(a\),多次查询一个区间乘积的约数个数。
\(n,m\leq 10^5\),\(a_i\leq 10^9\)。
题解:
对每个数分解质因数后,考虑用莫队来做,朴素的话是 \(O(n\sqrt m\cdot \omega(V))\),其中 \(\omega(V)\) 在 \(10\) 左右。
考虑降低移动端点的复杂度,而升高询问的复杂度。可以根号分治:端点移动的时候只考虑 \(>V^{1/3}\) 的质数幂次变化,这样端点移动是 \(O(1)\) 的;而询问的时候将 \(\leq V^{1/3}\) 的所有质数都扫一遍,用前缀和直接求出区间内的幂次和。
复杂度 \(O(nV^{1/4}+m\frac{V^{1/3}}{\log V}+n\sqrt m)\)。其中 \(O(nV^{1/4})\) 是 Pollard-Rho 分解质因数的时间。
根号重构
对时间分块。
带 link,cut 树上路径点权 kth
考虑每 \(B\) 个操作重构一次。
假设当前要重构,那么我先把接下来 \(B\) 次操作涉及到的 cut 的边先从当前图中忽略,然后得到若干个连通块。
那么接下来 \(B\) 次操作中的某次询问的路径,就对应着 \(O(B)\) 个连通块上的路径的并。
那么重构的时候对每个连通块都维护主席树,查询的时候就能用 \(O(B)\) 棵主席树的加减得到路径并对应的主席树了。
找出是哪些连通块的路径并可能要用 LCT。
时间复杂度 \(O(\frac{m}{B}n\log n+mB\log n)\),取 \(B=\sqrt n\) 得 \(O(m\sqrt n\log n)\)。
【Ynoi2006】rprmq2
题意:
平面上矩形加,查询矩形最大值。
\(m\leq 2\times 10^5\)。
题解:
先顺便证一下 KDT 的复杂度(
首先,若 KDT 当前节点范围内有 \(n\) 个点,那么该子树的树高是 \(O(\log n)\) 的。
-
若要修改的矩形与当前节点对应的矩形有三条边重合,那么该节点的两个儿子的各两个儿子,共 4 个节点中,容易观察到只有 2 个节点需要递归下去,且递归下去后要修改的矩形仍然满足有三条边重合的条件。于是至少两层分支数才会翻倍,最后的分支数是 \(O(2^{\log n/2})=O(\sqrt n)\)。于是该情况的时间复杂度为 \(O(\sqrt n)\)。
-
若要修改的矩形与当前节点对应的矩形有两条相邻边重合。仍然考虑 4 个 “儿子的儿子”,它们中有至多一个仍然是两条边重合,其他会有至多两个变成三条边重合(即第一种情况),那么 \(T(n)=T(n/4)+2\cdot O(\sqrt{n/4})+O(1)\),得到 \(T(n)=O(\sqrt n)\)。
-
若要修改的矩形与当前节点对应的矩形有两条对边重合。仍然考虑 4 个 “儿子的儿子”,发现 \(T(n)=\max(2T(n/4),T(n/4)+2O(\sqrt{n/4}),4O(\sqrt{n/4}))\),得到 \(T(n)=O(\sqrt n)\)。
-
若要修改的矩形与当前节点对应的矩形有一条边重合。仍然考虑 4 个 “儿子的儿子”,发现 \(T(n)=\max(T(n/4)+2O(\sqrt{n/4}),4O(\sqrt{n/4}))\),得到 \(T(n)=O(\sqrt n)\)。
-
若要修改的矩形与当前节点对应的矩形没有边重合。仍然考虑 4 个 “儿子的儿子”,发现 \(T(n)=\max(T(n/4),4O(\sqrt{n/4}))\),得到 \(T(n)=O(\sqrt n)\)。
(上面的记号使用不严谨,但证明是没问题的)
那么对于这一题来说,使用 KDT 我们就能得到一个 \(O(m^2)\) 的做法。
考虑每 \(B\) 个操作分一块。根据块内的 \(B\) 个操作将平面划分为 \(B\times B\) 的网格,然后在这个网格上使用刚刚说的算法,只需 \(O(B^2)\)。
现在问题是如何预处理出这 \(B\times B\) 的网格每个格子的初始权值。即 \(O(m)\) 次矩形加后 \(O(B^2)\) 次矩形求和,且这 \(O(B^2)\) 个矩形构成网格。可以差分后用历史版本和线段树 \(O((m+B^2)\log m)\) 解决。注意到每次询问都是同样的 \(B\) 个区间,于是通过对线段树做一些扭曲,并做一些预处理,就能使得每个询问区间恰好对应线段树上一个节点且每次询问恰好能 \(O(B)\) 完成。
这样总复杂度将至 \(O(\frac{m}{B}(m\log m+B^2))\),取 \(B=\sqrt{m\log m}\) 得到 \(O(m\sqrt{m\log m})\)。
树上分块
咕。
例题
Trick1 Pair 贡献
贡献形如:
- 区间内所有 \(i<j\) 满足 \(a_i=a_j\)。
- 区间内所有 \(i<j\) 满足 \(a_i+a_j=c\)(\(a_i\oplus a_j=c\)),\(c\) 为不随询问改变的常数。
- 区间内所有 \(i<j\) 满足 \(a_i>a_j\)。
之类。
一种方法是分块,预处理块对块的贡献,典型例子是强制在线区间逆序对。
另一种方法是对出现次数根号分治。
【Ynoi ?】TEST_93
题意:
给定一棵 \(n\) 个点的数,每次查询给定 \(k\) 个点,求其虚树上任意两条边,边权相等的方案数。
\(n,m,\sum k\leq 10^5\)。
题解:
先对每种边权的出现次数根号分治。
对于出现次数 \(>\sqrt n\) 的边权,每种能够 \(O(m)\) 处理对询问的贡献。
对于出现次数 \(\leq \sqrt n\) 的边权,枚举每种可能的 pair,发现它们有贡献当且仅当虚树在两个 dfn 区间中都存在点。
一个暴力的想法是找出虚树的所有叶子,并每两两询问,这样变成了 \(O(n\sqrt n)\) 次矩形加和 \(O(\sum k^2)\) 次单点查询。
再考虑对 \(k\) 根号分治,若 \(k\leq \sqrt n\),我们仍然使用上述算法,若 \(k>\sqrt n\) 我们直接暴力 \(O(n)\) 跑一遍得到答案。
平衡一下可以得到一个 \(O(n\sqrt{n\log n})\) 的算法。
N/A
题意:
给你一个长度为 \(n\) 的序列 \(a\) 和常数 \(k\),并且有同样长度为 \(n\) 的序列 \(b\) 初始为 \(0\)。
多次给出 \(l,r,w\),对所有 \(l\leq i<j\leq r\) 且 \(a_i\oplus a_j=k\) 的 \((i,j)\) 执行 b[i]+=w,b[j]-=w。
最后输出序列 \(b\)。
题解:
不妨以计算 b[j]-=w 的贡献为例。
考虑如下暴力:离线扫序列,若遇到一个 \((l,r,w)\) 的 \(l\),则将 \(i\in [l,r]\) 的所有 c[i]+=w,若遇到一个 \((l,r,w)\) 的 \(r\),则将 \(i\in[l,r]\) 的所有 c[i]-=w,每次扫到 \(j\) 的时候询问 \(i\in [1,j]\) 中所有 \(a_i=a_j\oplus k\) 的 c[i] 的和即为 b[j] 的减少量。
根据 \(a_i\) 的出现次数根号分治:对于出现次数 \(\leq \sqrt n\) 的 \(a_i\),每次 \(j\) 询问时直接暴力扫一遍它们的位置并查询,于是需要支持 \(O(m)\) 次区间加和 \(O(n\sqrt n)\) 次单点查询,使用 \(O(\sqrt n)\) 修改 \(O(1)\) 查询的数据结构即可;对于出现次数 \(>\sqrt n\) 的 \(a_i\),我们每个单独处理,每种可以通过小改一下上面的暴力过程(\(j\) 边移边记录当前前缀中 c[i] 的和)做到单次 \(O(n)\)。
时间复杂度 \(O((n+m)\sqrt n)\)。
Trick2 带区间染色的分块
可以序列分块,然后对每个块特判其是否为同色块,在这个基础上再用颜色段均摊。
【JRKSJ R3】practiceZ
题意:
给定长度为 \(n\) 的序列 \(a,b\),要求支持操作:
- 区间 \(a\) 置为 \(x\)。
- 区间 \(b\) 置为 \(x\)。
- 求 \(\sum_{i=l}^rs_{b_i}\),其中 \(s\) 表示 \(a\) 的前缀和。
\(n\leq 5\times 10^5\)。认为 \(n,m\) 同阶。
题解:
考虑颜色段均摊搭配差分,将操作 1 转化成二元组 \((r,x)\),意为 \(a\) 前缀加 \(x\),那么对 \(s_{b_i}\) 的影响就是 \(s_{b_i}\gets s_{b_i}+x\min(b_i,r)\)。那么就算没有 2 操作,怎么看也不能 polylog 了。
考虑对 \(b\) 序列分块,并维护每个块的答案。对 \(a\) 进行 \((r,x)\) 修改的时候,块的答案的变化为 \(\sum_{i=bl}^{br}x\min(b_i,r)\),那么考虑用数据结构维护该块内 \(b_i\) 在值域上的前缀和信息,即可通过查询得到答案的变化。
如果没有 2 操作,搭配 \(a\) 的 \(O(\sqrt n)\) 修改 \(O(1)\) 查询前缀和,已经能在 \(O(n\sqrt n)\) 的复杂度解决问题了。
现在考虑回 2 操作。当对整块进行操作时可以直接打标记。对散块进行操作时,更新答案可以直接暴力询问 \(a\) 的前缀和,但还要修改块内 \(b_i\) 在值域上的数据结构。发现利用了颜色段均摊后,只剩下总共 \(O(n)\) 次的单点修改。那么使用 \(O(\sqrt n)\) 修改 \(O(1)\) 查询的数据结构即可。
总时间复杂度 \(O(n\sqrt n)\)。线性空间需要对每块离线处理,而且应该需要实现技巧。
【JRKSJ R?】r?srcyffffn!s
题意:
给定长度为 \(n\) 的序列 \(a\),和长度为 \(m\) 的集合序列 \(S\),初始 \(S_i\) 均为空集,要求支持操作:
- \(S_k\gets S_k\cup [l,r]\)。
- 查询 \(a_l,\cdots,a_r\) 中在 \(S_k\) 中的数的个数。
\(n,m,q\leq 10^5\)。
题解:
首先通过均摊的方法,容易保证第一种操作中 \([l,r]\) 与 \(S_k\) 不交。
not very hard 的分块做法:
考虑对 \(a\) 分块,修改的时候更新每个块对 \(S_k\) 的答案,询问的时候对散块需要知道某个 \(a_i\) 是否在 \(S_k\) 中,容易 \(O(\sqrt n)\) 修改和 \(O(1)\) 查询。总复杂度 \(O(n\sqrt n)\)。通过离线逐块处理容易做到线性空间。
hard 的根号分治做法:
考虑对集合的操作次数根号分治。若一个集合的操作次数 \(>\sqrt n\),则显然有 \(O(n)\) 的均摊方法(需要 \(O(1)\) 修改 \(O(\sqrt n)\) 查询);若一个集合的操作次数 \(\leq \sqrt n\),可以直接暴力遍历之前的每次操作并求出贡献,那么相当于 \(O(n)\) 个点和 \(O(m\sqrt n)\) 次矩形数点,使用 \(O(\sqrt n)\) 修改 \(O(1)\) 查询即可。
Trick3 块的笛卡尔积
如果询问区间 pair 贡献信息,因为信息可拆分,可以对序列分块,然后预处理块对块的贡献,这里就是块的笛卡尔积。询问时需要高效处理单点对块区间贡献(一般可以差分成单点对块前缀贡献),单点对单点贡献(这里一般对两个零散块暴力处理得到),块之间的贡献即上述的块对块二维数组的矩形信息合并。
典型例子是强制在线区间逆序对。
【Ynoi ?】TEST_92
题意:
区间内点对树上最近距离。
题解:
知道了思路之后,效仿强制在线区间逆序对的做法即可。
- 块区间:转化为单块对单块。枚举第一个块,然后多源 bfs 求出到每个点的最短路,即可得到所有第二个块的答案。
- 散块对块区间:转化为单块对散块。和第一种情况的处理方法相同。
- 块内部区间:转化为块内单点对单点。先求出整个块的虚树,然后暴力在虚树上跑出两两点对距离。
- 散块对散块:考虑询问时合并两个散块建出虚树再求。需要预先对块内点按 dfn 排序,然后需要 \(O(1)\) lca。
时间复杂度 \(O(n\sqrt n)\)。
【Ynoi2010】Brodal queue
题意:
长度为 \(n\) 的序列 \(a\),要求支持:
- 区间染色
- 区间选出两个数相等的方案数。
\(n\leq 2\times 10^5\)。认为 \(n,m\) 同阶。
题解:
分块,容易 \(O(n\sqrt n)\) 实时维护每种数的前缀出现次数。
计算区间每种数出现次数的平方和,尝试利用 \((a-b)^2=a^2-2ab+b^2\) 转为维护 \(f(i,j)(i<j)\) 表示每种数 \(\text{前 }i\text{ 个块出现次数}\times \text{前 }j\text{ 个块出现次数}\) 之和。
考虑当第 \(k\) 个块颜色 \(c\) 的出现次数变化 \(x\) 后,如何更新 \(f(i,j)\),设 \(c\) 在前 \(i\) 个块中出现了 \(a\) 次,在前 \(j\) 个块中出现了 \(b\) 次。
- 若 \(i<k\leq j\),那么增加了 \(a(b+x)-ab=f(i,j)+ax\),这相当于进行第 \(i\) 行后缀加。
- 若 \(k\leq i<j\),那么增加了 \((a+x)(b+x)-ab=ax+bx+x^2\),这相当于进行第 \(i\) 行整体加和第 \(j\) 列后缀加。
- 若 \(i<j\leq k\),没有变化。
从而,当一个块变化后,我们能 \(O(\sqrt n)\) 修改 \(f\),\(O(\sqrt n)\) 单点查询 \(f\)。
但一次修改可能会对 \(O(\sqrt n)\) 个块修改,怎么办?
当一个块只有一种颜色时,考虑不把它统计进 \(f\),而在询问的时候单独计算(这样询问的时候需要另加计算的只有至多 \(O(\sqrt n)\) 种颜色,这是可以接受的),这样要修改次数是均摊 \(O(n)\) 的。
时间复杂度 \(O(n\sqrt n)\)。
Trick4 莫队+bitset
【Ynoi2016】掉进兔子洞
题意:
给定一个长度为 \(n\) 的序列 \(a\)。记函数 \(f(x,l,r)\) 表示 \(x\) 在 \(a_l,\cdots,a_r\) 中出现的次数。
每次给出 \(k\) 个区间 \([l_1,r_1],\cdots,[l_k,r_k]\),求 \(\sum_{x}\min\{f(x,l_i,r_i)\}_{i=1}^k\)。
\(n,\sum k \leq 10^5\)。
题解:
先离散化,假设数 \(x\) 离散化后的位置是 \(y\),出现了 \(z\) 次。那么让 \(x\) 占用位置 \([y,y+z)\)。莫队维护区间 bitset 时,假设 \(x\) 出现了 \(w\) 次,那么我们把 \([y,y+w)\) 置为 1,把 \([y+w,y+z)\) 置为 0。然后每个区间的 bitset 取 and 再 count 就是答案。
时间复杂度 \(O(n\sqrt m+\frac{nm}{w})\),其中 \(m=\sum k\)。
Trick5 常数维满点集正交范围加和的根号平衡
考虑如下的分块算法, 来支持平面上的单点修改和 2-side 矩形求和操作。
考虑设置值 \(B,k\),并假设 \(n=B^k\)。我们将平面不断按 \(B\times B\) 的形状分块,共分 \(k\) 层。
考虑询问的时候,我们这么处理:
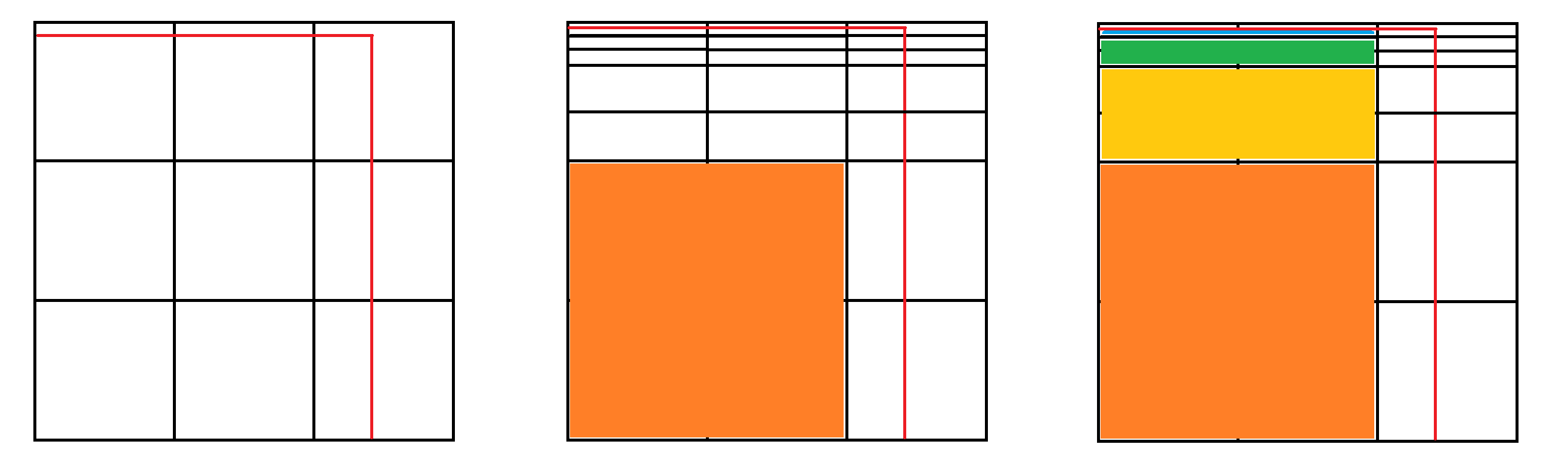
如左图,假设要询问的是红线框出的 2-side 矩形,注意这里的黑线代表的是第一层的分块而非每个格子(即可以认为 \(B=3\))。
查询的时候,我们先调用维护了的这一层的二维前缀和(如何维护在修改部分讲,下同),即橙色部分。然后考虑其正上方的部分,先递归 \(k\) 层,分别调用黄色、绿色、蓝色部分……。然后对于正右方的部分也同理维护。对于剩下右上角的部分递归到其所在的块。那么查询的复杂度是 \(O(k^2)\) 的。
对于修改来说,考虑如何更新当前层的信息。首先我们要更新二维前缀和(对应查询时的橙色部分),这是 \(O(B^2)\) 的。然后更新查询时对应的黄色、绿色、蓝色部分,这需要另递归 \(k\) 层处理,每层需要 \(O(B^2)\) 的时间。于是一层需要 \(O(kB^2)\) 的时间,每层都要这样更新一下,共 \(O(k^2B^2)\) 的时间。
空间上,当 \(k\) 太大时,需要使用动态开点。
用 \(n\) 来表示的话,修改是 \(O(B^2\log_B^2n)\) 的,询问是 \(O(\log_B^2n)\) 的。可以看出几点:
- 当 \(B=2\) 时,修改、查询复杂度均为 \(O(\log^2 n)\),这符合我们的预期(和树套树同复杂度)。
- 若修改次数和查询次数同阶,则在 \(B=e\) 时取到最优。
- 取 \(B=n^{1/4}\),即可常数较小地做到 \(O(\sqrt n)\) 修改和 \(O(1)\) 查询。
同样地,反演(差分)一下也容易做到 \(O(\log_B^2 n)\) 修改 \(O(B^2\log_B^2n)\) 查询。
貌似任意常数维的情况都能类似处理,做到类似 \(O(\sqrt n)\) 修改和 \(O(1)\) 查询。
【Ynoi2007】rdiq
题意:
给定一个长度为 \(n\) 的序列。每次给出 \(l,r\),询问集合 \(\{(a_i,a_j):l\leq i<j\leq r\land a_i>a_j\}\) 的大小。
\(n\leq 10^5\),\(m\leq 5\times 10^5\)。
题解:
当 \(a_i\) 两两不同时为区间逆序对,那么考虑莫队。
以 \(r\) 右移为例,记 \(a_r\) 上一次出现的位置为 \(r'\),那么我们要统计的是 \(r'<i<r\),\(a_i\) 未在 \(a_l,\cdots,a_{r'}\) 中出现,且 \(a_i>a_r\) 的 \(i\) 的数量。
考虑二次离线下来后对 \(l\) 从大往小扫,那么为保证 \(a_i\) 未在 \(a_l,\cdots,a_{r'}\) 中出现,对于同样的权值我们只保留离 \(l\) 最近的那个,然后询问就相当于询问 \((r',r)\) 内 \(>a_r\) 的被保留的数的个数。
那么相当于平面上有 \(O(n)\) 次单点修改和 \(O(n\sqrt m)\) 次矩形查询。那么最后可以做到 \(O(n\sqrt n+n\sqrt m)\)。
【Ynoi2077】3dmq
题意:
三维空间上有 \(n\) 个点,每个点有点权 \(a,b\),给定 \(a\),初始 \(b\) 为 \(0\)。要求支持操作:
- 对 \(x\leq X,y\leq Y,z\leq Z\) 的点进行 \(b\gets b +a w\)。
- 询问 \(x\leq X,y\leq Y,z\leq Z\) 的点的 \(b\) 的和。
\(n,m\leq 5\times 10^5\)。
题解:
考虑每 \(O(\sqrt m)\) 次重构。需要解决两个问题:重构和 \(O(\sqrt m)\) 个询问的维护。
每次重构后维护好所有点的权值,那么新的一次重构相当于新加入 \(O(\sqrt m)\) 次三维空间加,以及最后 \(O(n)\) 次单点查询,即一个 \(O(\sqrt m)-O(n)\) 的三维数点问题(\(O(A)-O(B)\) 分别表示点数和询问数,通过反演等方式它们是可以交换的)。
如何维护每两次重构间的 \(O(\sqrt m)\) 次询问。把询问的贡献分成两部分,一部分是重构前的修改的贡献,由于我们已经维护了所有点的权值,所以这相当于一个 \(O(n)-O(\sqrt m)\) 的三维数点问题;一部分是重构后的修改的贡献,考虑一次修改 \((X_1,Y_1,Z_1)\) 对 \((X_2,Y_2,Z_2)\) 的贡献,那么相当于询问 \(x\leq \min(X_1,X_2),y\leq \min(Y_1,Y_2),z\leq \min(Z_1,Z_2)\) 的 \(a\) 权和,那么这相当于一个 \(O(n)-O(\sqrt m^2)\) 的三维数点问题,但注意这里前面的 \(O(n)\) 是仅跟 \(a\) 权有关的,所以不需每次重构。
那么现在要解决的是:
- \(O(\sqrt m)\) 次 \(O(\sqrt m)-O(n)\) 的三维数点。
- \(O(\sqrt m)\) 次 \(O(n)-O(\sqrt m)\) 的三维数点。
- 一次 \(O(n)-O(m\sqrt m)\) 的三维数点。
三维数点可以以先对一维扫描线,另两维要维护的是动态单点加和矩形查,使用恰当的均衡即可做到 \(O(n\sqrt n)\) 的(视 \(n,m\) 同阶)。
Trick6 逐块处理
用来卡空间,常数上也会改进。一般每个块的询问的贡献独立。
Trick7 分块后分治
【Ynoi2013】D2T2
题意:
给定一个长度为 \(n\) 的序列,每次给出 \(l,r,L,R\),查询将序列中值在 \([L,R]\) 内的位置保留不变,其他位置变为 0 后,序列中 \([l,r]\) 的最大子段和。
\(n,m\leq 10^5\)。
题解:
全局查询我们有一种如下做法:考虑对于一个长度为 \(k\) 的区间,离散化后本质不同的询问只有 \(O(k^2)\) 种。那么考虑分治合并每种询问的答案,每次合并利用归并就能做到 \(O(k^2)\),时间复杂度 \(T(n)=2T(n/2)+O(n^2)\),得 \(T(n)=O(n^2)\)。
对于原问题我们考虑分块,每块内通过上述方式 \(O(\sqrt n^2)=O(n)\) 处理出对该块每种本质不同的询问的答案,然后询问的时候再合并 \(O(\sqrt n)\) 个块的信息即可。
时间复杂度 \(O((n+m)\sqrt n)\)。
其他例题
【Ynoi2006】rsrams
题意:
给定长度为 \(n\) 的序列 \(a\),多次查询一个区间内所有子区间的绝对众数的和。
绝对众数定义为出现次数*2大于等于区间长度。
\(n,m\leq 10^6\)。
题解:
考虑对某种颜色 \(c\) 计算其贡献。记 \(b_i=\begin{cases}1&a_i=c\\-1&a_i\neq c\end{cases}\),那么一段区间 \([l,r]\) 有贡献当且仅当 \(\sum_{i=l}^rb_i\geq 0\)。
我们考虑如下过程:从左往右扫描序列 \(b\),如果扫到了一个 \(1\),先将其标记,然后找到其左边的最近的未被标记的 \(-1\)(如果存在)并将其标记。
然后我们断言,被标记的位置恰是所有可能的 \(l\) 端点。证明如下:考虑将扫描时标记的 \(1\) 当作右括号,\(-1\) 当作左括号,那么被标记的极长段每段都是一个括号序列,且除了处在序列前缀的那一段(如果存在),其他段都是合法括号序列,且处在序列前缀的那一段抵消之后肯定只剩下若干个右括号。现在考虑选任意一个未被标记的位置作为 \(l\),首先该位置肯定是 \(-1\),且该位置之后的所有括号极长段每段都是合法括号序列,从而考虑 \(r\) 从 \(l\) 开始一直移动到 \(n\) 的过程,发现 \(\sum_{i=l}^rb_i\) 初始等于 \(-1\),且过程中 \([l,r]\) 内左括号的数量一定一直不小于右括号的数量(因为途经的每段都是合法括号序列),从而过程中始终保持 \(\sum_{i=l}^rb_i<0\),那么不可能存在一个以该 \(l\) 开头的合法区间。同理,容易看出,以任意一个被标记的位置开头,都一定存在至少一个合法区间。
同理从右往左扫一遍序列 \(b\) 也可得到所有 \(r\) 的可能位置。从而我们找到了所有端点的可能位置,而它们不超过 \(O(k)\) 个,其中 \(k\) 为 \(1\) 的个数,即 \(c\) 的出现次数。
由于 \(\sum_{i=l}^rb_i\geq 0\) 可以转化成 \(pre_r-pre_{l-1}\geq 0\),那么一次询问就相当于区间逆序对。于是考虑直接在这 \(O(k)\) 个有用的点拼成的序列上跑莫队,时间复杂度可以做到 \(O(m+k\sqrt m)\)(需要二次离线)。
然后考虑根号分治,对于出现次数 \(>\sqrt n\) 的颜色,我们考虑使用上述算法;对于出现次数 \(\leq \sqrt n\) 的颜色,考虑直接将 \(O(\sqrt n^2)=O(n)\) 个有用的 pair 找出来,然后转为 \(O(n\sqrt n)-O(m)\) 的二维数点问题,直接维护即可。
时间复杂度 \(O(n\sqrt n)\),视 \(n,m\) 同阶。
//PPT 里有一手 \(O(n\sqrt m+m\log n+n^{1+\varepsilon})\) 的做法(这个做法估计才用到了分块后分治),没太懂里面的结论,先咕着
【JRKSJ R2】你的名字。
题意:
给定长度为 \(n\) 的序列 \(a\),多次查询区间模 \(k\) 意义下最小值。
\(n,m\leq 3\times 10^5\),\(a_i,k\leq 10^5\)。
题解:
对 \(k\) 根号分治,若 \(k\leq \sqrt v\) 则暴力处理,使用 \(O(n)\) 预处理 \(O(\sqrt v)\) 查询区间 \(\min\) 的数据结构即可。
若 \(k>\sqrt v\),先分块,散块我们暴力处理,然后转化为 \(O(\sqrt v)\) 次查询区间 \(\geq x\) 的最小的数,且区间一定是一段连续的块。
离线下来后,相当于在一个长度为 \(O(\sqrt n)\) 的序列上,进行过 \(O(n)\) 次单点修改和 \(O(m\sqrt v)\) 次查询区间 \(\min\)。这里考虑使用如下的数据结构:建立该序列的猫树,在猫树的每个节点处维护前缀/后缀 \(\min\) 就能 \(O(1)\) 查询(这里可以直接暴力把每个询问对应猫树哪个节点预处理出来),且一次修改的时间为 \(O(\sqrt n+\sqrt n/2+\sqrt n/4+\cdots)=O(\sqrt n)\)。
时间复杂度 \(O(n(\sqrt n+\sqrt v))\),视 \(n,m\) 同阶。
【Ynoi2007】rfplca
题意:
给定长度为 \(n-1\) 的序列 \(f\),保证 \(f_i<i\),则它表示一棵树。要求支持操作:
- 区间 \(f\) 减 \(x\)。
- 查询两点 lca。
\(n,m\leq 4\times 10^5\)。
题解:
考虑分块,维护每个点第一次跳出块外时跳到的节点 \(jp_i\)。
散块修改时暴力重构,但整块修改时发现好像不太好 \(O(1)\) 做。
这里需要注意到一个整块修改 \(O(\sqrt n)\) 次后一定有 \(f_i\) 在块外,即 \(jp_i=f_i\),那么之后的修改都可以通过打标记的方式进行。之前的修改仍然暴力重构,这部分时间是 \(O(n\sqrt n)\) 的。
询问的时候先一块一块地 \(O(\sqrt n)\) 跳到某个公共祖先,然后回退一块,再一步一步地 \(O(\sqrt n)\) 跳到 lca。
【Ynoi2008】rsmemq
题意:
给定长度为 \(n\) 的序列 \(a\)。多次查询一个区间内有多少长度为奇数的子区间 \([l,r]\) 使得值 \((l+r)/2\) 为该区间的众数(出现次数 \(=\max\) 即可,多个最多的也算)。
\(n,m\leq 5\times 10^5\)。
题解:
枚举值 \(x\),设 \(x\) 总共出现了 \(k\) 次。考虑寻找 \(x\) 为众数的合法区间。合法区间一定以某个中心 \(mid\) 对称,考虑从 \(mid\) 往外扩展,\(x\) 在区间中的出现次数有至多 \(O(k)\) 种,每种里面,\(x\) 出现次数固定时,我们希望通过找到一组合法的区间,它们形如 \([mid-i,mid+i]\)(\(l\leq i\leq r\))。暴力二分的话相当于 \(O(n\log n)\) 次在线区间众数的询问,这样复杂度不优。
正解是根号分治,对于 \(k>\sqrt n\) 的数我们直接暴力扫所有以 \(mid\) 为中心的区间;对于 \(k\leq\sqrt n\),我们只需考虑众数出现次数 \(\leq \sqrt n\) 的区间。考虑将 \(mid\) 右移,并对每个 \(j\) 维护使得 \([mid-i,mid+i]\) 众数出现次数为 \(j\) 的最小的 \(i\),然后和 \(mid\) 处的询问归并,移动的时候对每个 \(j\) 暴力 \(O(1)\) 改即可。
这样我们在 \(O(n\sqrt n)\) 的时间内找到了所有合法区间组。
然后原问题转化为如图的数点问题:有 \(O(n)\) 条红色线段,\(O(m)\) 次询问绿框内的线段长度和。
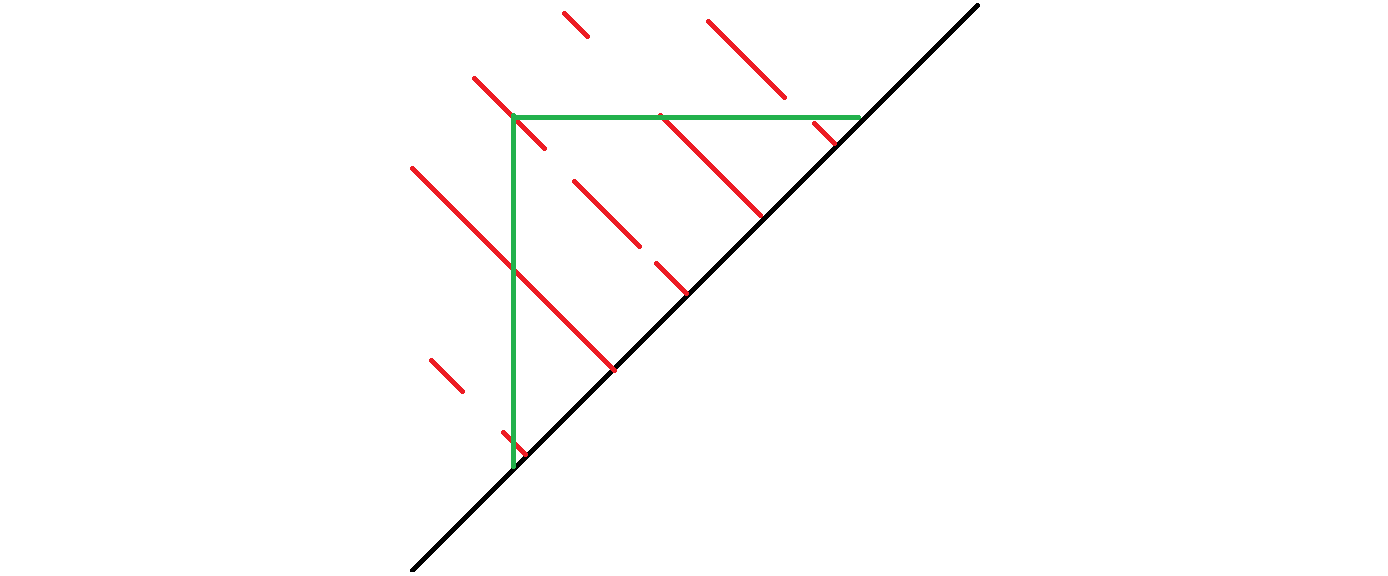
这个和【Ynoi2010】Self Adjusting Top Tree 同样的套路。最后时间复杂度 \(O(n\sqrt n+m\log n)\)。
【CF840E】In a Trap
题意:
给定一棵 \(n\) 的点的树,每个点 \(i\) 有点权 \(a_i\)。每次给出 \(u,v\),保证 \(u\) 为 \(v\) 的祖先,查询 \(\max_{i\in\operatorname{path}(u,v)}a_i\oplus dis(i,v)\)。
\(n,a_i<2^{16}=65536\),\(m\leq 10^5\)。
题解:
考虑这么一个问题:有一个序列 \(a\),每次给出 \(x\),询问 \(\max a_i\oplus (i+x)\)。
考虑将询问的区间分成极长的若干块,使得块内 \(i+x\) 的第 \(B\) 位以上都是相同的(现将低 \(B\) 位称为低位,第 \(B\) 位以上称为高位),这样会有至多两个散块,且中间的每块都长为 \(2^B\)、且该块内的 \(i+x\) 的低位在 \([0,2^B)\) 内依次遍历。
对于某一块内,由于 \(i+x\) 高位都是一样的,所以我们就先找使得高位异或值最大的那些 \(a_i\),它们的高位也应是一样的,然后我们找到它们中 \(a_i\oplus (i+x)\) 低位最大的。
那么考虑对每个可能的块(共 \(O(n)\) 个)预处理数组 \(g_{y}\),表示只考虑该块内高位等于 \(y\) 的那些 \(a_i\),它们 \(a_i\oplus (i+x)\) 低位最大是多少。预处理该数组能直接 \(O(n2^B)\) 解决。
询问的时候,散块暴力 \(O(2^B)\) 扫一遍,然后枚举共 \(O(n/2^B)\) 个整块,每个整块中找到使得高位异或值最大的那些 \(a_i\) 对应的同一个 \(y\),然后查询 \(g_y\)。
如何找到该 \(y\)?可以预先对每个可能的块内的 \(y\) 建 01Trie,然后在 01Trie 上查。
时间复杂度 \(O(n2^B\log V+m(2^B+\frac{n}{2^B}\log V))\),取 \(2^B=O(\sqrt n)\) 得 \(O((n+m)\sqrt n\log v)\)。
这里的 01Trie 可以用压位 Trie 实现,每个点有 16 个儿子(每 4 位压一段)。需要快速知道当儿子集合为 \(S\)、询问为 \(x\) 时,这 4 位哪个儿子异或 \(x\) 最大,这需要 \(O(16\times 2^{16})\) 的时间预处理。但这样好像只有除 4 的常数(
这一题由于值域和 \(n\) 同级,所以块内可以直接统一对每种 \(x\) 的高位预处理出对应的 \(y\),做到 \(O((n+m)\sqrt n)\)。实现需要比较精细。
【Ynoi2077】stdmxeypz
题意:
给定一棵大小为 \(n\) 的有根树,要求支持操作:
- 给出 \(a,x,y,z\),将 \(a\) 子树内距离 \(a\) 模 \(x\) 等于 \(y\) 的节点的点权加上 \(z\)。
- 查询某节点的点权。
\(n,m\leq 3\times 10^5\)。
题解:
考虑根号分治。
若 \(x>\sqrt n\),那么将每层的节点按 dfn 排好序后,一次询问相当于对 \(O(\sqrt n)\) 个区间进行区间加,可以使用 \(O(1)\) 修改 \(O(\sqrt n)\) 查询。关键在于如何定位区间。
问题转变为求 \(a\) 的 \(k\) 级后代中 dfn 最小(最大)的点。一种做法是将询问离线后长剖合并儿子维护的数组,但这样空间复杂度是 \(O(m\sqrt n)\) 的,为降至线性,我们可以考虑根号重构,即每 \(\sqrt m\) 个询问就跑一遍离线长剖。
另一种方法是,考虑另建一棵森林 \(T_L\),\(x\) 的父亲为 \(y\) 当且仅当 \(d_y=d_x+1\),\(\mathrm{dfn}_x<\mathrm{dfn}_y\) 且 \(\mathrm{dfn}_y\) 最小。容易看出,\(a\) 的在 \(T_L\) 上的 \(k\) 级祖先就是我们要找的那个点,用长剖可以 \(O(1)\) 查询。
若 \(x\leq \sqrt n\),那么对每种 \(x\) 单独考虑。将所有节点、属于该 \(x\) 的所有修改、和所有询问都按模 \(x\) 的余数划分,每个划分类中就是子树加和单点查,用 \(O(\sqrt n)\) 修改 \(O(1)\) 查询即可。
时间复杂度 \(O((n+m)\sqrt n)\)。
【Ynoi2013】文化课
题意:
有数字序列 \(\{a_1,\cdots,a_n\}\) 和运算符序列 \(\{p_1,\cdots,p_{n-1}\}\),其中运算符是加法或乘法。要求支持操作:
- 区间 \(a\) 置为 \(x\)。
- 区间 \(p\) 置为 \(x\)。
- 询问 \(a_l\ p_l\ \cdots\ p_{r-1}\ a_r\) 的结果模 \(10^9+7\)。
\(n,m\leq 10^5\)。
题解:
将序列拆成极长乘法段。考虑用线段树维护,一个区间只需维护:中间的极长乘法段的和,以及两侧的极长乘法段。
关键在于区间置 \(a\) 的修改,设修改的区间中间的极长乘法段(不含两侧)分别为 \(c_1,\cdots,c_k\),那么我们要快速计算 \(\sum_{i=1}^k x^{c_i}\)。这里注意到 \(\sum c_i\leq n\),所以至多有 \(O(\sqrt n)\) 种不同的 \(c_i\),假设我们知道了有序的每种出现的 \(c_i\) 以及它们的出现次数,我们就能 \(O(\sqrt n)\) 计算出答案(快速幂的分析类似于之前的某题)。
现在考虑如何记录区间有序的每种出现的 \(c_i\)。合并两个区间可以使用归并,中间的 \(O(1)\) 段需要单独处理。而修改 2 后得到区间的 \(c_i\) 是 \(O(1)\) 的。
这样的时间为 \(T(n)=T(n/2)+O(\sqrt n)=O(\sqrt n)\),空间为 \(T(n)=2T(n/2)+O(\sqrt n)=O(n)\)。
【CF700D】Huffman Coding on Segment
题意:
给一个长度为 \(n\) 的序列,每次询问一个区间内的数进行最小二进制编码后的总长(哈夫曼编码)。
相当于把每个数的出现次数扔进一个堆里,每次取出最小的两个 \(a,b\) 合并成 \(a+b\),让答案加上 \(a+b\),再将 \(a+b\) 扔进堆中。
\(n,m\leq 10^5\)。
题解:
先考虑一个技巧:假设给出的所有数都是排序好的,那么构建它们的哈夫曼树可以做到线性。具体实现是发现每次重新扔进堆中的数一定是不降的,所以用两个队列来模拟堆,一个队列存原来给你的数,一个队列存重新扔进堆中的数。
然后考虑用莫队维护区间每种数的出现次数,注意这样的出现次数只会有 \(O(\sqrt n)\) 种,那么我们再对每种出现次数维护其出现次数,而且维护的是有序的(即维护出 \(O(\sqrt n)\) 个二元组 \((p_i,q_i)\),满足 \(p_i<p_{i+1}\),且出现了 \(p_i\) 次的数恰有 \(q_i\) 种)。端点移动的过程中,相当于要给某个位置减一,并给它的一个相邻位置加一,然后用链表维护所有非零位置即可。
现在考虑对这 \(O(\sqrt n)\) 个 \((p_i,q_i)\) 求哈夫曼树。每次取出最小的 \((p_i,q_i)\),考虑直接批处理这 \(q_i\) 个 \(p_i\),即往堆中(这里只是抽象意义,具体还是用双队列实现)插入 \((2p_i,\lfloor q_i/2\rfloor)\),然后可能单独剩下一个 \(p_i\) 在下一轮特殊考虑一下。
考虑这样做的时间复杂度,由于实现的时候可以保证队列中相邻两个 pair 的 \(p_i\) 不同,且每次扔进堆里的数都严格变大,所以进行 \(O(\sqrt n)\) 轮后,两个队列中的最小值都已经 \(>\sqrt n\),而 \(\sum p_iq_i\) 是不变的,于是至多有 \(O(\sqrt n)\) 种 \(p_i\),即堆中至多只有 \(O(\sqrt n)\) 个数,那么至多再会有 \(O(\sqrt n)\) 次合并就结束。
时间复杂度 \(O(n\sqrt n)\),视 \(n,m\) 同阶。
矩阵乘法相关规约
若能将 B 问题转化为 A 问题,即 B 问题是 A 问题的一种情况(子集),那么称 A 问题是不弱于 B 问题的,此时解决 A 问题的最优时间复杂度不低于解决 B 问题的最优时间复杂度。
很多分块题是不弱于 \(\sqrt n\times \sqrt n\) 大小的矩阵乘法的。
而目前矩阵乘法的上界只做到了 \(O(n^{2.373})\),所以如果做这类题目的时间复杂度是无法低于 \(O(\sqrt n^{2.373})\) 的,而且一般来说时间复杂度也不应该低于普通的矩乘 \(O(\sqrt n^3)=O(n\sqrt n)\)(否则相当于把矩乘的科技套到了具体题目上)。这有助于我们分析题目的复杂度下界。
具体来说,这里的矩阵乘法包含:
- 整数矩阵乘法:相乘的矩阵的元素为某范围 \([0,n]\) 中的整数(需满足 \(n\geq 1\))。
- 01 矩阵乘法:相乘的矩阵的元素 \(\in \{0,1\}\)。
- bool matrix mul:\(C_{i,j}=\operatorname{OR}_{k}A_{i,k}\&B_{k,j}\)。
- max-plus 矩阵乘法:\(C_{i,j}=\max_k A_{i,k}+B_{k,j}\)。
- 注意矩阵自乘是不弱于普通矩乘的:考虑普通矩乘,把两个相乘的矩阵放在一个大矩阵里并对角连接,就变成了矩阵自乘。
现在我们来证明一些问题是不弱于 \(\sqrt n\times \sqrt n\) 大小的矩阵乘法的,我们只需把任意矩阵乘法规约到要证的问题即可(这是单向规约),或证明要证的问题等价于任意矩阵乘法(这是双向规约)。
一般来说,为证明双向规约,我们可以先证明单向规约,再通过给出和矩乘相同复杂度的做法得到双向规约。
区间每个数出现次数平方和
将平方的含义理解为:区间中任意选两个 \(i,j\),统计 \([a_i=a_j]\) 的和。
将序列分成 \(O(\sqrt n)\) 个块。
考虑大小为 \(O(\sqrt n)\times O(\sqrt n)\) 的 01 矩阵 \(A\),用 \(A_{i,j}\) 表示第 \(i\) 块是否包含数 \(j\)。
考虑 \(B=A^2\),那么 \(B_{i,j}\) 的含义就是第 \(i\) 块配对第 \(j\) 块的贡献。
设 \(Q_{l,r}\) 表示询问第 \(l\) 块到第 \(r\) 块的答案。那么 \(Q_{l,r}=\sum_{i=l}^r\sum_{j=l}^rB_{i,j}\),反演一下得到 \(B_{i,j}=Q_{l,r}-Q_{l+1,r}-Q_{l,r-1}+Q_{l+1,r-1}\)。
于是知道 \(Q\) 后就能 \(O(n)\) 求 \(B\),那么在询问数与序列长度同级的情况下,原问题不弱于 \(O(\sqrt n)\times O(\sqrt n)\) 的矩阵乘法。
区间逆序对
考虑将序列反过来后,再对同样的询问区间做一次。这样我们通过常数轮(两轮)区间逆序对就知道了每个区间的顺序对数和逆序对数,那么就能求出每个区间的相等对数,等价于区间每个数出现次数平方和。所以区间逆序对不弱于区间每个数出现次数平方和。
x加y和
x加y和:\(n\times n\) 的网格平面上有 \(n\) 个点,要求支持 \(x<A\) 加、\(y<B\) 和。
考虑用x加y和做区间出现次数平方和。
先将 \((i,a_i)\) 放在平面上,将 \(r\) 从左往右扫。\(r\) 右移时,将 \(y<a_r\) 的点加;询问时查询 \(x<r+1\) 的点和减 \(x<l\) 的点和,得到的就是 \((l,r)\) 中 \(a_i\neq a_j\) 的 \((i,j)\) 数量,再减一下就能得到 \(a_i=a_j\) 的 \((i,j)\) 数量,即区间出现次数平方和。
所以x加y和不弱于区间出现次数平方和。
行加列和
行加列和:\(n\times n\) 的网格平面上有 \(n\) 个点,要求支持 \(x=A\) 加、\(y=B\) 和。
考虑行加列和的最优复杂度是 \(A(n)\),x加y和的最优复杂度是 \(B(n)\)。
考虑将网格平面依次按 \(1\times 1\) 大小的格子(原始网格平面)、\(2\times 2\) 大小的格子、\(4\times 4\) 大小的格子……,来划分。
这样通过类似倍增的方式,一次 \(x<A\) 加可以恰好变为在这 \(O(\log n)\) 个网格平面每个上的 \(O(1)\) 次行加,\(y<B\) 和也可以恰好变为在这 \(O(\log n)\) 个网格平面每个上的 \(O(1)\) 次列加。
这个算法做x加y和的复杂度为 \(A(n)O(\log n)\)(注意不是 \(A(n)+A(n/2)+\cdots\),因为 \(O(\frac{n}{2^k})\times O(\frac{n}{2^k})\) 大小的网格平面中不一定只有 \(O(\frac n{2^k})\) 个格子有值,所以此时正确的操作是仍然是在 \(n\times n\) 的网格平面上进行,唯一不同的就是将 \(2^k\times 2^k\) 区块内的所有点都归一地缩到同一个点上去,再做行加列和)。那么应有 \(B(n)\leq A(n)O(\log n)\),从而 \(A(n)\geq \frac{B(n)}{O(\log n)}\)。这个结论对于我们分析问题到底是根号的还是 polylog 的已经够了。
单点加一圈和
单点加一圈和:给定一张 \(n\) 个点 \(n\) 条边的图,要求支持单点加、查询相邻节点和。
考虑用单点加一圈和做行加列和。将带 \(n\) 个点的 \(n\times n\) 的网格平面看成是邻接矩阵,然后发现行加列和就是单点加一圈和(把单点加看成是该点的所有有向出边加,一圈和看成是该点的有向入边和)。
矩形加矩形和
不弱于行加列和。
矩形加矩形max
考虑任意两个大小为 \(O(\sqrt n)\times O(\sqrt n)\) 的矩阵 \(A,B\) 进行 max-plus 矩阵乘法得到 \(C\)。
那么 \(C_{i,j}=\max_k A_{i,k}+B_{k,j}\)。那么可以看成是,对 \(B\) 矩阵每行 \(k\) 行加 \(A_{i,k}\) 后,再问每列 \(j\) 的 \(\max\)。
这可以用矩形加矩形max解决,从而矩形加矩形max不弱于 \(O(\sqrt n)\times O(\sqrt n)\) 的 max-plus 矩阵乘法。
矩形取max矩形和
区间众数
lxl 也说看不懂,现在能做到 \(O(n^{1.49})\)。
链颜色数
考虑从根挂下来 \(O(\sqrt n)\) 条链。
考虑大小为 \(O(\sqrt n)\times O(\sqrt n)\) 的 01 矩阵 \(A\),用 \(A_{i,j}\) 表示第 \(i\) 条链是否包含颜色 \(j\)。
考虑 \(B=A^2\),那么 \(B_{i,j}\) 的含义就是 \(i,j\) 两条链共有的颜色数。
这也可以通过询问 \(i,j\) 两条链并的颜色数得到。
那么至少 \(O(n)\) 次询问的链颜色数不弱于 \(O(\sqrt n)\times O(\sqrt n)\) 的矩阵乘法。
区间出现奇数次的数的个数
将序列分成两半,左右各分为 \(O(\sqrt n)\) 块。
考虑任意两个大小为 \(O(\sqrt n)\times O(\sqrt n)\) 的矩阵 \(A,B\)。
考虑用 \(A_{i,j}\) 表示序列左半边后 \(i\) 个块中 \(j\) 的出现次数的奇偶性,\(B_{i,j}\) 表示序列右半边前 \(i\) 个块中 \(j\) 的出现次数的奇偶性。显然每种 \(A,B\) 都是可以构造出对应的序列的。
设 \(C=AB\),那么 \(C_{i,j}\) 表示在左半边后 \(i\) 个块和右半边前 \(j\) 个块都出现了奇数次的颜色个数。
现在通过 \(O(n)\) 次询问,可以知道这个区间内出现偶数次的颜色个数,即 \((K-A)(K-B)+AB\),其中 \(K\) 为全 \(1\) 矩阵。
拆开得到 \(K^2-KB-AK+2AB\),而 \(K^2,KB,AK\) 都是能 \(O(\sqrt n^2)=O(n)\) 求出的,那么就能解出 \(AB\)。也就是说我们能将原问题以 \(O(n)\) 的额外时间代价规约到 \(O(\sqrt n)\times O(\sqrt n)\) 的矩阵乘法,于是原问题不弱于 \(O(\sqrt n)\times O(\sqrt n)\) 的矩阵乘法。
区间相同数间的最大距离
/*
将序列分成两半,左右各分 \(O(\sqrt n)\) 块。
考虑任意两个大小为 \(O(\sqrt n)\times O(\sqrt n)\)、值域为 \(O(\sqrt n)\) 的矩阵 \(A,B\) 进行 max-plus 矩阵乘法得到 \(C\)。
*/
区间加,区间 \(\leq x\) 的数的个数
将序列分成 \(O(\sqrt n)\) 块。
考虑任意两个大小为 \(O(\sqrt n)\times O(\sqrt n)\) 的 01 矩阵 \(A,B\)。
用 \(B_{i,j}\) 表示初始时序列第 \(i\) 块是否包含 \(j\)。
将操作每 \(O(\sqrt n)\) 个分一组,用 \(A_{i,j}\) 表示第 \(i\) 组操作后,第 \(j\) 块是否是原来 \(+n\)。
设 \(C=AB\),那么 \(C_{i,j}=\sum_{k} A_{i,k}B_{k,j}\) 的组合意义为:枚举每个块 \(k\),然后统计 “第 \(i\) 组操作后这块是原来 \(+n\)” 且 “这块中原来包含 \(j\)” 的块数。
那么 \(C_{i,j}\) 即为第 \(i\) 组操作后全局 \(=n+j\) 的数的个数,那么用两次询问相减即可问出。
容易发现总操作数和总询问数都是 \(O(n)\) 次的,于是在这个前提下,原问题不弱于 \(O(\sqrt n)\times O(\sqrt n)\) 的矩阵乘法。
区间加,区间 kth
考虑 “区间加,区间 kth” 的最优复杂度为 \(A(n)\),“区间加,区间 \(\leq x\)” 的最优复杂度为 \(B(n)\)。显然,我们能用前者套整体二分对后者问题做到 \(A(n)O(\log n)\) 的复杂度,那么有 \(B(n)\leq A(n)O(\log n)\),从而 \(A(n)\geq \frac{B(n)}{O(\log n)}\)。
标签:复杂度,sqrt,查询,leq,区间,数据结构,询问,根号 From: https://www.cnblogs.com/ez-lcw/p/16975574.html