一、二维树状数组
二维树状数组,其实就是一维的树状数组上的节点再套个树状数组,就变成了二维树状数组了。
const int N = 1e3 + 10;
int tr[N][N], n, m;
#define lowbit(x) (x & -x)
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
tr[i][j] += d;
}
int query(int x, int y) {
int ret = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
ret += tr[i][j];
return ret;
}
二、单点修改,区间查询
给出一个 \(n × m\) 的零矩阵 \(A\) ,你需要完成如下操作:
- \(1\) \(x\) \(y\) \(k\) :表示元素 \(A\)_{\(x\) , \(y\)} 自增 \(k\)
- \(2\) \(a\) \(b\) \(c\) \(d\): 表示询问左上角为 \((a,b)\) ,右下角为 \((c,d)\) 的子矩阵内所有数的和

单点增加,因此可以直接加上就可以了
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 5000; // 2^(12)=4096
int n, m;
LL tr[N][N];
#define lowbit(x) (x & -x)
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
tr[i][j] += d;
}
LL query(int x, int y) {
LL ret = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
ret += tr[i][j];
return ret;
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> m;
int opt;
while (cin >> opt) {
if (opt == 1) {
int x, y, d;
cin >> x >> y >> d;
add(x, y, d);
} else {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1) << '\n';
}
}
return 0;
}
三、区间修改,单点查询
给出一个 \(n × m\) 的零矩阵 \(A\) ,你需要完成如下操作:
- \(1 \, a \, b \, c \, d \, k\):表示左上角为 \((a,b)\) ,右下角为 \((c,d)\) 的子矩阵内所有数都自增加 \(k\);
- \(2 \, x \, y\) :表示询问元素 \(A_{x,y}\) 的值。
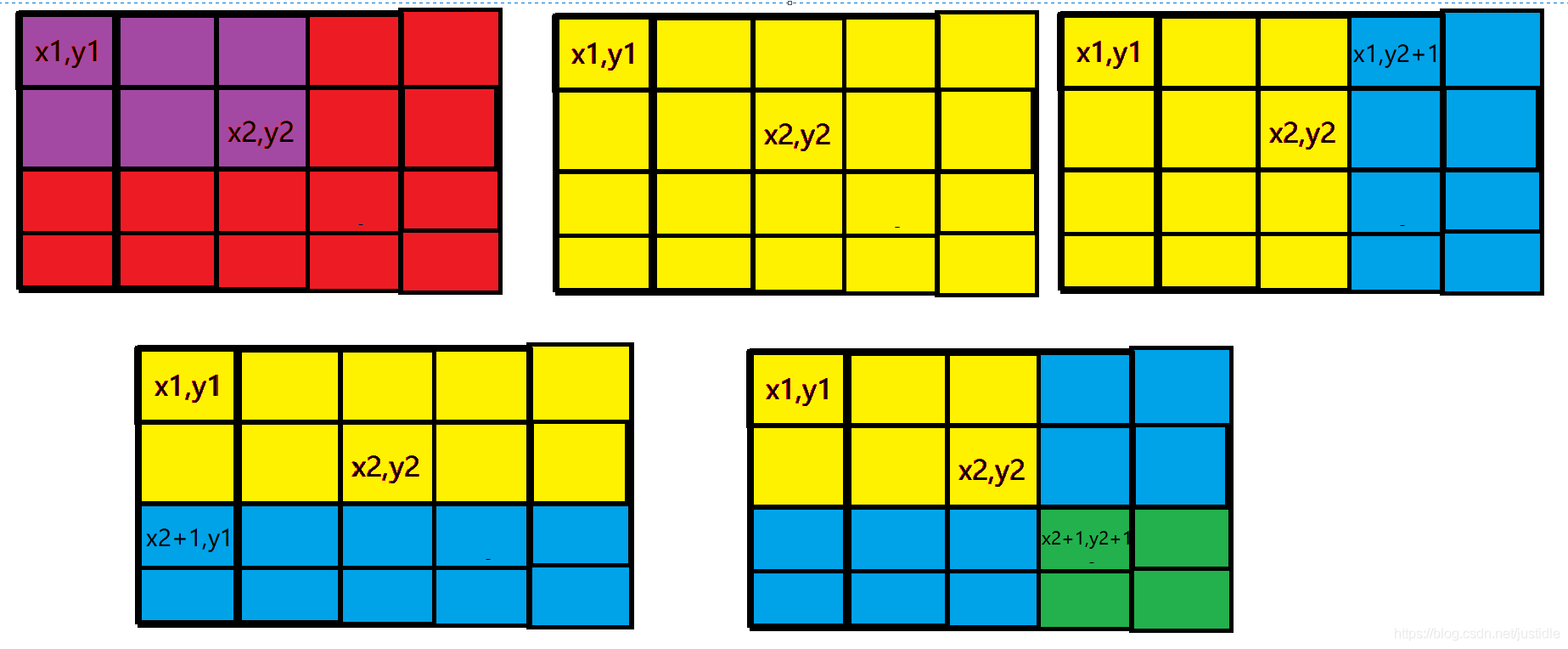
只需要利用一个二维树状数组,维护一个二维差分数组,单点查询即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 5000;
int bit[N][N];
int n, m;
LL tr[N][N];
#define lowbit(x) (x & -x)
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
tr[i][j] += d;
}
LL query(int x, int y) {
LL ret = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
ret += tr[i][j];
return ret;
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> m;
int op;
while (cin >> op) {
if (op == 1) {
int x1, y1, x2, y2, d;
cin >> x1 >> y1 >> x2 >> y2 >> d;
//二维差分
add(x1, y1, d);
add(x1, y2 + 1, -d);
add(x2 + 1, y1, -d);
add(x2 + 1, y2 + 1, d);
} else {
int x, y;
cin >> x >> y;
cout << query(x, y) << '\n';
}
}
return 0;
}
四、区间修改,区间查询
给定一个大小为 \(N × M\) 的零矩阵,直到输入文件结束,你需要进行若干个操作,操作有两类:
-
\(1 \, a\, b\, c\, d\, x\),表示将左上角为 \((a,b)\) ,右下角为 \((c,d)\) 的子矩阵全部加上 \(x\);
-
\(2\, a\, b\, c\, d\,\) , 表示询问左上角为 \((a,b)\) ,右下角为 \((c,d)\) 为顶点的子矩阵的所有数字之和。
考虑前缀和 \(\large S_{x,y}\) 和原数组 \(a\) 和差分数组 \(b\) 的关系。
\(\large \displaystyle S_{x,y}=\sum_{i=1}^x\sum_{j=1}^ya_{i,j} \\ \,\, \,\, \,\, \,\, \,\, \, =\sum_{i=1}^x\sum_{j=1}^y\sum_{k=1}^i\sum_{l=1}^jb_{k,l} \\ \,\, \,\, \,\, \,\, \,\, \, = \sum_{i=1}^x\sum_{j=1}^y[xy-y(i-1)-x(j-1)+(i-1)(j-1)]b_{i,j} \\ \,\, \,\, \,\, \,\, \,\, \, = xy\sum_{i=1}^x\sum_{j=1^y}b_{i,j}-y\sum_{i=1}^x\sum_{j=1}^y(i-1)b_{i,j}-x\sum_{i=1}^x\sum_{j=1}^y(j-1)b_{i,j}+\sum_{i=1}^x\sum_{j=1}^y(i-1)(j-1)b_{i,j} \)
为什么可以推导出这样的公式?考虑单个位置 \((x,y)\) 与 \(b_{i,j}\):
\([xy-y(i-1)-x(j-1)+(i-1)(j-1)]b_{i,j}\)(利用容斥原理),所以将每个位置加起来,就是\(s_{x,y}\)。因此,我们只需要维护四个树状数组,分别维护\(b_{i,j},(i-1)b_{i,j},(j-1)b_{i,j},(i-1)(j-1)b_{i,j}\),就可以了。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2050;
int n, m;
LL a[N][N], b[N][N], c[N][N], d[N][N];
#define lowbit(x) (x & -x)
void add(int x, int y, int v) {
for (int i = x; i <= n; i += lowbit(i)) {
for (int j = y; j <= m; j += lowbit(j)) {
a[i][j] += v;
b[i][j] += (x - 1) * v;
c[i][j] += (y - 1) * v;
d[i][j] += (x - 1) * (y - 1) * v;
}
}
}
LL query(int x, int y) {
LL ret = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
ret += x * y * a[i][j] - y * b[i][j] - x * c[i][j] + d[i][j];
return ret;
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> m;
int opt;
while (cin >> opt) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
if (opt == 1) {
int v;
cin >> v;
add(x1, y1, v);
add(x1, y2 + 1, -v);
add(x2 + 1, y1, -v);
add(x2 + 1, y2 + 1, v);
} else
cout << query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1) << '\n';
}
return 0;
}