浅尝 计算图优化&&算子融合
- 激活值做饱和量化，选择合适的阈值
|T| - 权值直接作非饱和量化
What is a Computational Graph - - - 计算图是什么？
- C = {N, E, I, O} 一个计算图，可以表示为由一个节点(Node),边集(Edge),输入边(Input),输出边(Output)组成的四元组。
- 计算图是一个又向联通无环图，其中的节点也被称为算子(Operator)
- 算子必定有边相连，输入边，输出边不为空
- 计算图中可以有重边（两个算子之间可以由两条边相连，PS:这种情况会让解析图的时候遇到一些困难）
operator - - - 算子
- 算子是神经网络的最小调度单位，遗憾的是算子并非原子的：一个复杂的算子可以被更细粒度的算子所表示
如： Gemm = Matmul + Bias
一个 通用矩阵乘算子 ，可以被拆分成一个 普通矩阵乘算子 加上一个 Bias(加法算子) - 算子只能被完整地调度到一个设备上去，不能将算子的一部分调度到CPU上，一部分调度到GPU上去。
针对模型做图优化的两个目的
- 减少计算图中的 node 数量
- 不管是算子融合，还是无效节点去除，共同的目的就是减少整个 graph 中 node 的数量，因为对于框架来说，从一个 node 到另一个 node 之间就意味着数据的搬运。
- 适配硬件的限制
- 对于一些通用硬件来说基本没什么问题，但是有些硬件设备对算子的支持很少，有各种各样的限制。这个时候我们对 计算图 进行优化,将算子转换成硬件支持的算子。
- 最常见的是将各种算子转成卷积，而卷积又可以转换为矩阵相乘，(大多数板子都是支持矩阵运算的)
- PS：有些加速器是没有 直接进行卷积运算 的硬件单元，但是有矩阵相乘的运算单元，那么需要把卷积运算转化成矩阵运算，for example（Im2col）
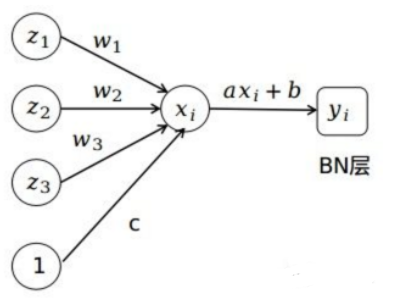
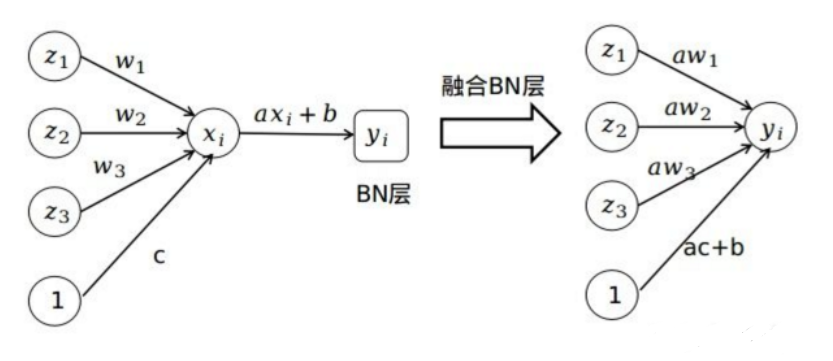
最常见的一个算子融合
conv2d+bn+relu--->fused-conv2d-bn-relu- 训练时 bn 层做了哪些操作？
- 推理时 bn 层做了哪些操作？
- 我们以一个三个输入神经元的全连接网络为例：
用图直观的表示：
- 训练时 bn 层做了哪些操作？
从另外一个角度看算子融合
MatMul+Bias+Relu--->fused_MatMul_Bias_Relu
| // 三重循环做矩阵乘 MatMul | |
| __declspec(noinline) vodi MatMul( | |
| ELEMENT_TYPE** input,ELEMENT_TYPE** weight, | |
| ELEMENT_TYPE** output, const unsigned int num_of_elements){ | |
| for (unsigned int i = 0;i < num_of_elements; i++) | |
| for (unsigned int j = 0; j < num_of_elements; j ++) | |
| for (unsigned int k = 0; k < num_of_elements; k ++) | |
| output[i][j] += input[i][k] * weight[k][j]; | |
| } |
| // 双重循环做两个矩阵相加 Bias | |
| __declspec(noinline) void BiasAdd( | |
| ELEMENT_TYPE** input, ELEMENT_TYPE* bias, | |
| ELEMENT_TYPE** output, const unsigned int num_of_elements){ | |
| for (unsigned int i = 0; i < num_of_elements; i ++) | |
| for (unsigned int j = 0; j < num_of_elements; j ++) | |
| output[i][j] += bias[i]; | |
| } |
| // 二重循环做Relu，将大于零的都保留，小于零的都归零 | |
| __declspec(noinline) void Relu( | |
| ELEMENT_TYPE** input, ELEMENT_TYPE** output, | |
| const unsigned int num_of_elements){ | |
| for (unsigned int i = 0; i < num_of_elements; i ++) | |
| for (unsigned int j = 0; j < num_of_elements; j ++) | |
| output[i][j] = input[i][j] * (input[i][j] > 0) | |
| } |
- 在 Matmul + Bias + Relu 这样一个算子串行结构中，如果不融合算子，output 将至少被写入3次，并且启动三个算子也比较占用时间
- 在图中我们可以看到
- 每一个算子都有四个阶段
- E - - - CPU发射任务阶段
- R - - - 从内存中读取数据阶段
- C - - - 计算算子结果阶段
- W - - - 将算得结果写入内存阶段
- 其中 Bias 和 Relu 算子都是 访存密集型算子，他们在读取和写入数据所耗费的时间要远远大于计算所耗费的时间。
- 每一个算子都有四个阶段
| // 算子融合后 | |
| __declspec(noinline) void Fused_MatMul_Bias_Relu( | |
| ELEMENT_TYPE** input,ELEMENT_TYPE** weight, ELEMENT_TYPE* bias, | |
| ELEMENT_TYPE** output, const unsigned int num_of_elements){ | |
| for (unsigned int i = 0; i < num_of_elements; i ++){ | |
| int accumulator = 0; | |
| for (unsigned int k = 0; k < num_of_elements; k ++){ | |
| accumulator += input[i][k] * weight[k][j]; | |
| } | |
| output[i][j] = accumulator + bias[j] > 0 ? accumulator + bias[j]:0; | |
| } | |
| } |
-
以上代码做了如下的优化：
- 将 bias 作为参数传入融合算子这个函数中
- accumulator 位于寄存器中，最后的 output[i][j] 的值也是在寄存器中做计算的
- 访存次数从 3 ---> 1
-
对这三个算子进行融合
-
这个融合过程将 Bias 和 Relu 算子的 W , E , R 部分都删除了
-
同时将 MatMul、Bias 、Relu 算子的 C 部分融合到了一起
Q.E.D.
赏 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 移动端推理框架 标签：elements,int,unsigned,ELEMENT,浅尝,num,&&,算子 From： https://www.cnblogs.com/sinferwu/p/16930830.html